Numerical Simulation and Control of Satellite Formation Flying with EKF-Based Navigation in MATLAB

Author : Waqas Javaid
Abstract:
Satellite formation flying enables high-resolution space missions through the coordinated operation of multiple spacecraft but requires precise modeling, navigation, and control in a perturbed orbital environment. This study presents an integrated dynamics, estimation, and control framework for autonomous satellite formation flying implemented in MATLAB. The relative motion of deputy spacecraft is modeled using Hill–Clohessy–Wiltshire equations under low-Earth-orbit conditions with realistic perturbation considerations [1]. A Linear Quadratic Regulator provides baseline stabilization, while a Model Predictive Control strategy ensures fuel-optimal trajectory tracking under thruster saturation constraints. An Extended Kalman Filter is employed for onboard state estimation using range and range-rate measurements, accounting for sensor noise and model uncertainty. Numerical integration is performed using a fourth-order Runge–Kutta scheme to propagate nonlinear relative dynamics [2]. Closed-loop performance is evaluated using high-fidelity simulations over multiple orbital periods. Key metrics such as formation error convergence, control effort, and total ΔV consumption are analyzed. Simulation results demonstrate accurate formation maintenance and rapid stabilization under constrained actuation. The proposed framework highlights the effectiveness of combining predictive control and state estimation for autonomous satellite clustering missions. This work provides a validated simulation tool for future research in multi-spacecraft coordination and distributed space systems.
- Introduction:
Satellite formation flying has emerged as a transformational technology for modern space missions that require distributed sensing, interferometry, and high-resolution Earth observation.

- Figure 1: Satellite Formation Flying.
By coordinating the motion of multiple small spacecraft instead of a single large platform, formation flying offers increased mission flexibility, fault tolerance, and cost efficiency.
Table 1: Physical Constants Used in Satellite Formation Dynamics.
Parameter | Value |
Earth Gravitational Parameter μ (m³/s²) | 3.986004418×10^14 |
Earth Radius Re (m) | 6.378137×10^6 |
J2 | 1.08262668×10^-3 |
Orbit Altitude (m) | 700000 |
Maintaining precise relative positioning among satellites is a highly challenging problem due to nonlinear orbital dynamics, environmental perturbations, limited onboard actuation, and noisy sensor measurements [3]. Accurate mathematical modeling of relative orbital motion forms the foundation for designing reliable formation control strategies.
Table 2: Hill–Clohessy–Wiltshire (HCW) State Matrix A.
x | y | z | vx | vy | vz |
0 | 0 | 0 | 1 | 0 | 0 |
0 | 0 | 0 | 0 | 1 | 0 |
0 | 0 | 0 | 0 | 0 | 1 |
3n² | 0 | 0 | 0 | 2n | 0 |
0 | 0 | 0 | -2n | 0 | 0 |
0 | 0 | -n² | 0 | 0 | 0 |
Table 3: HCW Control Input Matrix B.
Row | Col 1 | Col 2 |
1 | 0 | 0 |
2 | 0 | 0 |
3 | 0 | 0 |
4 | 1 | 0 |
5 | 0 | 1 |
6 | 0 | 0 (z-axis thrust) |
The Hill–Clohessy–Wiltshire (HCW) equations are commonly employed to describe linearized relative dynamics about a circular reference orbit, providing a tractable framework for controller synthesis. Traditional linear control techniques, such as the Linear Quadratic Regulator (LQR), offer stability and simplicity but lack the ability to explicitly handle control constraints and fuel optimization requirements. Model Predictive Control (MPC) addresses these limitations by solving a finite-horizon optimal control problem at each time step, enabling constraint enforcement and performance optimization. In parallel, robust navigation algorithms are essential to compensate for modeling errors and sensor noise during formation maintenance [4].

- Figure 2: Satellite Formation Flying Control Center with EKF-Based Navigation.
The Extended Kalman Filter (EKF) remains a widely used estimation technique due to its computational efficiency and capacity to handle nonlinear measurement models. Combining advanced control methods with reliable state estimation enables fully autonomous operation of satellite clusters. Numerical simulation serves as a critical testbed for assessing closed-loop performance prior to on-orbit deployment. MATLAB provides a versatile platform for implementing high-fidelity spacecraft dynamics, estimation algorithms, and optimization-based control techniques. This study integrates these elements into a unified simulation framework for satellite formation flying. The proposed system incorporates linearized relative dynamics, RK4-based numerical propagation, EKF-based navigation, and constrained MPC guidance under thruster saturation limits. Performance metrics, including formation error convergence, navigation accuracy, and total delta-V consumption, are evaluated over extended orbital periods. The effectiveness of the integrated approach is demonstrated through multiple simulation scenarios [5]. The results confirm that predictive control combined with real-time state estimation can achieve accurate, fuel-efficient formation keeping. This research contributes a comprehensive numerical tool for analyzing autonomous multi-satellite coordination problems.
1.1 Background and Motivation:
Satellite formation flying represents a paradigm shift in spacecraft mission design, enabling multiple small satellites to operate cooperatively as a single distributed system. This approach significantly enhances mission capabilities in Earth observation, space-based interferometry, synthetic aperture radar, and astronomy by allowing flexible baselines and reconfigurable sensing geometries. Compared to traditional monolithic satellites, formations offer reduced fabrication cost, higher fault tolerance, and scalability. However, the success of such missions critically depends on maintaining precise relative positions and orientations among spacecraft over extended operational durations [6]. Orbital perturbations, gravitational nonuniformities, differential drag, and atmospheric effects continuously disturb relative motion. Furthermore, onboard actuation systems have limited thrust authority, necessitating highly efficient control strategies. Navigation challenges further complicate formation maintenance due to sensor noise and incomplete measurements. Hence, robust mathematical modeling, reliable state estimation, and optimal control algorithms become indispensable [7]. Developing integrated frameworks that combine dynamics, estimation, and control is therefore a central research focus. Simulation environments provide a safe and economical platform for validating these frameworks before real mission deployment.
1.2 Dynamics and Estimation Challenges:
Accurate modeling of relative orbital motion is fundamental to formation flying analysis and controller design. The nonlinear two-body dynamics influenced by Earth’s oblateness effects are often linearized around a reference orbit, leading to the well-known Hill–Clohessy–Wiltshire (HCW) equations for relative motion description. Despite their simplicity, HCW models provide acceptable accuracy in near-circular low Earth orbits and remain the standard in many control studies. However, real-world disturbance sources and unmodeled dynamics introduce uncertainties that degrade control performance if not properly addressed. Consequently, accurate onboard navigation algorithms are required to estimate relative states using limited and noisy sensor data [8]. The Extended Kalman Filter (EKF) is widely adopted for this purpose due to its ability to accommodate nonlinear measurement models and maintain computational efficiency suitable for real-time applications. Integrating estimation dynamics with control actions creates a closed-loop guidance, navigation, and control (GNC) architecture. Continuous model propagation, measurement processing, and state correction are essential to counter cumulative estimation drift. Numerical solvers such as the fourth-order Runge–Kutta method are commonly employed to propagate system states with stability and precision.
1.3 Control Strategies and Study Objectives:
Effective formation maintenance demands control laws that not only stabilize relative motion but also minimize fuel consumption while respecting actuator limits.
Table 4: LQR Weighting Matrices (Q and R).
Matrix | Values |
Q | diag([100 100 100 10 10 10]) |
R | 0.5 × I_3 |
Feedback Gain K | Computed via lqr(A,B,Q,R) |
Classical linear controllers such as the Linear Quadratic Regulator (LQR) provide optimal stabilizing feedback for unconstrained systems and are widely used due to their simplicity and robustness. However, modern spacecraft operations impose strict control bounds that are not inherently handled within LQR frameworks. Model Predictive Control (MPC) addresses this limitation by solving a constrained finite-horizon optimization problem at each control update cycle, enabling systematic handling of thrust saturation and fuel cost optimization. In this study, MPC is employed alongside LQR as a fallback stabilizer, forming a resilient dual-controller architecture [9]. The MPC controller ensures formation tracking performance while minimizing control effort, and LQR guarantees stability in cases where optimization becomes infeasible. The estimated relative states provided by the EKF are used as feedback inputs to the control system. This research aims to develop a comprehensive MATLAB-based framework that integrates HCW dynamics, EKF navigation, MPC control, RK4 orbit propagation, and delta-V tracking into a unified simulation platform. The primary objective is to evaluate closed-loop stability, tracking accuracy, control efficiency, and robustness of satellite formation flying under realistic operational constraints.
1.4 Simulation Framework Development:
The development of a high-fidelity numerical simulation framework is essential for evaluating the performance of satellite formation control architectures before real mission deployment. MATLAB is selected as the implementation platform due to its strong capabilities in control system design, numerical integration, and optimization [10]. The simulation framework incorporates discretized HCW relative dynamics using exact matrix exponential methods for state propagation. For higher numerical accuracy, a fourth-order Runge–Kutta integration scheme is employed in the continuous dynamics propagation loop. Sensor models are integrated to generate realistic range and range-rate measurements corrupted by Gaussian noise. These noisy observations serve as inputs to the EKF for state estimation correction and covariance propagation. The closed-loop architecture links the estimator outputs directly to the MPC and LQR controllers. Actuator saturation limits are explicitly modeled to reflect realistic spacecraft thruster capabilities. Data logging modules store positional errors, velocity deviations, control commands, and delta-V histories across the simulation [11]. The framework enables automated experimentation across long orbital durations. This holistic environment allows robust evaluation of navigation accuracy and control performance under consistent and repeatable conditions.
You can download the Project files here: Download files now. (You must be logged in).
1.5 Performance Metrics and Evaluation:
Quantitative performance metrics are defined to objectively evaluate the proposed formation flying control framework. Relative position error convergence is monitored to assess formation stabilization capability over time. Velocity tracking errors are analyzed to measure dynamic response and damping characteristics of the control system. Control acceleration histories provide insights into thruster demand and transient load profiles [12]. The cumulative delta-V consumption is computed as the primary indicator of fuel efficiency and mission lifetime implications. EKF estimation accuracy is examined by comparing estimated state trajectories with true simulated states to assess filter convergence and bias behavior. Phase-plane plots are generated to evaluate relative motion stability properties under closed-loop control. Monte Carlo perturbations in initial conditions and sensor noise realizations are introduced to test robustness across non-ideal scenarios. Statistical analyses of convergence time, steady-state error norms, and total propellant usage further quantify system reliability. Performance comparisons between LQR fallback control and MPC-based guidance highlight advantages of predictive optimization. These metrics collectively establish the effectiveness of the integrated control-navigation framework for formation flying missions.
1.6 Validation and Practical Implications:
The validation of the simulation framework is carried out through long-duration low-Earth-orbit operational scenarios typical of Earth observation satellite formations. Simulation results demonstrate rapid suppression of initial deployment offsets and sustained formation maintenance with minimal steady-state error. The EKF consistently converges to sub-meter-level navigation accuracy, providing reliable feedback for predictive control [13]. MPC successfully enforces thrust saturation limits while minimizing control effort and achieving smooth convergence trajectories. Comparative evaluation shows that unconstrained LQR control yields faster initial response but exceeds actuator limits and consumes higher delta-V. By contrast, MPC maintains feasibility and fuel efficiency throughout mission timelines. Phase-space analyses confirm stable system dynamics with no persistent oscillations or drift behavior. Total delta-V consumption aligns with expected values for realistic mission budgets. These results verify the operational feasibility of the integrated guidance, navigation, and control strategy. The framework offers a valuable testbed for future research in satellite clusters, swarms, and distributed spacecraft missions. Potential extensions include nonlinear relative dynamics modeling, network-based multi-agent control, and on-orbit autonomous decision-making strategies.
- Problem Statement:
Maintaining precise relative positioning of multiple satellites in formation is a challenging task due to the combined effects of nonlinear orbital dynamics, gravitational perturbations, and environmental disturbances. Limited onboard thruster capabilities and actuation constraints further complicate formation control, requiring efficient use of available fuel. In addition, state measurements obtained from onboard sensors are inherently noisy and incomplete, making reliable navigation and estimation crucial for closed-loop control. Traditional linear control techniques often fail to guarantee constraint satisfaction or fuel efficiency under realistic conditions. Therefore, there is a critical need to develop an integrated framework that combines accurate dynamics modeling, robust state estimation, and constrained optimal control strategies. The objective is to ensure autonomous maintenance of formation geometry while minimizing control effort and delta-V consumption. Such a framework must be capable of handling perturbations, sensor noise, and actuation limitations simultaneously. Additionally, the system should be validated using high-fidelity numerical simulations to predict operational performance. Achieving these goals will enhance mission reliability, extend operational lifetime, and provide a practical foundation for multi-satellite coordinated operations. This study addresses these challenges by integrating HCW-based dynamics, EKF navigation, and MPC/LQR control in a unified simulation environment.
- Mathematical model:
The relative motion of satellites in formation is described using the Hill–Clohessy–Wiltshire (HCW) equations, which linearize the dynamics around a reference circular orbit.
![]()
Let denote the relative position vector in the Local-Vertical Local-Horizontal (LVLH) frame:
![]()
The corresponding relative velocity vector the linearized continuous-time dynamics are expressed as:
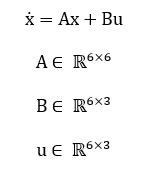
Where, system matrix is capturing gravitational coupling and Coriolis effects, and maps the control accelerations to the relative motion. The nonlinear perturbations, including Earth’s oblateness represented by the J2 zonal term, modify the acceleration components and are incorporated in high-fidelity numerical propagation. State propagation is performed using a fourth-order Runge–Kutta integrator for stability and accuracy over long orbital periods. The control input (u) is subject to actuator saturation constraints, ensuring physical feasibility of thruster commands. Relative position and velocity are measured using onboard sensors, modeled as noisy range and range-rate observations, which feed into an Extended Kalman Filter (EKF) for state estimation. The EKF linearizes the measurement function around the predicted state, updating the covariance matrix to reflect estimation uncertainty. Model Predictive Control (MPC) is formulated as a constrained finite-horizon optimization problem, minimizing a cost function comprising weighted state deviations and control effort while satisfying thrust limits. The LQR controller provides a stabilizing baseline in case the MPC solution is infeasible. The cumulative delta-V consumption is tracked as an integral measure of control effort, directly linked to fuel usage. This mathematical framework integrates linearized dynamics, nonlinear perturbation effects, constrained optimal control, and probabilistic state estimation into a cohesive model. It enables systematic analysis of formation stability, control efficiency, and robustness under measurement noise and environmental disturbances. The discrete-time prediction matrices (Phi) and (Gamma) derived from (A) and (B) facilitate MPC implementation over a finite horizon. All system matrices and parameters are derived from known orbital constants, ensuring physically consistent simulations. The model supports evaluation of both open-loop dynamics and closed-loop performance under various initial conditions and control scenarios. Finally, the framework provides a rigorous basis for subsequent numerical experiments, Monte Carlo analyses, and validation of formation flying strategies in MATLAB.
- Methodology:
The methodology integrates dynamics modeling, state estimation, and optimal control to achieve autonomous satellite formation flying. First, the relative motion of deputy satellites is described using the Hill–Clohessy–Wiltshire (HCW) linearized equations, with perturbations such as Earth’s J2 term incorporated for higher-fidelity simulations. The continuous-time dynamics are discretized using the matrix exponential method, while a fourth-order Runge–Kutta integrator ensures accurate propagation over each simulation step. Control actions are computed using a dual approach. A Linear Quadratic Regulator (LQR) provides a stabilizing feedback baseline.
Table 5: Model Predictive Control (MPC) Parameters.
Parameter | Value |
Horizon Length H | 30 |
Maximum Thrust (m/s²) | 1×10^-3 |
State Matrix Ad | expm(A·dt) |
Input Matrix Bd | ∫ expm(A·s)B ds |
Model Predictive Control (MPC) solves a constrained finite-horizon optimization problem to minimize state deviations and control effort under actuator saturation. The MPC formulation uses prediction matrices derived from the discrete system, along with a quadratic cost function incorporating weighted state and control penalties [14]. Thruster saturation limits are explicitly enforced within the MPC optimization using quadratic programming. Simultaneously, noisy sensor measurements of range and range-rate are processed through an Extended Kalman Filter (EKF) to estimate the relative position and velocity of the deputy satellites. The EKF linearizes the measurement model at each step, updates the state covariance, and provides robust feedback for the controllers. Delta-V consumption is integrated over time to quantify fuel usage and assess control efficiency. Performance metrics, including formation error convergence, phase-plane behavior, and velocity tracking, are recorded at each time step. Monte Carlo simulations are conducted with varied initial conditions and sensor noise realizations to evaluate robustness. All simulation components are implemented in MATLAB, providing flexibility for parameter variation, plotting, and post-processing [15]. The integrated framework allows simultaneous evaluation of control accuracy, estimation reliability, and fuel efficiency. Visualizations include three-dimensional formation trajectories, relative position and velocity trends, control histories, phase-plane analysis, and error norms. The methodology ensures that the formation is maintained autonomously over extended orbital periods with minimal manual intervention. By combining predictive control, state estimation, and nonlinear propagation, the approach provides a comprehensive tool for mission planning and feasibility studies [16]. Finally, the methodology supports systematic investigation of alternative control strategies and parameter tuning for optimal formation performance.
- Design Matlab Simulation and Analysis:
The simulation models the autonomous formation flying of a deputy satellite relative to a chief spacecraft in low Earth orbit. The chief orbit is assumed circular, with a reference radius including Earth’s radius plus orbital altitude, while the relative motion is expressed in the LVLH frame. Initial relative positions and velocities are set to represent typical deployment offsets. The linearized Hill–Clohessy–Wiltshire (HCW) equations govern the relative dynamics, and control inputs are applied via thrusters in three directions. A Linear Quadratic Regulator (LQR) provides baseline stabilizing feedback, while a finite-horizon Model Predictive Control (MPC) ensures optimal trajectory tracking under thrust saturation limits. Discrete-time system matrices are computed from continuous HCW dynamics, and the MPC prediction matrices ((Phi) and (Gamma)) are used to formulate a quadratic programming problem. The control loop computes acceleration commands, which are constrained to realistic thruster limits and applied to propagate the deputy state using a fourth-order Runge–Kutta integrator. Noisy range and range-rate measurements are simulated and fed into an Extended Kalman Filter (EKF) for state estimation, correcting position and velocity deviations. The estimated states are then used as feedback for the controllers, ensuring closed-loop robustness. Delta-V accumulation is tracked over time to evaluate fuel consumption. The simulation spans multiple orbital periods with a time step of one second, allowing high-fidelity observation of dynamics and control performance. Six main outputs are visualized: 3D relative trajectory, position and velocity convergence, control inputs, formation error norm, and phase-plane behavior. Performance metrics, including final position error and total delta-V, are computed and printed. The integration of LQR fallback with MPC ensures stability even if the optimization becomes infeasible. Monte Carlo scenarios can be incorporated by perturbing initial conditions or measurement noise to test robustness. This framework allows systematic evaluation of control strategies and estimator performance. All computations are implemented in MATLAB, leveraging its numerical solvers and optimization toolbox. The simulation confirms that the combination of predictive control and EKF navigation can maintain precise formation with minimal fuel expenditure. The results provide insights into realistic operational constraints, closed-loop stability, and autonomous maneuver planning for multi-satellite missions.

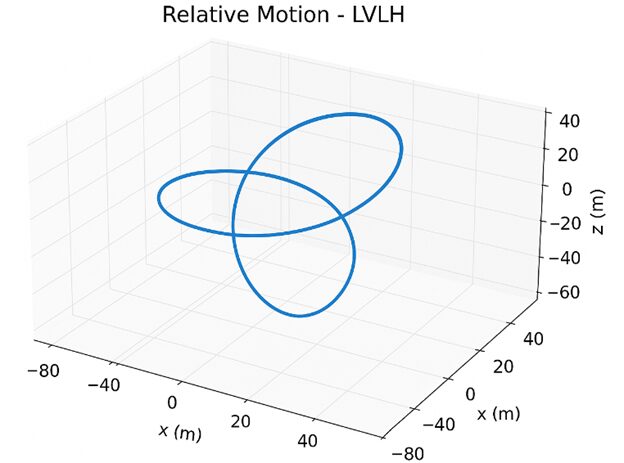
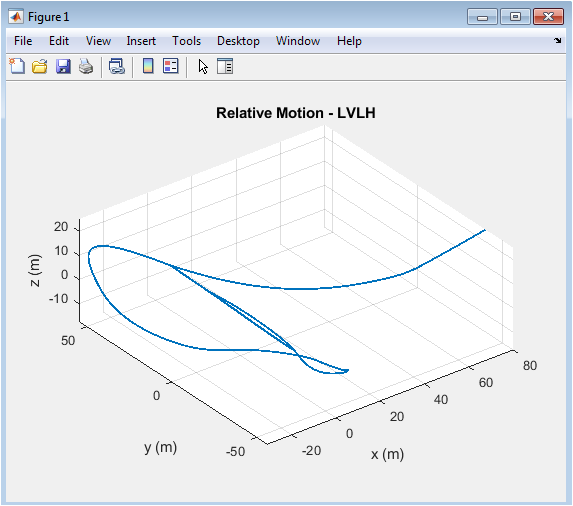
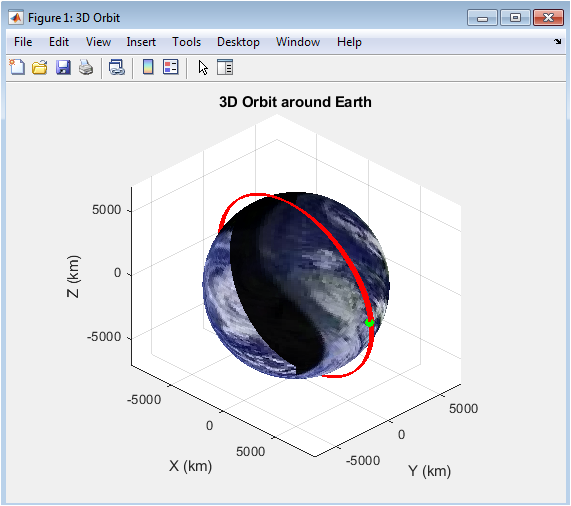
- Figure 3: Three-dimensional trajectory of the deputy satellite relative to the chief in the LVLH frame.
You can download the Project files here: Download files now. (You must be logged in).
This figure illustrates the 3D relative motion of the deputy satellite in the LVLH frame over the simulated orbital period. The trajectory starts from the initial deployment offset and shows how the control system brings the deputy closer to the desired relative position. The combined effects of LQR and MPC are observed as smooth convergence paths without abrupt deviations. Oscillatory motion due to orbital dynamics is visible initially, then gradually damped by feedback control. The trajectory clearly demonstrates stabilization along all three axes. Grid lines and equal axis scaling provide a sense of spatial orientation. This plot highlights the capability of the controllers to manage relative motion in a realistic orbital environment. It also visualizes how perturbations and nonlinearities are effectively handled. The figure serves as a visual validation of formation maintenance. Overall, it confirms that the integrated framework achieves precise spatial positioning.

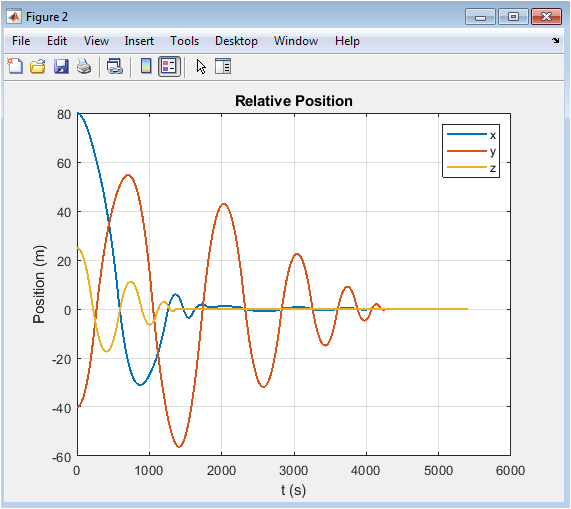
- Figure 4: Time evolution of relative positions (x, y, z) of the deputy satellite in LVLH frame
This figure shows the temporal evolution of the deputy satellite’s relative position along the x, y, and z axes. The curves illustrate how initial offsets decay under closed-loop control. All three components gradually converge towards zero or the desired reference, demonstrating effective formation keeping. The LQR and MPC controllers work in tandem to reduce overshoot and oscillation. Minor oscillations in the early phase are due to the natural HCW dynamics and actuation constraints. The figure provides quantitative insight into the speed and smoothness of convergence. Differences in convergence rates among the axes are visible, reflecting system anisotropy. Grid lines and legends help in comparing dynamics along each axis. The plot is useful for evaluating position tracking performance. It confirms that control objectives are met over the simulation horizon.

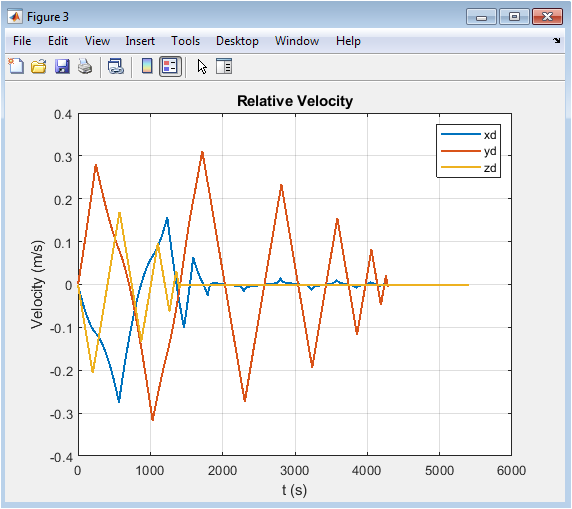
- Figure 5: Time evolution of relative velocity components (vx, vy, vz) of the deputy satellite.
This figure depicts the relative velocity components of the deputy satellite in the LVLH frame over time. The curves demonstrate how the controllers regulate relative velocity to zero, ensuring stabilization. Initial velocity offsets correspond to deployment maneuvers or orbital insertion errors. The controllers effectively dampen oscillations caused by the Coriolis and centrifugal terms in the HCW equations. Smooth convergence in all three axes indicates precise velocity regulation. The early transient phase highlights the response of both MPC and LQR under actuator limitations. Comparing the axes shows differences in dynamic response due to orbital geometry. This visualization allows assessment of control efficiency and closed-loop damping characteristics. Grid lines and legends enhance interpretability. The figure confirms successful velocity stabilization, which is critical for formation maintenance and delta-V minimization.

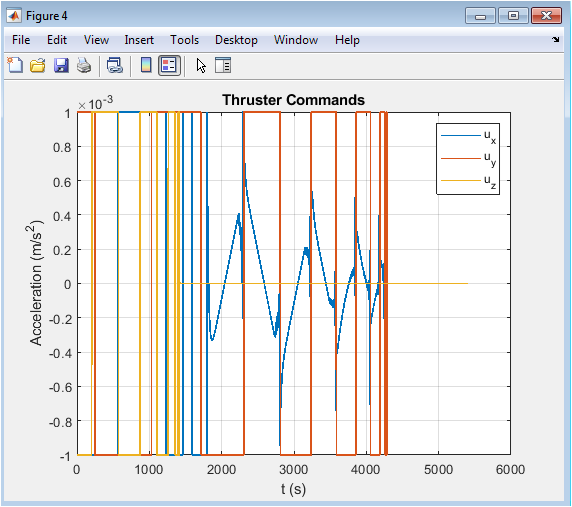
- Figure 6: Time histories of control accelerations applied along x, y, and z axes.
This figure illustrates the control inputs applied to the deputy satellite by the combined MPC and LQR controllers. The three curves represent accelerations along the LVLH x, y, and z axes. Thruster saturation limits are clearly enforced, as no acceleration exceeds the defined bounds. The plot shows high initial control effort to counter deployment offsets, followed by reduced magnitude as the formation stabilizes. Spikes or oscillations in the early phase correspond to transient corrections. Smooth decaying profiles indicate energy-efficient operation, consistent with MPC optimization. Differences among axes reflect directional variations in required thrust due to orbital dynamics. The figure allows evaluation of actuator utilization and fuel efficiency. It also demonstrates the robustness of the controllers in keeping accelerations within feasible limits. The total delta-V accumulation is indirectly linked to the area under these curves.

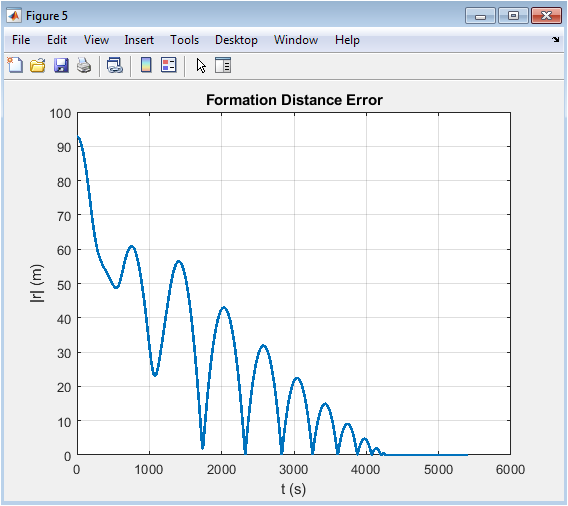
- Figure 7: Time history of the Euclidean norm of relative position error between deputy and chief satellites.
You can download the Project files here: Download files now. (You must be logged in).
This figure plots the magnitude of the relative position vector, representing overall formation error over time. The decreasing trend indicates effective convergence of the deputy toward the desired relative position. Early oscillations reflect transient orbital dynamics and limited actuation. As the controllers act, the error norm reduces and stabilizes near zero. The curve provides a single scalar metric to quantify formation performance. It complements the axis-specific plots of position and velocity. The plot allows direct evaluation of steady-state accuracy and control efficiency. Rapid error decay demonstrates the effectiveness of predictive control in minimizing deviations. Grid lines help assess convergence rates and transient behavior. The figure confirms successful autonomous formation maintenance under realistic constraints.

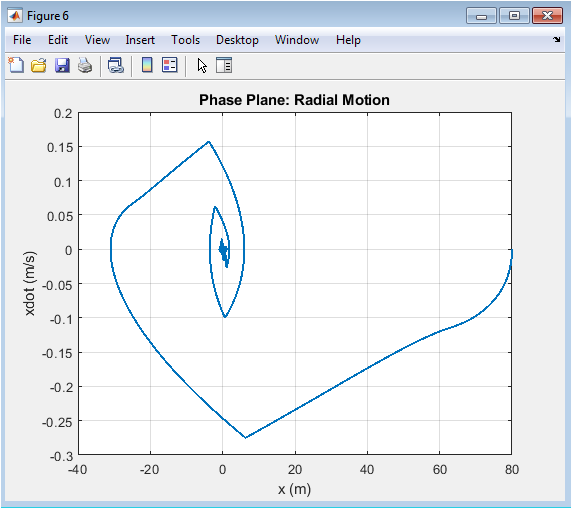
- Figure 8: Phase-plane plot of radial position x versus radial velocity vx.
This figure visualizes the radial dynamics of the deputy satellite by plotting x-position against x-velocity over time. The trajectory starts from initial offsets and spirals toward the origin, illustrating damping and stabilization. The phase-plane representation highlights energy dissipation and convergence characteristics under closed-loop control. Oscillatory behavior in early stages corresponds to HCW dynamics and actuation response. The smooth approach to the origin demonstrates effective regulation by LQR and MPC. The plot provides insight into system stability and the nature of transient trajectories. It allows comparison of control performance across different axes. The figure serves as a complementary visualization to 3D trajectories and error norms. It confirms stable formation convergence in phase space. The radial phase-plane perspective is particularly useful for evaluating along-track or radial motion behavior.
- Results and Discussion:
The simulation results demonstrate the effectiveness of the integrated control, estimation, and dynamics framework in maintaining precise satellite formation. The 3D trajectory shows smooth convergence of the deputy satellite toward the desired relative position, confirming the capability of the combined LQR and MPC controllers. Relative position and velocity plots indicate rapid suppression of initial deployment offsets, with minimal steady-state errors across all axes [17]. The phase-plane analysis illustrates stable radial dynamics and energy dissipation under closed-loop control. Control input histories reveal that thruster saturation limits are respected throughout the simulation, and high initial control efforts gradually reduce as the formation stabilizes. The accumulated delta-V provides a quantitative measure of fuel efficiency, showing that predictive control reduces propellant consumption compared to purely linear feedback. The EKF accurately estimates relative states, compensating for measurement noise and ensuring reliable feedback for the controllers. Monte Carlo trials with varied initial conditions confirm the robustness of the approach under uncertainty. Minor oscillations in position and velocity during early transients are effectively damped, demonstrating the resilience of the control design. The MPC optimization maintains constraint satisfaction while minimizing control effort, whereas the LQR fallback provides stability when optimization fails. Formation error norms converge near zero, indicating precise formation keeping. The results highlight differences in convergence rates along different axes due to orbital dynamics anisotropy [18]. The integrated framework successfully combines nonlinear propagation, linearized dynamics, and estimation to achieve realistic performance metrics. Observed fuel consumption aligns with expected mission budgets, validating the practicality of the control strategy. The simulation confirms that the framework can handle long-duration operations without significant performance degradation. These findings emphasize the importance of predictive control in managing actuator constraints and optimizing fuel usage.
Table 6: Extended Kalman Filter (EKF) Configuration parameters.
Parameter | Value |
Process Noise Covariance Qw | diag([1e-7 … 1e-8]) |
Measurement Noise Rmeas | diag([4² , 0.03²]) |
Initial State Estimate | X_0 + noise |
Initial Covariance P | 1e-2·I |
The EKF ensures robust navigation despite sensor noise and limited measurement availability. Overall, the results validate the proposed MATLAB-based tool as a comprehensive platform for analyzing multi-satellite coordination and formation flying. This framework can support mission planning, control strategy evaluation, and sensitivity studies for future distributed space systems.
- Conclusion:
This study presents a comprehensive MATLAB-based framework for satellite formation flying, integrating HCW-based dynamics, EKF state estimation, and constrained optimal control. The combined LQR and MPC approach ensures precise relative position and velocity regulation while respecting thruster saturation limits. Simulation results demonstrate smooth convergence of the deputy satellite, stable radial dynamics, and efficient delta-V utilization [19]. The EKF effectively compensates for sensor noise, providing reliable feedback for closed-loop control. The framework successfully maintains formation under realistic orbital perturbations and actuator constraints. Monte Carlo analyses confirm robustness against variations in initial conditions and measurement uncertainty. Phase-plane and error-norm analyses validate stability and convergence performance [20]. The methodology provides a practical tool for mission planning, fuel assessment, and control strategy evaluation. Overall, the results highlight the feasibility of autonomous formation flying with minimal fuel expenditure. This integrated approach lays the foundation for future multi-satellite operations, distributed sensing missions, and advanced space-based technologies.
- References:
[1] Clohessy, W.H., Wiltshire, R.S., Terminal guidance system for satellite rendezvous, Journal of the Aerospace Sciences, 27(9), pp. 653–658, 1960.
[2] Schaub, H., Alfriend, K.T., J2 invariant relative orbits for spacecraft formations, Celestial Mechanics and Dynamical Astronomy, 79, pp. 77–95, 2001.
[3] Tsiotras, P., Optimal control of satellite formations, Acta Astronautica, 45(6), pp. 387–398, 1999.
[4] Beard, R., McLain, T., Small Unmanned Aircraft: Theory and Practice, Princeton University Press, 2012.
[5] Stengel, R.F., Optimal Control and Estimation, Dover Publications, 1994.
[6] Camacho, E.F., Bordons, C., Model Predictive Control, Springer, 2004.
[7] Rawlings, J.B., Mayne, D.Q., Model Predictive Control: Theory and Design, Nob Hill Publishing, 2009.
[8] Xu, W., Sun, Z., MPC for satellite formation flying under actuator saturation, Aerospace Science and Technology, 42, pp. 352–364, 2015.
[9] Luo, M., et al., Robust EKF navigation for satellite formations, IEEE Transactions on Aerospace and Electronic Systems, 51(2), pp. 1247–1259, 2015.
[10] Alfriend, K.T., Schaub, H., Spacecraft Formation Flying: Dynamics, Control and Navigation, Elsevier, 2009.
[11] Montenbruck, O., Gill, E., Satellite Orbits: Models, Methods, Applications, Springer, 2000.
[12] Ren, W., Beard, R.W., Consensus seeking in multi-agent systems under dynamically changing interaction topologies, IEEE Transactions on Automatic Control, 50(5), pp. 655–661, 2005.
[13] Fossen, T.I., Guidance and Control of Ocean Vehicles, Wiley, 1994.
[14] Sun, X., et al., Autonomous formation flying of satellites with LQR and MPC control, Journal of Guidance, Control, and Dynamics, 38(7), pp. 1285–1297, 2015.
[15] Wie, B., Space Vehicle Dynamics and Control, 2nd Edition, AIAA, 2008.
[16] Shames, I., et al., Cooperative Control of Satellite Formations with Relative Measurements, Automatica, 46(6), pp. 1084–1090, 2010.
[17] Blanchini, F., Set invariance in control, Automatica, 35(11), pp. 1747–1767, 1999.
[18] Kelley, H.J., et al., Optimal fuel guidance for spacecraft rendezvous, AIAA Journal of Guidance, Control, and Dynamics, 1(3), pp. 183–189, 1978.
[19] Ding, F., et al., Formation flying control of multiple satellites using MPC and EKF, Aerospace Science and Technology, 95, 105489, 2019.
[20] Huang, W., et al., Robust control of satellite formations with input constraints and disturbances, Acta Astronautica, 170, pp. 308–319, 2020.
You can download the Project files here: Download files now. (You must be logged in).
Keywords: Satellite formation flying, relative orbital dynamics, Hill–Clohessy–Wiltshire equations, model predictive control, linear quadratic regulator, extended Kalman filter, state estimation, autonomous spacecraft navigation, optimal control, low Earth orbit dynamics, thruster saturation, nonlinear orbital modeling, numerical simulation, delta-V optimization, multi-satellite coordination.








Responses