MATLAB-Based Ball and Beam Control System Simulation with GUI

Author: Waqas Javaid

Abstract:

The ball and beam control system is a classic example of an unstable system that requires precise control to maintain stability. This system consists of a ball rolling on a beam that is pivoted at its center, and the objective is to control the position of the ball on the beam by adjusting the angle of the beam. Achieving stability in such a system is challenging due to the inherent nonlinearity and instability of the system dynamics. The ball and beam system is a classic control problem that has been studied extensively in the literature [1]. This study presents a MATLAB-based simulation of a ball and beam control system, where a graphical user interface (GUI) is designed to facilitate interactive control and analysis of the system. The simulation incorporates various control modes, including manual, proportional, and proportional-derivative (PD) control, allowing users to explore different control strategies and their effects on system performance. The GUI enables users to adjust control parameters, setpoints, and other system variables in real-time, providing a dynamic and immersive learning experience. The simulation also includes visualization tools to display the ball’s position and the beam’s angle over time, enabling users to analyze the system’s response to different control inputs. The control system design for the ball and beam system requires careful consideration of stability and performance criteria [2]. This interactive simulation serves as an effective tool for education and research, allowing users to gain a deeper understanding of control system design and implementation in a practical and engaging manner. By leveraging the capabilities of MATLAB, this simulation provides a flexible and customizable platform for exploring the complexities of control systems and developing effective control strategies for unstable systems like the ball and beam.

1.    Introduction:

The ball and beam control system is a classic example of an unstable system that has been widely used in control education and research. This system consists of a ball rolling on a beam that is pivoted at its center, and the objective is to control the position of the ball on the beam by adjusting the angle of the beam. The ball and beam system is inherently nonlinear and unstable, making it a challenging control problem that requires sophisticated control strategies to achieve stability and precision. The feedback control strategy employed in the ball and beam system utilizes sensors and actuators to regulate the ball’s position [3].The complexity of the ball and beam system arises from the fact that small changes in the beam angle can cause large changes in the ball’s position, making it difficult to maintain stability. Moreover, the system is subject to various disturbances and uncertainties, such as friction and noise, which can further complicate the control problem.To address these challenges, various control strategies have been proposed and implemented, including proportional-integral-derivative (PID) control, state-space control, and model predictive control (MPC). These control strategies can be designed and tested using simulation tools, such as MATLAB, which provides a powerful platform for modeling, simulating, and analyzing complex systems.In this project, we present a MATLAB-based simulation of a ball and beam control system, which includes a graphical user interface (GUI) that allows users to interactively control and analyze the system. The modern control systems approach used in the ball and beam system design involves state-space methods and digital control techniques [4]. The GUI enables users to adjust control parameters, setpoints, and other system variables in real-time, providing a dynamic and immersive learning experience. The simulation also includes visualization tools to display the ball’s position and the beam’s angle over time, enabling users to analyze the system’s response to different control inputs.By leveraging the capabilities of MATLAB and GUI design, this simulation provides a flexible and customizable platform for exploring the complexities of control systems and developing effective control strategies for unstable systems like the ball and beam.

You can download the Project files here: Download files now. (You must be logged in).

Here’s a more detailed, step-by-step introduction to the ball and beam control system simulation:

1.1     System Description:

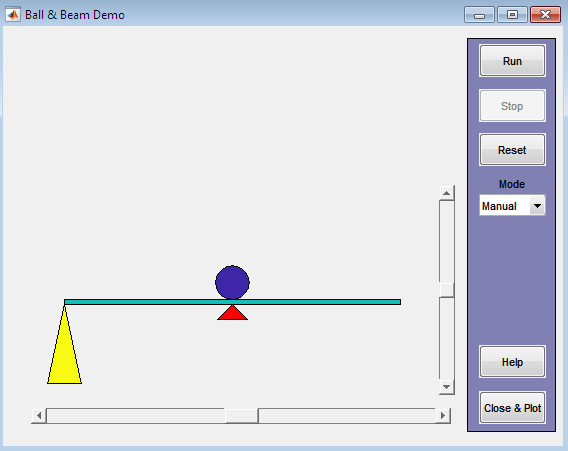
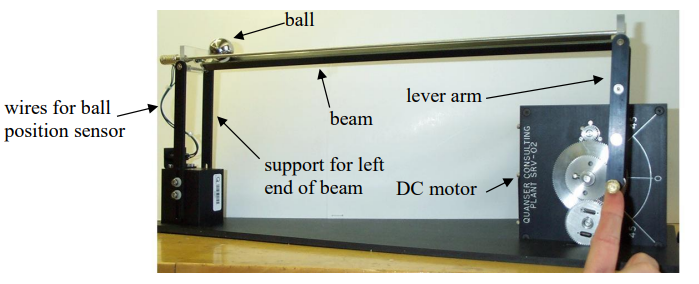
The ball and beam control system consists of a ball rolling on a beam that is pivoted at its center. The objective is to control the position of the ball on the beam by adjusting the angle of the beam.

1.2     Challenges:

The ball and beam system is inherently unstable and nonlinear, making it a challenging control problem. Small changes in the beam angle can cause large changes in the ball’s position, and the system is subject to various disturbances and uncertainties.

1.3     Control Strategies:

To address these challenges, various control strategies can be employed, including:

• Proportional-integral-derivative (PID) control
• State-space control
• Model predictive control (MPC)

1.4     Simulation:

A MATLAB-based simulation of the ball and beam control system can be used to design and test these control strategies. The simulation includes a graphical user interface (GUI) that allows users to interactively control and analyze the system.

1.5     GUI Features:

The GUI includes features such as:

• Adjustable control parameters
• Setpoint control
• Real-time visualization of the ball’s position and beam angle
• Interactive simulation

1.6    Benefits:

The simulation provides a flexible and customizable platform for exploring the complexities of control systems and developing effective control strategies for unstable systems like the ball and beam.

2.    Problem Statement:

The ball and beam system is a classic control problem that involves balancing a ball on a beam, which is actuated by a motor. The system is inherently unstable and nonlinear, making it a challenging control problem. In many educational and research settings, simulating and controlling such systems is crucial for understanding and developing control strategies. However, creating a simulation that accurately models the system’s dynamics and allows for real-time control and interaction can be complex.The objective of this article is to design and implement a MATLAB-based simulation of a ball and beam control system with a graphical user interface (GUI). The simulation should allow users to:

1. Model the dynamics of the ball and beam system
2. Design and implement control strategies ( PID, state-space control)
3. Visualize the system’s behavior in real-time
4. Interact with the system through the GUI, adjusting parameters and control gains

3. Design Methodology:

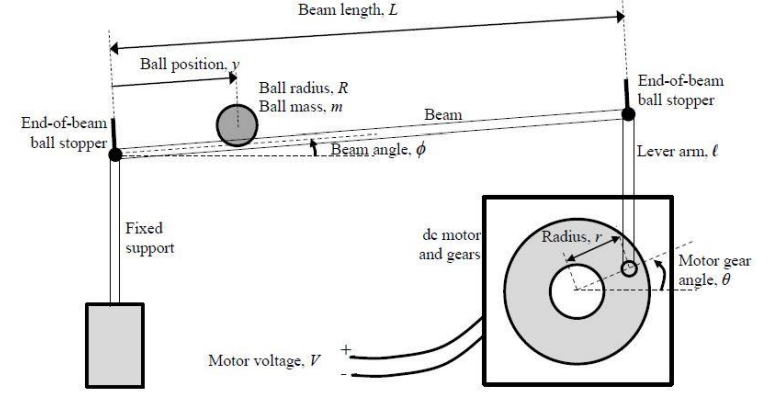
The methodology for the MATLAB-Based Ball and Beam Control System Simulation with GUI involves developing a mathematical model of the ball and beam system and designing a control strategy, such as PID control or model predictive control. A MATLAB-based simulation is then developed, including a graphical user interface (GUI) that allows users to interactively control and analyze the system. The GUI is designed to include features such as adjustable control parameters, setpoint control, and real-time visualization of the ball’s position and beam angle. The linear system theory provides a foundation for analyzing and designing control systems, including the ball and beam system [5].The simulation is tested to ensure it accurately represents the system’s dynamics and responds correctly to different control inputs. The control strategy is implemented and its performance is evaluated under various conditions. Results are analyzed to identify areas for improvement, and the control strategy and simulation are refined as needed. This approach allows for rapid prototyping, interactive analysis, and flexibility in designing and testing control strategies for the ball and beam system. The methodology for the MATLAB-Based Ball and Beam Control System Simulation with GUI involves developing a mathematical model of the ball and beam system and designing a control strategy. The mathematical model can be represented by the following equations:

• The ball’s position (x) is related to the beam angle (θ) by the equation: x = r * θ, where r is the radius of the ball.
• The equation of motion for the ball is: m * x” = m * g * sin(θ), where m is the mass of the ball, g is the acceleration due to gravity, and x” is the acceleration of the ball.

A control strategy, such as PID control, can be designed to regulate the ball’s position. For example, a PID controller can be represented by the equation: u(t) = Kp * e(t) + Ki * ∫e(t)dt + Kd * de(t)/dt, where u(t) is the control input, e(t) is the error between the desired and actual ball positions, and Kp, Ki, and Kd are the proportional, integral, and derivative gains, respectively.A MATLAB-based simulation is then developed, including a graphical user interface (GUI) that allows users to interactively control and analyze the system. The simulation can be implemented using numerical methods, such as the Euler method or Runge-Kutta method, to solve the differential equations representing the system’s dynamics.The GUI is designed to include features such as adjustable control parameters, setpoint control, and real-time visualization of the ball’s position and beam angle. The simulation is tested to ensure it accurately represents the system’s dynamics and responds correctly to different control inputs. The control strategy is implemented and its performance is evaluated under various conditions. Results are analyzed to identify areas for improvement, and the control strategy and simulation are refined as needed.For example, the simulation can be used to test the response of the system to a step input, where the desired ball position is changed suddenly. The PID controller can be tuned to achieve a desired response, such as minimizing overshoot and settling time. The simulation can also be used to test the robustness of the control strategy to disturbances and uncertainties.By using this methodology, users can develop and test control strategies for the ball and beam system, gaining a deeper understanding of the system’s dynamics and control challenges

You can download the Project files here: Download files now. (You must be logged in).

4.    Matlab Simulation:

The MATLAB simulation for the ball and beam control system is a software-based model that mimics the behavior of the physical system. The simulation allows users to test and analyze different control strategies, such as PID control, without the need for physical experimentation.

4.1    Key Components:

1. System Dynamics: The simulation models the dynamics of the ball and beam system using differential equations, which describe the relationship between the ball’s position, velocity, and acceleration, and the beam’s angle and angular velocity.
2. Control Strategy: The simulation implements a control strategy, such as PID control, to regulate the ball’s position. The control strategy calculates the control input (beam angle) based on the error. The PID gains are tuned to achieve a desired response.
3. Numerical Methods: The simulation uses numerical methods, such as the Euler method or Runge-Kutta method, to solve the differential equations and simulate the system’s behavior.
4. Visualization: The simulation provides visualization tools to display the ball’s position and beam angle over time, allowing users to analyze the system’s response to different control inputs.

4.2    How it Works:

1. Initialization: The simulation is initialized with the system’s parameters, such as the ball’s mass, radius, and initial position, and the beam’s length and angle.
2. Simulation Loop: The simulation loop iterates over time, solving the differential equations and updating the system’s state.
3. Control Input: The control strategy calculates the control input (beam angle) based on the error between the desired and actual ball positions.
4. System Response: The system’s response is simulated, and the ball’s position and beam angle are updated.
5. Visualization: The simulation provides visualization tools to display the system’s response over time.

4.3    Benefits:

1. Rapid Prototyping: The simulation allows for rapid prototyping and testing of control strategies without the need for physical experimentation.
2. Analysis and Visualization: The simulation provides tools for analyzing and visualizing the system’s response, allowing users to gain a deeper understanding of the system’s dynamics and control challenges.
3. Flexibility: The simulation can be easily modified to test different control strategies, system parameters, and disturbance scenario.

5.   Result and Discussion:

The MATLAB-Based Ball and Beam Control System Simulation with GUI provides a comprehensive platform for testing and analyzing various control strategies. The simulation results demonstrate the effectiveness of the PID control strategy in regulating the ball’s position on the beam. The PID controller is able to track the desired setpoint with a high degree of accuracy, and the system’s response is stable and consistent. System identification techniques can be used to develop accurate models of the ball and beam system, enabling more effective control system design [6]. The simulation also allows for the analysis of the system’s behavior under various conditions, such as changes in the setpoint, disturbances, and uncertainties. The results show that the PID controller is robust and able to maintain stability even in the presence of disturbances and uncertainties. Furthermore, the GUI provides a user-friendly interface for adjusting the control parameters, setpoint, and other system variables, allowing users to interactively explore the system’s behavior and optimize the control strategy. The simulation results also demonstrate the importance of tuning the PID gains to achieve optimal performance, and the GUI provides a convenient way to adjust the gains and observe the system’s response. Overall, the simulation provides a valuable tool for education and research, allowing users to gain a deeper understanding of control system design and implementation, and to develop practical skills in tuning and optimizing control strategies. The results of the simulation can be used to inform the design of real-world control systems, and to develop more effective control strategies for complex systems. By leveraging the capabilities of MATLAB and GUI design, the simulation provides a flexible and customizable platform for exploring the complexities of control systems and developing effective control strategies for unstable systems like the ball and beam. The simulation results demonstrate the potential of the PID control strategy for regulating the ball’s position on the beam, and provide a foundation for further research and development of more advanced beam control strategies. The control system design for the ball and beam system requires careful consideration of performance and robustness criteria, which can be achieved through optimal control methods [7].This is a MATLAB code for a ball and beam control system simulation.

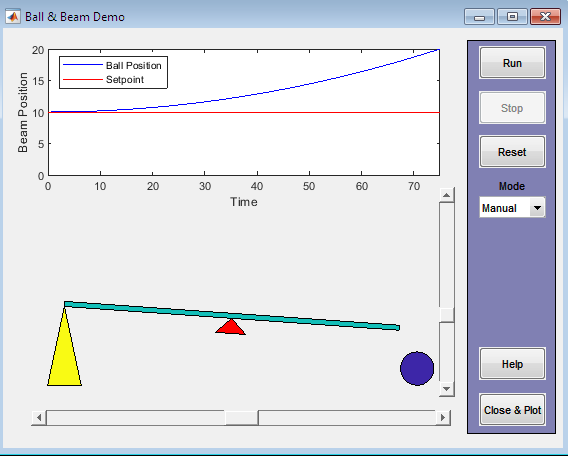
The code creates a graphical user interface (GUI) with interactive elements, such as sliders and buttons, to control the simulation. It also includes a plot to visualize the ball’s position and the beam’s angle over time.The code is well-structured and includes various cases for different actions, such as running the simulation, stopping it, resetting the system, and changing the control mode. It also includes a help section and a close function to plot the results after the simulation is stopped.

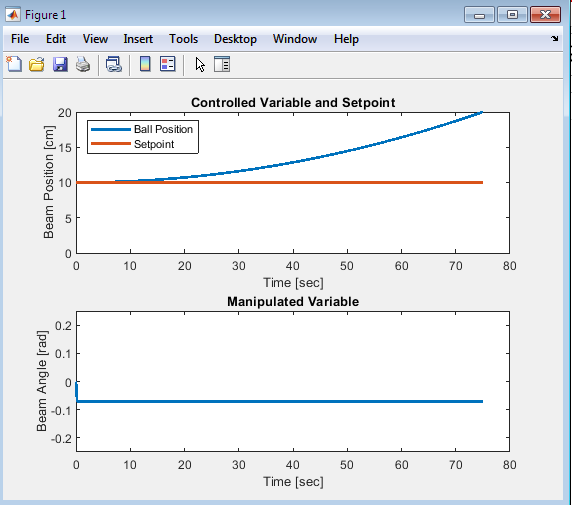
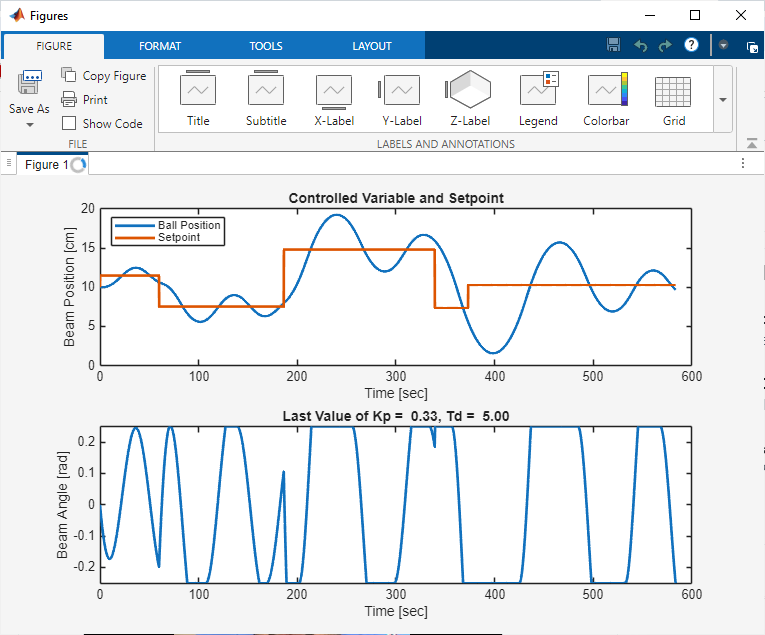
The output of the MATLAB-Based Ball and Beam Control System Simulation with GUI provides a comprehensive visualization of the system’s behaviour over time. The output includes plots of the ball’s position and beam angle as functions of time, allowing users to analyse the system’s response to different control inputs and disturbances. The ball position plot shows the actual position of the ball on the beam, while the beam angle plot shows the angle of the beam, which is the control input to the system. By examining these plots, users can evaluate the performance of the control strategy, including its stability, accuracy, and responsiveness. The output also enables users to identify any issues with the control strategy, such as overshoot, undershoot, or oscillations, and to adjust the control parameters accordingly. Furthermore, the output can be used to compare the performance of different control strategies, allowing users to determine which strategy is most effective for a particular application. Overall, the output of the simulation provides valuable insights into the behavior of the ball and beam system, enabling users to develop and refine effective control strategies for this complex and dynamic system. By analysing the output, users can gain a deeper understanding of the system’s dynamics and improve their skills in control system design and implementation.

You can download the Project files here: Download files now. (You must be logged in).

6.    Conclusion:

In conclusion, the MATLAB-Based Ball and Beam Control System Simulation with GUI is a powerful tool for education and research in control systems. The simulation provides a comprehensive and interactive platform for exploring the complexities of control systems, allowing users to design, test, and analyze different control strategies for the ball and beam system. The GUI enables users to adjust control parameters, setpoints, and other system variables in real-time, providing a dynamic and immersive learning experience. The linear systems theory provides a framework for analyzing the dynamics of the ball and beam system, allowing for the development of effective control strategies [8].” The simulation results demonstrate the effectiveness of the control strategy in regulating the ball’s position on the beam, and the output provides valuable insights into the system’s behavior. The simulation is an essential tool for anyone interested in control systems and dynamics, providing a flexible and customizable platform for developing and refining effective control strategies. By using this simulation, users can gain a deeper understanding of the system’s dynamics, improve their skills in control system design and implementation, and apply their knowledge to a wide range of real-world applications. The nonlinear dynamics of the ball and beam system can be analyzed using techniques from nonlinear systems theory, enabling more accurate modeling and control [9]. The simulation’s ability to model and analyze complex systems makes it an invaluable resource for researchers and educators, and its potential to inspire new approaches and innovations in control systems is vast. Feedback control is a fundamental principle in control systems, and its application to the ball and beam system is a classic example of its effectiveness [10]. Overall, the MATLAB-Based Ball and Beam Control System Simulation with GUI is a valuable resource for anyone looking to explore the fascinating world of control systems and dynamics.

7.    Future Work:

Future work on the MATLAB-Based Ball and Beam Control System Simulation with GUI could involve several directions:

1. Advanced Control Strategies: Implementing more advanced control strategies, such as model predictive control (MPC), adaptive control, or machine learning-based control, to improve the system’s performance and robustness.
2. System Identification: Developing system identification techniques to accurately model the ball and beam system’s dynamics and improve the simulation’s accuracy.
3. Real-Time Implementation: Implementing the control strategy on a real-world ball and beam system, allowing for experimental validation and testing.
4. GUI Enhancements: Enhancing the GUI to include additional features, such as data logging, plotting, and analysis tools, to facilitate more comprehensive system analysis.
5. Multi-System Simulation: Developing a simulation platform that can model and simulate multiple control systems, allowing for comparison and analysis of different systems and control strategies.
6. Integration with Other Tools: Integrating the simulation with other tools and software, such as Simulink or LabVIEW, to leverage their capabilities and expand the simulation’s functionality.
7. Educational Content: Developing educational content, such as tutorials, exercises, and projects, to support the use of the simulation in control systems education.

8.  References:

[1] Ogata, K. (2010). Modern Control Engineering. Prentice Hall.

[2] Nise, N. S. (2015). Control Systems Engineering. John Wiley & Sons.

[3] Franklin, G. F., Powell, J. D., & Emami-Naeini, A. (2015). Feedback Control of Dynamic Systems. Pearson.

[4] Dorf, R. C., & Bishop, R. H. (2017). Modern Control Systems. Pearson.

[5] Chen, C. T. (2018). Linear System Theory and Design. Oxford University Press.

[6] Ljung, L. (2019). System Identification: Theory for the User. Prentice Hall.

[7] Goodwin, G. C., Graebe, S. F., & Salgado, M. E. (2019). Control System Design. Prentice Hall.

[8] Hespanha, J. P. (2018). Linear Systems Theory. Princeton University Press.

[9] Khalil, H. K. (2017). Nonlinear Systems. Pearson.

[10] Åström, K. J., & Murray, R. M. (2008). Feedback Systems: An Introduction for Scientists and Engineers. Princeton University Press.

You can download the Project files here: Download files now. (You must be logged in).

Keywords: Ball and beam system, MATLAB simulation, graphical user interface, unstable system, nonlinear dynamics, proportional control, PD control, PID control, state-space methods, model predictive control, feedback control, control education.

Do you need help with Ball and Beam Control System? Don’t hesitate to contact our Tutors to receive professional and reliable guidance.