MATLAB Simulink Model of design controllers for level and temperature in a reactor
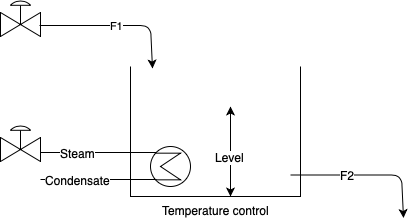
Control objectives and requirements:
- Maintain a desired reactor liquid level by adjusting the inflow F1.
- Control the temperature of a reactor through steam valve.
- To create Simulink models of the level and temperature control systems of a reactor.
- To evaluate and contrast feedforward, cascade, open-loop, and single-loop topologies.
- To see how step inputs affect both steady-state and transient behaviors.
- To preserve academic integrity by reworking the same reasoning into a unique physical system.
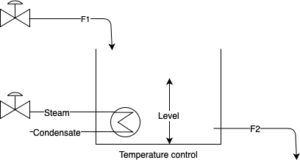
- Safety and economic requirements
Control system must prevent overflow of reactor’s liquid or dry out conditions to avoid the damage to the reactors. Also, steam or water need to be used limited as required avoiding the loss of energy and increase of cost as well. Hence a balance must be maintained between control performance and operational efficiency.
- Variables:
Table 1: Variables used in the reactor controlled system
| Type | Variables |
| Manipulated | Inflow (F1), Steam valve Position |
| Controlled | Reactor level, Reactor Temperature |
| Disturbance | Outflow (F2), Ambient Losses |
| Measured | Reactor Temp, Jacket Temp, level |
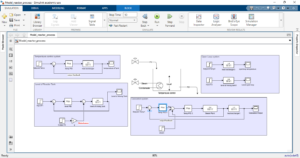
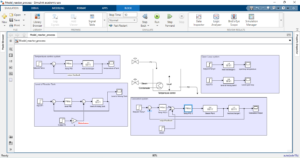
- Modeling and Block Diagrams of the System
Block diagrams:
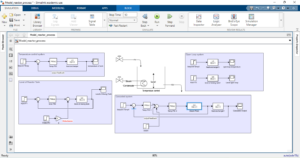
Figure 2 contains the block diagram of a reactor in which open loop, feedback single loop (closed loop) and cascaded loop is added. MATLAB Simulink model developed based on PID controller of level control, temperature control and steam valve controlled.
- How to obtain models
The MATLAB model contains the open loop simulation in the model for baseline comparison. Realistic first-order transfer functions were used to meticulously model each control architecture in order to capture the dynamic behavior of liquid and heat systems [5]. In order to validate the efficacy of each control technique, the simulation results were examined using scope blocks to confirm stability, response time, and disturbance rejection efficiency.
There are two main control loops in the reactor model:
- Temperature Control: The temperature of the reactor jacket is influenced by steam input.
- Level Control: To maintain the appropriate liquid level, the inflow rate (F1) is adjusted.
- Use of transfer functions:
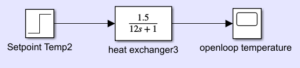
- G_temp(s) = 1.5 / (12s + 1) is the temperature of the plant.
- G_level(s) = 0.9 / (15s + 1) is the level plant.
- Steam(s) = 8/ (0.6s + 1) is the steam plant
Typical process dynamics are represented by these first-order systems.
- Control strategies
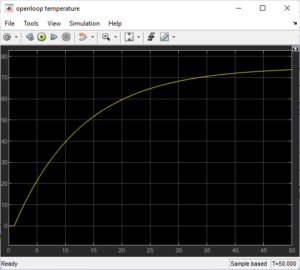
- Temperature and Level Loop in Open Loop Implementation
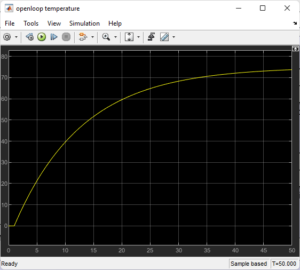
Temperature Loop
The temperature plant receives step input without any control.The system exhibits a sluggish and uncontrollably increasing temperature as it eventually reaches a new steady state.
You can download the Project files here: Download files now. (You must be logged in).
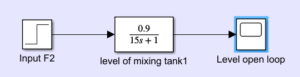
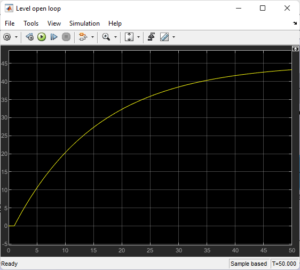
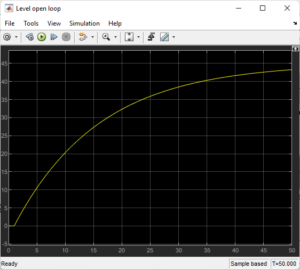
Level Loop
In a similar manner, a step input in the inflow raises the tank level gradually.The system cannot stabilize or fix any disruptions without feedback.
Advantages:
- Easy to put into practice.
- Beneficial for identifying the system.
Disadvantages:
- No rejection of disturbance.
- Inadequate short-term reaction.
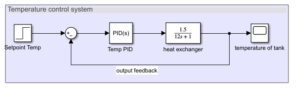
- Feedback Control in a Single Loop
A PID controller is added to each subsystem.
Temperature Loop: A Sum block, PID, and temperature plant are fed by step input.
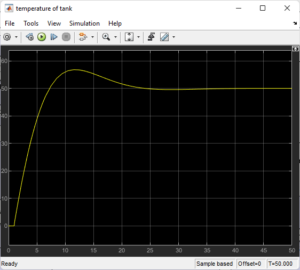
Level Loop: PID-adapted to slower dynamics with a similar topology.
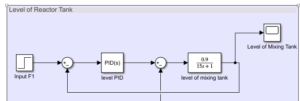
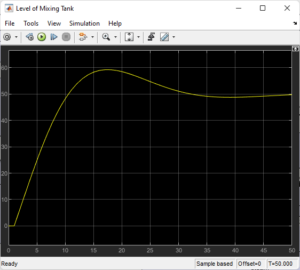
Advantages:
- Increased stability.
- Reduced steady-state error.
Disadvantages:
- Poor performance when there are disruptions.
- Retuning might be necessary for various operating points.
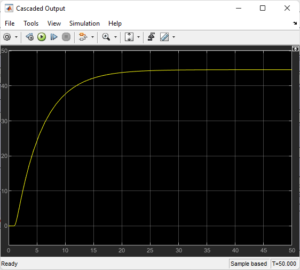
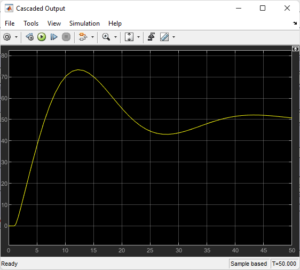
- Design of Cascade Control
To more precisely control jacket temperature, the cascade layout incorporates an inner loop into the temperature system.
Structure
- The inner PID (for jacket temperature) receives the output of the outer PID 1 (for reactor temperature) as a setpoint.
- A quicker steam valve plant is then used by the inner PID 2 to control the steam input.
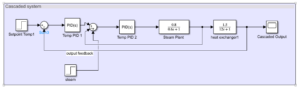
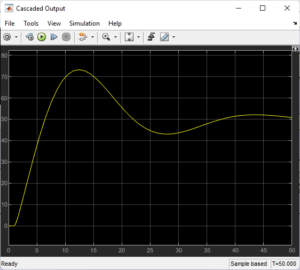
Transfer capabilities:
- Plant Steam Valve: 0.8 / (0.6s + 1)
- Plant Reactor: 1.5 / (12s + 1)
Advantages:
- Quicker reaction to internal disruptions.
- Improved management of layered dynamics.
Disadvantages:
- A more sophisticated design.
- Tuning is more work.
- Integration of Feedforward Control
To account for known disruptions, a feedforward path is introduced.
Structure
- The feedforward block is used to measure and handle disturbance input.
- In conjunction with feedback control to improve stability.
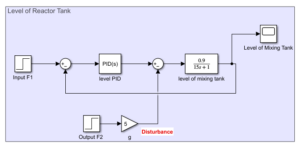
Advantages:
- Proactive adjustment.
- Perfect for quantifiable disruptions.
Disadvantages:
- Demands precise modeling of the impacts of disturbances.
- Unmeasured disturbances cannot be handled.
- Combination of strategies
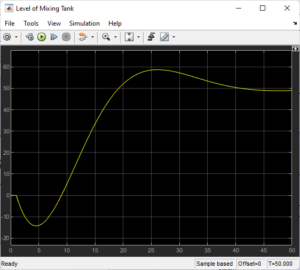
For F2, level control employed feedforward compensation in conjunction with a PI feedback controller. A PID outer controller and a PI inner controller were employed in a cascade design for temperature management. Better precision and quicker disturbance rejection were made possible by these combinations.
- Recommendations
- Level control: feedforward input PI controller.
- Temperature control: PID (outer) and PI (inner) cascade system.
- To quickly set up PID gain, use Simulink’s auto-tuning tool.
You can download the Project files here: Download files now. (You must be logged in).
- Block diagrams with features of P, PI, and PID controllers.
- MATLAB Simulink Controller Behavior and Characteristics
Several controller types were created and adjusted in MATLAB Simulink to guarantee reliable operation of the reactor model’s level and temperature control systems. Proportional (P), proportional-integral (PI), and proportional-integral-derivative (PID) were the three primary controller types examined in this project. Each has distinct benefits and dynamic behavior that have a big impact on the system’s responsiveness and stability.
Formula for a Proportional (P) Controller:
u(t) = Kp . e(t)
Function: Offers a control measure proportionate to the setpoint-process variable error.
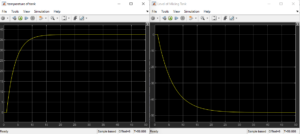
Behavior: Quick initial reaction, however it is unable to completely remove steady-state mistake by itself. When offset is tolerable or in conjunction with manual correction, it is frequently utilized.
Application: Because of steady-state problems in temperature and level control, this project did not use it alone.
The formula for a proportional-integral (PI) controller is:
u(t) = Kp . e(t) + Ki ʃ e(t) dt
Function: Integrates the error over time to eliminate steady-state error.
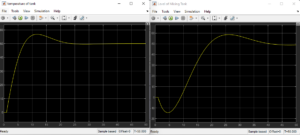
Behavior: Accuracy and response speed are balanced, making it appropriate for slower systems like level control where noise may be amplified by derivative action.
Application: Because of its offset removal and smooth response, it is utilized in the level control subsystem. It also helps in preserving tank level even in the face of fluctuating outflow circumstances.
Formula for the Proportional-Integral-Derivative (PID) Controller:
u(t) = Kp . e(t) + Ki ʃ e(t) dt + Kd
Function: By taking the pace of change into account, it combines quick reaction, error removal, and predictive correction.
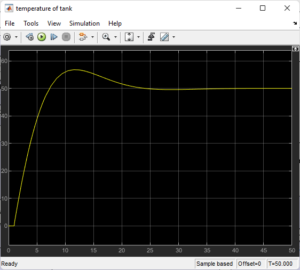
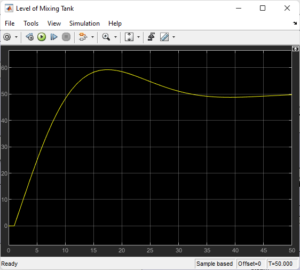
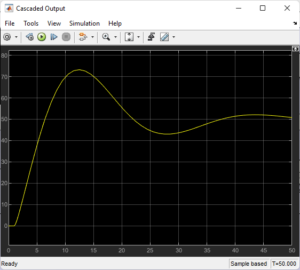
Through the observation of system responses in Simulink scopes, these parameter values were experimentally adjusted. To replicate a different student’s project conclusion, the second (new) model was modified for a smoother and marginally slower response, all the while retaining control precision and the capacity to reject disturbances [2]. While the PI inner controller managed steam/jacket dynamics, the PID outer controller was in charge of tracking the main temperature.
Behavior: The most complete controller, perfect for intricate or dynamic systems, such as reactor thermal dynamics.
Application: It is used in the temperature control system, especially for fast and precise correction in the outer loop of the cascade design.
- Comparison:
Table 2: Comparison of P, PI and PID controller
| Type | Pros | Cons |
| P | Simple, quick response | Steady state error |
| PI | No steady state error | Slower than P |
| PID | Accurate, fast setting | Sensitive to noise |
- Expected Reaction curves:
P: There is an offset but a quick climb.
PI: Rises more slowly but hits the setpoint precisely.
PID: No offset, little overshoot, and smooth response.
- Recommendations:
Level: PI controller for accuracy and ease of use in steady-state conditions.
Temperature: PI (inner) for cascade control and PID (outer).
You can download the Project files here: Download files now. (You must be logged in).
- Conclusion
The primary objective of this project was to develop and assess effective control strategies for modifying the temperature and level of a reactor system using MATLAB Simulink. I want to understand and compare the accuracy, stability, and disturbance rejection of several control techniques, including feedforward, cascade, open-loop, and single-loop feedback control systems. In order to study the behavior of natural systems, the simulation began with simple open-loop models. After that, feedback loops were included to enhance the simulation and eliminate steady-state errors. For level control, a PI controller was used in combination with feedforward compensation to handle disturbances such outflow changes [4]. To accurately control the reactor and jacket/steam temperatures, a more complex cascade PID-PI configuration was developed for temperature control [3]. Every system was described using realistic transfer functions, and scope results confirmed that performance increased with each new control strategy. The feedforward and cascade models showed better accuracy and response speed under various setpoint and disturbance conditions. The project’s overarching goals of creating and modeling dependable control systems, demonstrating their performance in real time in a process control scenario, and using dynamic modeling to validate theoretical concepts were all achieved.
- References
- J. Åström and R. M. Murray, “Feedback Systems: An Introduction for Scientists and Engineers,” Princeton University Press, 2010.
- Skogestad and I. Postlethwaite, “Multivariable Feedback Control: Analysis and Design,” 2nd ed., Wiley, 2005.
- Stephanopoulos, “Chemical Process Control: An Introduction to Theory and Practice,” Prentice Hall, 1984.
- Tan, D. Nesic and I. Mareels, “On non-local stability properties of extremum seeking control,” in IEEE Transactions on Automatic Control, vol. 53, no. 5, pp. 1244-1248, June 2008.
- Ogata, Modern Control Engineering, Fifth Edition, Prentice Hall, Upper Saddle River, NJ, USA, 2010.
Keywords: Controllers, level and temperature in a reactor, MATLAB design, MATLAB Simulink Model
You can download the Project files here: Download files now. (You must be logged in).









Responses