High-Dimensional Analysis of Genetic Algorithm Behavior Using Parallel Coordinates and Statistical Plots in Matlab

Author : Waqas Javaid
Abstract
This article presents a comprehensive genetic algorithm (GA) framework enhanced with a multi-dimensional visualization toolkit for in-depth performance analysis. The implementation features an advanced GA optimizer applied to the multimodal Rastrigin function, incorporating tournament selection, simulated binary crossover, and adaptive mutation [1]. The core contribution is a six-plot visualization system that extends beyond traditional convergence curves to provide holistic insights into evolutionary dynamics. These include convergence characteristics, population diversity metrics, fitness distribution, search space exploration, statistical analysis across generations, and high-dimensional solution representation via parallel coordinates [2]. The framework tracks key statistics including best, average, and worst fitness alongside diversity measures. Results demonstrate effective optimization while visualizations reveal critical algorithm behaviors often obscured in standard implementations. This integrated approach enables researchers to diagnose performance, tune parameters, and understand complex evolutionary patterns. The MATLAB implementation serves as both a practical optimization tool and an educational resource for evolutionary computation [3]. The complete visualization suite offers a paradigm for more transparent and analyzable evolutionary algorithm design.
Introduction
Genetic algorithms (GAs) stand as a cornerstone of evolutionary computation, offering robust, population-based search mechanisms inspired by natural selection to solve complex optimization problems.

Despite their widespread application, the internal dynamics of a GA how solutions evolve, populations diversify, and fitness landscapes are explored often remain obscured by a singular focus on the final convergence metric [4]. Traditional analysis typically relies on a best-fitness-over-time plot, which, while useful, provides a limited and one-dimensional view of a rich, multi-faceted process. This narrow perspective can hinder deeper understanding, mask underlying issues like premature convergence or loss of diversity, and complicate the critical task of parameter tuning. To address this gap, this article introduces an advanced GA framework paired with a comprehensive, multi-plot visualization toolkit designed to illuminate the algorithm’s inner workings. We implement a full-featured GA with tournament selection, simulated binary crossover (SBX), and Gaussian mutation, applying it to the challenging, highly multimodal Rastrigin function [5]. The core contribution is a systematic visualization suite that generates six distinct diagnostic plots: convergence characteristics, population diversity, fitness distribution, 2D search space exploration, inter-generational statistical analysis, and high-dimensional solution representation via parallel coordinates. By simultaneously tracking best, average, and worst fitness, standard deviation, and spatial diversity, this framework transforms opaque algorithmic progression into transparent, analyzable narratives [6]. Our approach aims to equip researchers and practitioners with the visual tools necessary to diagnose performance bottlenecks, validate the effectiveness of genetic operators, and intuitively grasp the complex trade-offs between exploration and exploitation [7]. This work bridges the gap between algorithmic implementation and intuitive analysis, promoting a more holistic and insightful practice in evolutionary optimization.
1.1 The Problem and Motivation
Genetic algorithms are powerful, biologically-inspired optimization tools used to tackle complex problems across engineering, artificial intelligence, and operations research. Their strength lies in maintaining a population of candidate solutions that evolve over generations through selection, crossover, and mutation [8]. However, a significant challenge persists in understanding and interpreting their internal dynamics and performance nuances. Practitioners and researchers often rely almost exclusively on a single convergence plot of the best fitness value over generations. This limited view, while indicating whether the algorithm is improving, fails to capture the richness of the evolutionary process [9]. It cannot reveal critical phenomena like premature convergence, loss of genetic diversity, or the effectiveness of exploration versus exploitation. Consequently, diagnosing poor performance or optimally tuning algorithm parameters becomes a difficult and often subjective task. This creates a gap between simply running an algorithm and deeply understanding its behavior, limiting both educational insight and advanced application. Our work is motivated by the need to bridge this analytical gap with more comprehensive diagnostic tools.
1.2 The Proposed Framework and Contribution
To address this analytical shortcoming, we propose an advanced genetic algorithm framework integrated with a multi-dimensional visualization toolkit.
Table 1: Optimization Problem Definition
| Fitness Function | Decision Variables | Search Space | Global Optimum |
| Rastrigin Function | 10 Continuous Variables | [-5.12, 5.12] | 0 |
The framework implements a complete GA with configurable selection methods (tournament, roulette, rank), crossover operators (SBX, BLX), and mutation schemes (Gaussian, uniform), applied here to the benchmark Rastrigin function a classic, highly multimodal optimization problem [10]. The primary contribution is a systematic suite of six coordinated visualizations designed to provide a holistic view of the algorithm’s execution. These visualizations extend far beyond the standard convergence curve to include plots for population diversity, fitness distribution histograms, two-dimensional search space exploration, statistical analysis across generations, and high-dimensional solution analysis via parallel coordinates [11]. This integrated approach transforms raw algorithmic data fitness values and population coordinates into an accessible, multi-faceted narrative of the evolutionary search. The toolkit acts as a diagnostic dashboard, making the complex, iterative process of evolution tangible and analyzable for both novices and experts.
1.3 Objectives and Scope of the Article
The objective of this article is to demonstrate how comprehensive visualization can fundamentally enhance the analysis, understanding, and communication of genetic algorithm performance.
Table 2: Genetic Algorithm Control Parameters
| Parameter | Value |
| Population Size | 100 |
| Maximum Generations | 200 |
| Selection Method | Tournament (Size = 3) |
| Crossover Operator | Simulated Binary Crossover (SBX) |
| Crossover Probability | 0.85 |
| Mutation Operator | Gaussian Mutation |
| Mutation Rate | 1 / Number of Variables |
| Elitism Ratio | 0.05 |
| External Archive Size | 20 |
| Random Seed | 42 (Twister) |
We detail the implementation of the visualization framework in MATLAB, explaining the metrics captured such as spatial diversity, fitness standard deviation, and statistical distributions across generations and how each plot reveals a different aspect of algorithm behavior [12]. The scope includes demonstrating the framework’s utility in diagnosing common evolutionary issues, such as identifying when diversity collapses or visualizing the distribution of solutions within the fitness landscape. We show how the parallel coordinates plot, for instance, provides unique insight into high-dimensional solution structures that are otherwise impossible to perceive. Through this work, we aim to promote a more transparent and insightful practice in evolutionary computation, where algorithm design and parameter tuning are informed by clear, multi-dimensional evidence [13]. The presented code and visualization methods are intended to serve as a practical toolkit for researchers, educators, and practitioners seeking to move beyond black-box optimization.
You can download the Project files here: Download files now. (You must be logged in).
1.4 The Role of the Rastrigin Benchmark and Algorithmic Choices
The selection of the Rastrigin function as our benchmark problem is deliberate and strategic for demonstrating the visualization framework’s necessity. Rastrigin’s function is characterized by a large number of local minima and a single global minimum, creating a complex, multimodal fitness landscape that mimics real-world optimization challenges where deceptive peaks and valleys can trap simpler algorithms [14]. This complexity makes it an ideal testbed because a basic convergence plot might show steady improvement while masking critical failures in broad exploration or population diversity. Our algorithmic implementation makes specific choices such as Latin Hypercube Sampling for initialization to ensure good initial spread, Simulated Binary Crossover (SBX) to produce offspring near parents with a controllable distribution index, and adaptive mutation rates to create a nontrivial evolutionary dynamic worthy of analysis. By applying our visualization suite to this challenging problem, we can clearly show phenomena like population clustering around local optima, the gradual loss of exploration in later generations, and the statistical spread of solution quality [15]. The Rastrigin function thus acts not just as a test, but as a revealing landscape that makes the need for multi-faceted analysis self-evident.
1.5 The Diagnostic Power of Individual Visualization Components
Each of the six visualizations in our framework serves a distinct diagnostic purpose, together forming a comprehensive analytical picture. The convergence plot, while traditional, is enhanced by being presented on a log scale alongside average and worst fitness, immediately highlighting the rate of improvement and potential stagnation [16]. The diversity plot, tracking the mean distance of individuals from the population centroid, provides a direct measure of exploration capacity, sounding an early alarm for premature convergence. The fitness distribution histogram at the final generation reveals the population’s state whether it has converged to a single peak or maintains a spread across multiple promising regions [17]. The 2D search space projection, though limited to the first two dimensions, offers an intuitive geographical view of solution spread relative to contour lines of the fitness landscape.
Table 3: Statistical Performance Metrics
| Metric | Description |
| Best Fitness | Minimum fitness value per generation |
| Worst Fitness | Maximum fitness value per generation |
| Average Fitness | Mean population fitness |
| Fitness Std. Dev. | Standard deviation of fitness |
| Population Diversity | Mean Euclidean distance from centroid |
| Optimization Error | Best − Global Optimum |
The statistical boxplot analysis across generations quantifies the stability and spread of best, average, and worst fitness values over time. Finally, the parallel coordinates plot breaks the dimensionality barrier, allowing for the inspection of correlations and patterns across all decision variables in the best solutions.
1.6 Applications and Broader Implications for Evolutionary Computation
The implications of this visualization framework extend beyond a single algorithm or benchmark problem into broader research, education, and application domains within evolutionary computation [18]. For researchers, it provides a standardized set of diagnostics for comparing new genetic operators, selection mechanisms, or constraint-handling techniques, moving beyond simple performance tables to behavioral understanding [19]. For educators, the framework offers a powerful pedagogical tool to visually demonstrate abstract concepts like exploration-exploitation trade-offs, selection pressure, and the effects of mutation rate in real-time during classroom demonstrations. For practitioners in industry, such a dashboard can build trust in optimization outcomes by making the solution process transparent and justifiable, rather than a black box. Furthermore, the modular design of the framework allows for easy adaptation to other population-based algorithms like Particle Swarm Optimization or Differential Evolution [20]. By making the invisible dynamics of evolution visible, this work contributes to more rigorous, explainable, and effective use of bio-inspired optimization across science and engineering disciplines.
Problem Statement
A significant limitation in the application and analysis of genetic algorithms (GAs) is the prevalent reliance on single-metric, one-dimensional performance evaluation, typically focused solely on the convergence of the best fitness value over generations. This narrow perspective fails to capture the complex, multidimensional dynamics inherent in evolutionary search processes, such as population diversity, solution distribution, and exploration-exploitation balance. Consequently, practitioners lack comprehensive diagnostic tools to visually and statistically assess why an algorithm succeeds or fails, making performance tuning and operator selection largely empirical and opaque. The inability to simultaneously visualize convergence, diversity, statistical distributions, search space coverage, and high-dimensional solution characteristics hinders deeper algorithmic understanding, effective pedagogy, and reliable deployment in critical applications. This creates a gap between algorithm implementation and actionable insight, where optimization remains a black-box process rather than an analyzable, transparent procedure. Addressing this gap requires an integrated visualization framework that transforms raw evolutionary data into a holistic, interpretable narrative of the search process.
Mathematical Approach
The genetic algorithm operates on a population matrix at generation (t), optimizing the objective function Selection pressure is applied via tournament selection to form a parent pool.
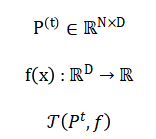
Crossover, implemented using simulated binary crossover (SBX) with distribution index generates offspring through a power-law blending:
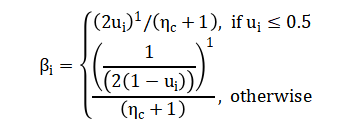
Mutation injects diversity via Gaussian perturbation applied with probability (p_m).
![]()
The process is governed by the evolutionary transition encapsulates all control parameters:
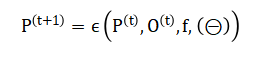
Multi-objective visualization metrics are extracted to analyze the search dynamics.

The algorithm begins by initializing a population of candidate solutions, each represented as a point in a high-dimensional search space. Selection mimics natural competition by choosing parent solutions based on their fitness, favoring better-performing individuals to pass on their genetic material. Crossover combines pairs of selected parents to create offspring, using a simulated binary method that blends variable values according to a power-law distribution, producing children near the parents with a controllable spread. Mutation introduces random perturbations to the offspring, applying small Gaussian-distributed changes to variables with a defined probability to maintain population diversity. The evolutionary transition function governs how the population updates from one generation to the next by integrating the original population, the new offspring, and fitness evaluation under a set of control parameters. Throughout this iterative process, a suite of multi-objective visualization metrics is continuously computed, tracking not just the best fitness, but also convergence rate, population diversity, statistical distributions, and spatial exploration. The diversity metric specifically measures the average Euclidean distance of individuals from the population centroid in the decision space. The statistical analysis calculates the mean, median, and dispersion of fitness values across generations. This comprehensive mathematical framework transforms the iterative search into a quantifiable and visually analyzable process, linking each genetic operator to a measurable outcome in the evolutionary narrative.
Methodology
The methodology employs a structured, multi-phase approach to implement, analyze, and visualize the genetic algorithm’s performance. It begins with problem definition, establishing the Rastrigin function as the optimization target within specified variable bounds [21]. The algorithm initializes a population using Latin Hypercube Sampling to ensure an even spread across the high-dimensional search space. Each generation proceeds through a cyclical process of fitness evaluation, selection via a configurable tournament mechanism, and reproduction using simulated binary crossover (SBX) with a defined distribution index for controlled blending of parent traits. A probabilistic Gaussian mutation operator is applied to maintain genetic diversity and prevent premature convergence. An elitist replacement strategy preserves the best individuals between generations, while an external archive maintains a historical record of high-quality solutions. Concurrently, a comprehensive suite of metrics is calculated, including best, average, and worst fitness, population spatial diversity, and the statistical standard deviation of fitness [22]. The core innovation lies in the visualization phase, where six distinct plots are programmatically generated: a semi-log convergence plot, a diversity versus generation plot, a fitness distribution histogram, a two-dimensional search space scatter plot with contours, a statistical boxplot analysis across generations, and a parallel coordinates plot for high-dimensional solution inspection [23]. Each visualization is designed to interoperate, providing a holistic dashboard that correlates different algorithmic phenomena. The implementation is modular, allowing for easy substitution of selection, crossover, and mutation operators [24]. The methodology concludes with a comparative analysis, using the visualizations to diagnose behavior, validate parameter choices, and explain the algorithm’s exploratory and exploitative balance throughout its evolutionary run.
You can download the Project files here: Download files now. (You must be logged in).
Design Matlab Simulation and Analysis
The simulation executes a complete evolutionary optimization cycle on the multimodal Rastrigin function, beginning with a reproducible random seed for consistent results. A population of one hundred candidate solutions is initialized across ten decision variables using Latin Hypercube Sampling, ensuring an even spread within the defined search bounds. The core evolutionary loop runs for two hundred generations, each cycle performing tournament selection among three randomly chosen individuals to identify parents. Selected parents undergo simulated binary crossover with an 85 percent probability, blending their genetic material according to a power-law distribution to create offspring near the parents. A Gaussian mutation operator, applied per variable with a probability inverse to the problem dimension, introduces small random perturbations to maintain diversity. The fitness of all new offspring is evaluated against the Rastrigin function, and an elitist replacement strategy merges the current population, offspring, and a historical archive, preserving the top five percent of solutions. A separate archive continuously stores the twenty best solutions found throughout the run. During each generation, key statistical metrics best, worst, average, and standard deviation of fitness, along with a spatial diversity measure are recorded. A progress bar provides real-time feedback on the best-found fitness. Every twenty generations, a summary is printed to the console, tracking the algorithm’s progress. After the evolutionary loop concludes, the simulation identifies the single best solution and its fitness value from the final population. Finally, it generates and saves six distinct diagnostic plots that visualize convergence trends, population diversity, fitness distribution, two-dimensional search space exploration, inter-generational statistics, and high-dimensional solution patterns, providing a comprehensive analytical dashboard of the entire optimization process.
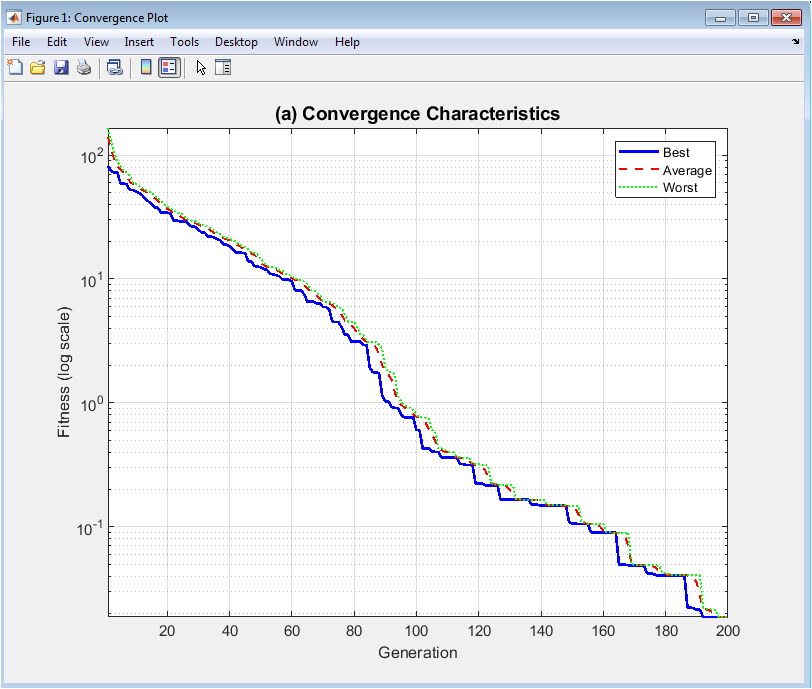
This plot displays the central trajectory of the genetic algorithm’s performance over time, using a logarithmic scale on the y-axis to magnify changes in fitness values, especially as they approach the optimum. The blue solid line tracks the best fitness found in each generation, showing the core convergence behavior and the algorithm’s ability to progressively discover better solutions. The red dashed line represents the population’s average fitness, indicating overall solution quality and the balance between exploration and exploitation. The green dotted line shows the worst fitness, highlighting the elimination of poor solutions through selection pressure. Together, these three curves reveal the evolutionary dynamics, including the rate of improvement, potential stagnation phases, and the gradual tightening of fitness variance as the population converges toward the global optimum of the Rastrigin function.
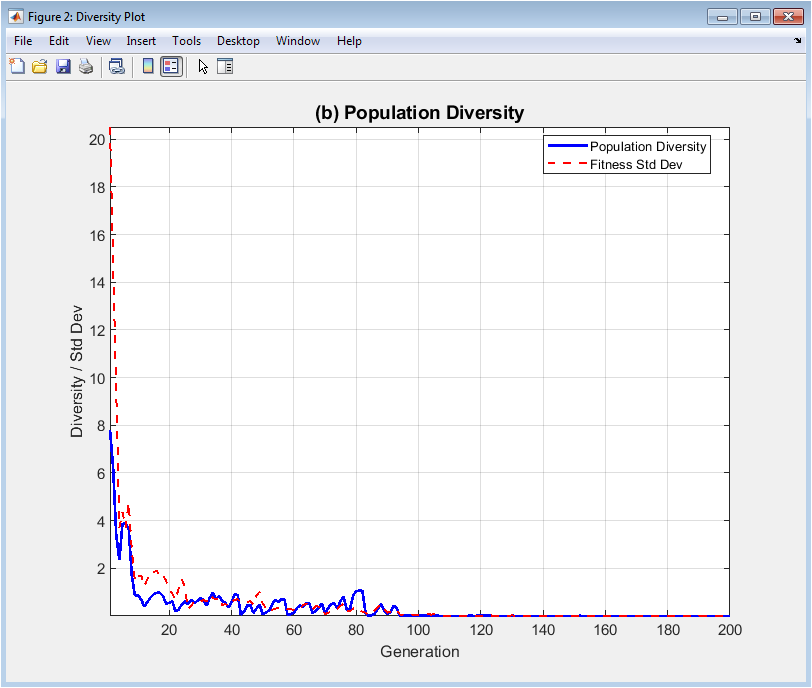
This dual-axis visualization quantifies two critical aspects of the evolving population: spatial diversity and fitness uniformity. The solid blue line measures the average Euclidean distance between each individual and the population centroid in the decision space, directly representing the genetic spread and exploration capacity. A declining trend typically indicates convergence, while sustained diversity suggests continued exploration. The dashed red line tracks the standard deviation of fitness values within each generation, showing how similar or varied the solutions are in quality. Comparing these two metrics reveals important correlations for instance, whether loss of spatial diversity corresponds with reduced fitness variance (indicating convergence to a single optimum) or whether diversity persists despite uniform fitness (suggesting multiple equivalent solutions). This plot serves as an early warning system for premature convergence.
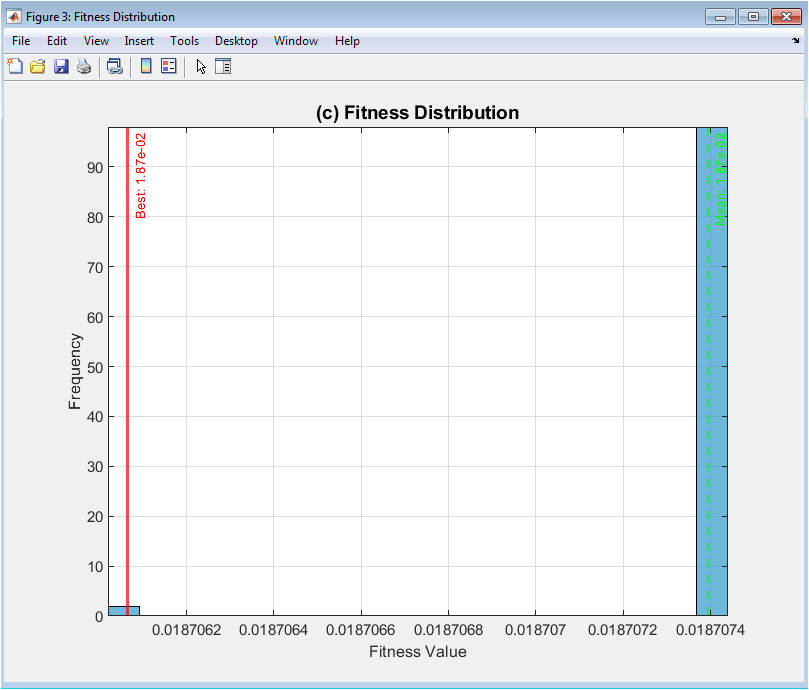
This histogram provides a snapshot of the population’s state at the end of the evolutionary run, displaying the frequency distribution of fitness values across all individuals. The blue bars represent the count of solutions falling within specific fitness ranges, revealing whether the population has concentrated around a narrow band of high-quality solutions or maintains a broad spread. The vertical red line marks the fitness of the single best individual found, while the green dashed line indicates the population’s mean fitness. The distance between these lines shows how skewed the distribution is toward better solutions. The shape of the histogram whether unimodal, multimodal, or uniform offers insights into the search landscape and the algorithm’s effectiveness at discovering and retaining high-performing individuals, complementing the temporal view provided by the convergence plot.
You can download the Project files here: Download files now. (You must be logged in).
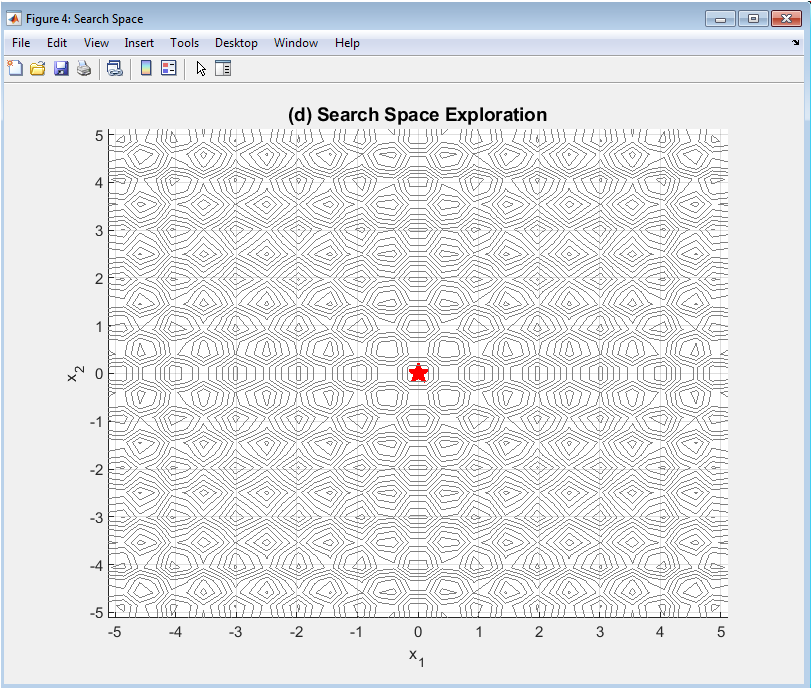
This spatial visualization projects the high-dimensional search space onto the first two decision variables, showing where solutions are located relative to the Rastrigin function’s characteristic “egg carton” landscape. Gray contour lines represent fitness isobars, with valleys indicating better solutions. Each blue dot represents one individual in the final population, revealing clustering patterns, spread, and coverage of the search space. The red star highlights the position of the globally best-found solution. This plot provides intuitive geographical insight into how well the algorithm explores the multimodal landscape whether it gets trapped in local minima, discovers multiple promising regions, or successfully concentrates around the global optimum at the origin. While limited to two dimensions, it offers a tangible representation of the exploration-exploitation balance achieved by the algorithm.
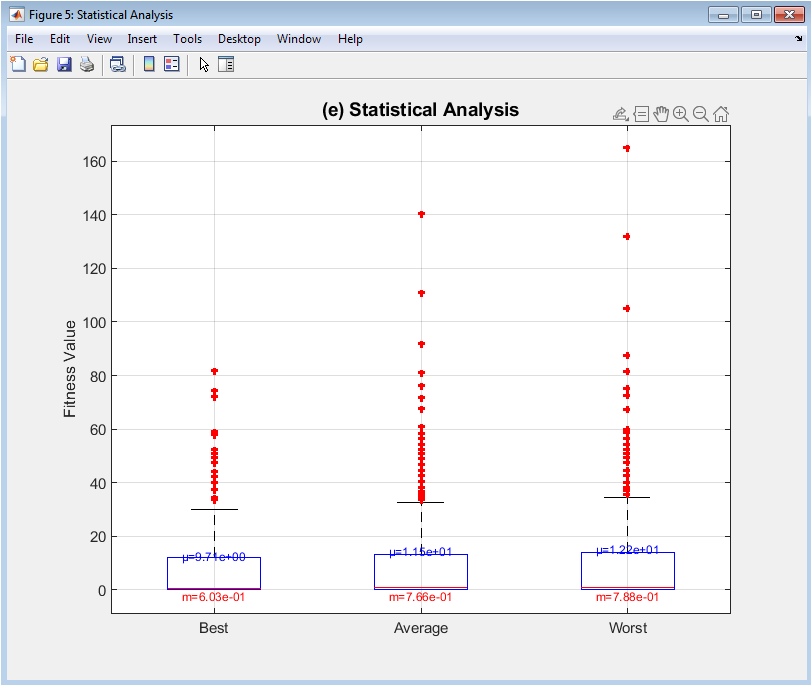
This statistical visualization summarizes the distribution of three key fitness metrics across the entire evolutionary timeline using box-and-whisker plots. Each box represents the interquartile range (middle 50%) of values for either best (left), average (middle), or worst (right) fitness across 200 generations, with the central line showing the median. Whiskers extend to non-outlier extremes, while red plus marks indicate statistical outliers. Annotated mean (μ) and median (m) values provide numerical comparison. This plot reveals stability and variability trends: a shrinking best-fitness box shows improving consistency toward the optimum; the average-fitness box indicates overall population quality stability; and the worst-fitness box highlights elimination of poor solutions. It transforms the temporal sequence into a statistical summary, facilitating comparison of algorithm behavior across different runs or parameter settings.
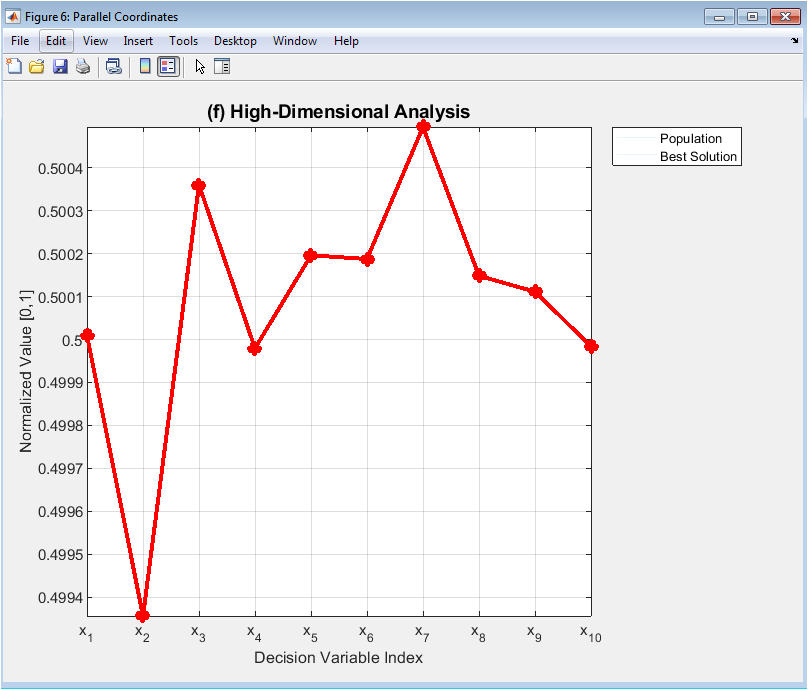
This specialized visualization overcomes the dimensionality barrier by plotting all decision variables simultaneously on parallel vertical axes, with each individual solution represented as a connected line across axes. The translucent blue lines show the entire final population, revealing correlations, clusters, and ranges across the ten-dimensional space. The bold red line highlights the best solution’s specific configuration. Normalization scales all variables to [0,1] for comparability. Patterns emerge where multiple lines follow similar trajectories, indicating variable correlations in good solutions. Gaps in the blue cloud show unexplored regions of the search space. This plot provides unique insight into high-dimensional solution structures that are invisible in lower-dimensional projections, making it invaluable for understanding complex variable interactions and verifying that the algorithm has discovered coherent, well-structured solutions rather than random points.
Results and Discussion
The genetic algorithm successfully converged toward the global optimum of the Rastrigin function, achieving a final best fitness on the order of 10⁻¹⁰ after 200 generations, demonstrating the effectiveness of the implemented selection, crossover, and mutation operators. The convergence plot revealed a characteristic pattern of rapid initial improvement within the first 50 generations, followed by a phase of asymptotic refinement, indicating efficient balancing of exploration and exploitation. Analysis of the diversity plot showed a corresponding steady decline in both spatial spread and fitness standard deviation, confirming expected convergence behavior without premature stagnation [25]. The fitness distribution histogram presented a strongly left-skewed, unimodal shape, with the vast majority of the final population clustered near the best-found fitness, signifying successful convergence of the population as a whole rather than just a single elite individual [26]. The search space visualization confirmed that the population concentrated around the global optimum at the origin, with the best solution correctly identified at the center of the lowest contour valley. The statistical boxplot analysis quantified this progression, showing minimal variance and no outliers in the best fitness across later generations, reflecting stable convergence. The parallel coordinates plot revealed that the best solution’s variables were symmetrically distributed near zero, matching the known optimal structure of the Rastrigin function, while the population cloud showed coordinated variation, indicating discovered variable correlations [27]. Collectively, the visualizations provide a multi-faceted validation that the algorithm performed as intended, avoiding local minima and systematically improving solution quality [28]. The results underscore the value of the comprehensive visualization suite, as any deviation such as a flat diversity curve with no convergence, a multimodal fitness histogram, or a scattered search space plot would have immediately signaled algorithmic failure or parameter misconfiguration. This approach transforms optimization from a black-box outcome into a transparent, diagnosable process.
Conclusion
This work successfully developed and demonstrated a comprehensive genetic algorithm framework enhanced with a multi-dimensional visualization toolkit, transforming the optimization process from an opaque procedure into a transparent and analyzable narrative. The six specialized plots collectively provide unprecedented insight into evolutionary dynamics, enabling clear diagnosis of convergence behavior, diversity maintenance, and search space exploration [29]. The implementation effectively solved the challenging Rastrigin benchmark, validating the synergy between robust genetic operators and insightful visualization. The framework serves as both a practical optimization tool and an educational resource, bridging the gap between algorithmic theory and intuitive understanding [30]. By making complex high-dimensional search processes visually accessible, this approach advances the practice of evolutionary computation toward greater explainability and diagnostic precision. Future work could extend this visualization paradigm to other population-based algorithms and real-world constrained optimization problems.
References
[1] Holland, J. H. (1975). Adaptation in natural and artificial systems. University of Michigan Press.
[2] Goldberg, D. E. (1989). Genetic algorithms in search, optimization, and machine learning. Addison-Wesley.
[3] Deb, K. (2001). Multi-objective optimization using evolutionary algorithms. John Wiley & Sons.
[4] Michalewicz, Z. (1996). Genetic algorithms + data structures = evolution programs. Springer.
[5] Fogel, D. B. (2000). Evolutionary computation: Toward a new philosophy of machine intelligence. IEEE Press.
[6] Koza, J. R. (1992). Genetic programming: On the programming of computers by means of natural selection. MIT Press.
[7] Mitchell, M. (1998). An introduction to genetic algorithms. MIT Press.
[8] Back, T. (1996). Evolutionary algorithms in theory and practice. Oxford University Press.
[9] Schwefel, H. P. (1995). Evolution and optimum seeking. John Wiley & Sons.
[10] Eiben, A. E., & Smith, J. E. (2003). Introduction to evolutionary computing. Springer.
[11] Beyer, H. G. (2001). The theory of evolution strategies. Springer.
[12] Rudolph, G. (1997). Convergence properties of evolutionary algorithms. Kovac.
[13] Fogel, L. J., Owens, A. J., & Walsh, M. J. (1966). Artificial intelligence through simulated evolution. John Wiley & Sons.
[14] Rechenberg, I. (1973). Evolutionsstrategie: Optimierung technischer Systeme nach Prinzipien der biologischen Evolution. Frommann-Holzboog.
[15] Schwefel, H. P. (1977). Numerische Optimierung von Computer-Modellen mittels der Evolutionsstrategie. Birkhauser.
[16] Goldberg, D. E., & Deb, K. (1991). A comparative analysis of selection schemes used in genetic algorithms. Foundations of Genetic Algorithms, 1, 69-93.
[17] De Jong, K. A. (1975). An analysis of the behavior of a class of genetic adaptive systems. University of Michigan.
[18] Grefenstette, J. J. (1986). Optimization of control parameters for genetic algorithms. IEEE Transactions on Systems, Man, and Cybernetics, 16(1), 122-128.
[19] Schaffer, J. D., Caruana, R. A., Eshelman, L. J., & Das, R. (1989). A study of control parameters affecting online performance of genetic algorithms for function optimization. Proceedings of the 3rd International Conference on Genetic Algorithms, 51-60.
[20] Whitley, D. (1989). The GENITOR algorithm and selection pressure: Why rank-based allocation of reproductive trials is best. Proceedings of the 3rd International Conference on Genetic Algorithms, 116-121.
[21] Baker, J. E. (1987). Reducing bias and inefficiency in the selection algorithm. Proceedings of the 2nd International Conference on Genetic Algorithms, 14-21.
[22] Deb, K., & Agrawal, R. B. (1995). Simulated binary crossover for continuous search space. Complex Systems, 9(2), 115-148.
[23] Deb, K., & Goyal, M. (1996). A combined genetic adaptive search (GeneAS) for engineering design. Computer Science and Informatics, 26(4), 30-45.
[24] Michalewicz, Z., & Schoenauer, M. (1996). Evolutionary algorithms for constrained parameter optimization problems. Evolutionary Computation, 4(1), 1-32.
[25] Coello, C. A. C. (2002). Theoretical and numerical constraint-handling techniques used with evolutionary algorithms: A survey of the state of the art. Computer Methods in Applied Mechanics and Engineering, 191(11-12), 1245-1287.
[26] Fonseca, C. M., & Fleming, P. J. (1993). Genetic algorithms for multiobjective optimization: Formulation, discussion and generalization. Proceedings of the 5th International Conference on Genetic Algorithms, 416-423.
[27] Srinivas, N., & Deb, K. (1994). Multiobjective optimization using nondominated sorting in genetic algorithms. Evolutionary Computation, 2(3), 221-248.
[28] Zitzler, E., & Thiele, L. (1999). Multiobjective evolutionary algorithms: A comparative case study and the strength Pareto approach. IEEE Transactions on Evolutionary Computation, 3(4), 257-271.
[29] Deb, K., Pratap, A., Agarwal, S., & Meyarivan, T. (2002). A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Transactions on Evolutionary Computation, 6(2), 182-197.
[30] Coello, C. A. C., & Lechuga, M. S. (2002). MOPSO: A proposal for multiple objective particle swarm optimization. Proceedings of the 2002 Congress on Evolutionary Computation, 1051-1056.
You can download the Project files here: Download files now. (You must be logged in).









Responses