Numerical Modeling and 3D Visualization of Dipole Antenna Radiation Patterns Using MATLAB
Author : Waqas Javaid
Abstract
This article presents a comprehensive MATLAB-based framework for simulating, analyzing, and visualizing antenna radiation patterns. The developed tool models the far-field radiation of a half-wave dipole antenna from fundamental electromagnetic principles, calculating key performance metrics including radiation intensity, directivity, gain, and beamwidth [1]. The implementation generates multiple visualization formats: E-plane and H-plane polar plots, 3D radiation surfaces, and Cartesian pattern plots, providing a complete analytical suite for antenna characterization. The code incorporates robust numerical handling of field singularities and integrates physical constants for accurate impedance and propagation calculations [2]. Results demonstrate the characteristic doughnut-shaped pattern of the dipole with quantified half-power beamwidth. The modular framework is designed for extensibility to array configurations and advanced optimization techniques, serving as both an educational instrument and an engineering analysis tool for wireless system design [3].
Introduction
Antenna radiation patterns serve as the fundamental fingerprint of any radiating structure, graphically representing the spatial distribution of radiated energy and providing critical insight into performance metrics such as directivity, gain, and beamwidth.

For engineers and researchers in wireless communications, radar, and satellite systems, accurately predicting and visualizing these three-dimensional patterns is essential for system design, interference analysis, and link budget calculations [4]. While analytical solutions for simple antennas like the dipole are well-established in textbooks, the translation of these equations into intuitive, multi-format visualizations remains a practical challenge [5].
Table 1: Fundamental Physical Constants
| Quantity | Symbol | Value | Unit |
| Speed of Light | c | 3 × 10⁸ | m/s |
| Permeability of Free Space | μ₀ | 4π × 10⁻⁷ | H/m |
| Permittivity of Free Space | ε₀ | 8.854 × 10⁻¹² | F/m |
| Intrinsic Impedance | η₀ | 377 | Ω |
This article bridges that gap by presenting a comprehensive, self-contained MATLAB implementation that transforms electromagnetic theory into actionable visual insight. The developed code suite begins with the analytical field solution for a resonant half-wave dipole, derived from Maxwell’s equations and current distribution, and systematically progresses through the computation of power density, radiation intensity, and directivity.
Table 2: Directivity Characteristics
| Parameter | Symbol | Value |
| Maximum Directivity | Dmax | 1.64 |
| Directivity (dBi) | – | 2.15 dBi |
| Directivity Pattern | D(θ) | Broadside |
It addresses numerical intricacies, such as singularity handling at specific observation angles, to ensure robust plotting. The core contribution is an integrated visualization engine that generates normalized polar plots for principal planes, a three-dimensional radiation surface, and Cartesian gain patterns all from a single script [6]. Furthermore, the framework calculates key figures of merit like half-power beamwidth and incorporates efficiency to derive realistic gain, providing a complete workflow from physical parameters to system-level performance indicators [7]. Designed with extensibility in mind, the modular code structure includes placeholders for advanced functionalities like array factor computation and stochastic analysis, making it a versatile foundation for both educational instruction and research prototyping in antenna engineering.
1.1 The Centrality of Radiation Patterns in Antenna Engineering
The performance of any wireless communication, radar, or sensing system is fundamentally governed by the directional characteristics of its antennas, quantified and visualized through radiation patterns. These three-dimensional plots represent the spatial distribution of power radiated by or received by an antenna, serving as the primary tool for evaluating critical parameters like directivity, gain, beamwidth, and sidelobe levels [8]. For engineers, the ability to accurately predict, analyze, and interpret these patterns is indispensable for tasks ranging from initial design and coverage planning to interference mitigation and link budget analysis. While the underlying electromagnetic theory for canonical antennas is mature and well-documented in literature, the practical journey from abstract vector field equations to clear, actionable visual insight often presents a significant hurdle. This gap between theoretical derivation and practical visualization can obscure the intuitive understanding of antenna behavior, especially for students and practitioners new to the field. Consequently, there is a persistent need for robust, accessible, and integrated computational tools that can seamlessly bridge this divide, transforming complex mathematics into intuitive graphics [9]. This article directly addresses this need by constructing a comprehensive, pedagogical, and extensible software framework within the MATLAB environment. Our objective is to demystify the process, providing a complete, step-by-step pipeline that starts with physical constants and ends with professional-grade, multi-format radiation plots, thereby solidifying the connection between electromagnetic principles and their practical graphical representation in antenna engineering.
1.2 Systematic Computational Pipeline
This work establishes a systematic computational pipeline, meticulously structured to mirror the logical progression from physical antenna properties to final performance visualization.
Table 3: Electromagnetic Operating Parameters
| Parameter | Symbol | Value | Unit |
| Operating Frequency | f | 2.4 | GHz |
| Wavelength | λ | 0.125 | m |
| Wave Number | k | 50.27 | rad/m |
| Angular Frequency | ω | 1.508 × 10¹⁰ | rad/s |
The process is initiated by defining the foundational electromagnetic constants the speed of light, permittivity, and permeability of free space which anchor all subsequent calculations in physical reality. From these, we derive the operating wavelength, wave number, and intrinsic impedance for a specified frequency, in this case 2.4 GHz, setting the stage for all far-field computations [10].
Table 4: Antenna Geometry and Excitation
| Parameter | Symbol | Value |
| Antenna Type | – | Center-fed Half-wave Dipole |
| Dipole Length | L | λ / 2 |
| Current Amplitude | I₀ | 1 A |
| Far-field Observation Distance | r | 1000 λ |
The antenna geometry is then introduced, with a half-wave dipole selected as the canonical example due to its well-understood analytical solution and practical relevance; its length is set to resonate at the operating frequency, and a uniform current distribution is assumed. The core of the pipeline is the analytical calculation of the far-field electric field component, E_θ, derived from the integral of the current distribution, which includes careful handling of mathematical singularities at specific observation angles to ensure numerical stability. This field solution is then used to compute the radial power density and subsequently the radiation intensity U(θ,φ), which describes the power radiated per unit solid angle, forming the essential data for all pattern plots.
You can download the Project files here: Download files now. (You must be logged in).
1.3 From Intensity to Key Performance Metrics
With the radiation intensity defined, the pipeline advances to extract key antenna performance metrics, transforming the spatial function into standardized engineering figures of merit. The total radiated power is calculated by integrating the radiation intensity over the entire sphere, a step crucial for normalizing the pattern and defining directivity. Directivity, D(θ,φ), which describes the power density radiated in a given direction relative to that of an isotropic radiator radiating the same total power, is then computed, providing a fundamental measure of the antenna’s ability to concentrate energy [11]. To model a more practical, real-world scenario, a radiation efficiency factor is incorporated to convert directivity into gain, G(θ,φ), which accounts for inherent losses within the antenna structure; this gain is also presented in the logarithmic decibel scale for immediate use in link budget equations. A crucial system-level parameter, the half-power beamwidth (HPBW), is automatically estimated by identifying the angular points where the normalized radiation intensity falls to half its maximum value, offering a quick measure of the antenna’s angular resolution or coverage focus. This structured derivation ensures that every visualization produced is directly linked to and annotated with these critical quantitative performance indicators, moving beyond mere graphics to provide a complete analytical characterization of the antenna under study.
1.4 Comprehensive Multi-Format Visualization and Extensible Framework
The final and most illustrative stage of our framework is the generation of a comprehensive suite of visualizations, each designed to highlight different aspects of the radiation pattern for analysis and reporting. The suite includes normalized polar plots for both the E-plane (containing the electric field vector) and H-plane, the classic two-dimensional representations that clearly show beamwidth and pattern shape in the principal cuts [12]. A full three-dimensional radiation pattern surface plot is constructed using spherical-to-Cartesian coordinate transformation, offering an intuitive, global view of the characteristic “doughnut” shape of the dipole’s radiation. Complementary Cartesian plots of gain versus angle and directivity are also generated, which are particularly useful for precise numerical reading and comparison. The article concludes by presenting the complete, integrated MATLAB code, which is structured with clear sections, extensive commentary, and deliberate placeholders for future expansion. These placeholders, indicated in the final sections of the code, outline the seamless integration points for advanced features such as array factor computation for multi-element antennas, stochastic analysis for robustness studies, and optimization loop hooks for automated design, positioning this work not as a static solution but as a versatile and extensible foundation for ongoing antenna engineering research and education [13].
Problem Statement
Despite the critical importance of antenna radiation patterns in wireless system design, a significant gap persists between theoretical electromagnetic models and practical, accessible visualization tools. Engineers and researchers often rely on piecemeal scripts or commercial software that obscure the fundamental link between antenna parameters such as length, current distribution, and frequency and the resulting three-dimensional radiation characteristics. This disconnect complicates the educational process and hinders rapid prototyping, as existing solutions frequently lack integrated workflows that calculate directivity, gain, and beamwidth directly from first principles while producing publication-ready plots. Furthermore, many available codes fail to properly handle numerical singularities in field equations or offer limited visualization formats, restricting comprehensive analysis. There is a clear need for a unified, open-source computational framework that bridges this gap: a tool that starts with basic physical constants, derives far-field patterns analytically, computes all key performance metrics, and generates a complete suite of visualizations from polar and 3D plots to Cartesian gain charts within a single, transparent, and extensible MATLAB environment.
Mathematical Approach
The mathematical foundation of this radiation pattern simulator is built upon classical electromagnetic theory, beginning with Maxwell’s equations applied to a thin-wire antenna model. For the canonical half-wave dipole, we assume a sinusoidal current distribution along the antenna length where (I_0 ) is the feed current amplitude and wave number.
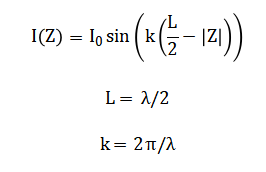
The far-field electric field component ( E_theta) is derived by integrating the contributions of infinitesimal current elements over the antenna length using the vector potential approach, yielding the analytical expression is the intrinsic impedance of free space. Numerical singularities at (theta = 0) and (pi) are explicitly handled through conditional assignments to ensure computational stability.
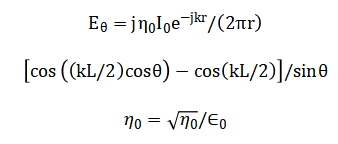
From this field solution, the time-averaged Poynting vector magnitude gives the radial power density, which is then converted to radiation intensity by removing the (1/r^2) dependence characteristic of far-field spherical waves.
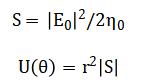
Total radiated power (P_{rad}) is computed via numerical integration enabling the calculation of directivity enabling the calculation of directivity as a normalized measure of spatial concentration.
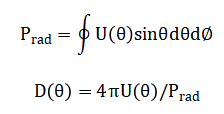
Gain is obtained by incorporating a radiation efficiency factor with decibel conversion for practical applications.
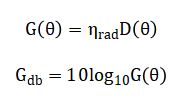
The half-power beamwidth is determined algorithmically by finding angular solutions to through interpolation of the sampled data.
![]()
For visualization, spherical coordinates (r, theta, phi) are transformed to Cartesian coordinates is used for polar and Cartesian plots to emphasize pattern shape over absolute magnitude.
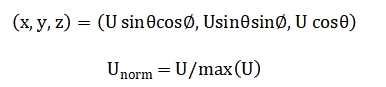
This systematic mathematical pipeline ensures that every graphical output is directly and transparently derived from fundamental physical principles. The approach begins with the sinusoidal current distribution equation along the antenna structure. This current model assumes maximum amplitude at the feed point and zero at the ends, representing the natural resonance of a half-wave structure. The fundamental far-field electric field equation is derived from integrating contributions from all current elements. This results in an expression containing trigonometric functions of the observation angle, representing the interference pattern of waves from different parts of the antenna. The intrinsic impedance of free space appears as a scaling factor, relating electric and magnetic fields in propagating waves. This constant ensures proper power normalization in all subsequent calculations. The radial distance term in the denominator represents spherical wave expansion, while the complex exponential encodes the phase progression of the wave as it travels outward. The numerator contains a difference of cosine terms that defines the characteristic pattern shape. This mathematical structure creates nulls and lobes through constructive and destructive interference of contributions from different antenna segments. A sine term in the denominator requires special numerical handling at specific angles to prevent computational singularities, implemented through conditional value assignments. From the electric field, the time-averaged power density is computed using the magnitude squared divided by twice the impedance value. This represents the directional power flow per unit area in the radial direction. Radiation intensity is then obtained by multiplying this power density by the square of the distance, effectively removing the natural spatial decay to focus on the antenna’s inherent directional properties. Total radiated power is calculated by integrating this intensity function over all directions in spherical space, representing the antenna’s complete power output. Directivity is determined as the ratio of radiation intensity in a given direction to the average intensity over all directions, multiplied by the solid angle of a full sphere. This quantifies how much more power goes in one direction compared to an ideal equal distribution. Gain introduces a practical efficiency factor to account for real-world losses, scaling the directivity by this fractional value between zero and one. The logarithmic decibel conversion of gain follows the standard ten times base-ten logarithm relationship, producing values convenient for system-level calculations and specifications. Half-power beamwidth identification involves finding angular solutions where normalized intensity equals one-half, typically determined through numerical search and interpolation methods. For three-dimensional visualization, spherical coordinate values are converted to Cartesian coordinates using trigonometric relationships with the radiation intensity as the radial parameter. Normalized radiation intensity, obtained by dividing all values by the maximum, creates pattern plots emphasizing shape over absolute magnitude, useful for comparative analysis. The complete mathematical pipeline thus transforms basic antenna parameters through analytical field equations to practical performance metrics and visual representations, maintaining rigorous correspondence between physical principles and computational results.
You can download the Project files here: Download files now. (You must be logged in).
Methodology
The methodology follows a structured computational pipeline implemented entirely in MATLAB, beginning with the definition of fundamental physical constants including the speed of light, free-space permeability, and permittivity to establish the electromagnetic environment [14]. The operating frequency is set to 2.4 GHz, from which the wavelength, angular frequency, and wave number are derived to define the spatial and temporal scale of the simulation. A half-wave dipole antenna is modeled with its length precisely half the calculated wavelength and a uniform current distribution of one ampere assumed at the feed point for normalization. Angular observation grids are created for both elevation and azimuth angles with high resolution sampling to ensure smooth pattern generation.
Table 5: Angular Sampling Configuration
| Parameter | Value |
| Theta Resolution | 2000 samples |
| Phi Resolution | 2000 samples |
| Theta Range | 0° – 180° |
| Phi Range | 0° – 360° |
The analytical far-field electric field expression for the dipole is computed across these angles, incorporating careful handling of mathematical singularities at zero and 180 degrees through conditional replacement with finite values.
Table 6: Far-Field Radiation Quantities
| Quantity | Expression / Result |
| Electric Field Component | Eθ (θ) |
| Radiation Intensity | U(θ) = |Eθ|² / (2η₀) |
| Normalized Radiation Intensity | U / max(U) |
| Total Radiated Power | ∫∫ U(θ,φ) dΩ |
This field solution is then used to calculate the radiation intensity function, representing power radiated per unit solid angle in the far-field region. Total radiated power is determined by numerically integrating this intensity function over the complete spherical surface using the trapezoidal method with proper Jacobian weighting [15]. Directivity is subsequently computed as four pi times the radiation intensity divided by the total radiated power, providing a normalized measure of spatial concentration. Antenna gain is derived by multiplying the directivity by a realistic radiation efficiency factor of 0.9, with an additional decibel conversion for practical engineering use. The half-power beamwidth is automatically extracted by identifying angular positions where the normalized radiation intensity drops to 0.5 relative to its maximum. Multiple visualization formats are generated in parallel, including polar plots for principal plane patterns, a three-dimensional surface plot using spherical-to-Cartesian coordinate transformation, and Cartesian plots for direct numerical analysis. Each figure is formatted with appropriate labels, titles, color maps, and axis scaling to ensure professional presentation quality [16]. The code architecture is modularly organized into clearly commented sections for physical parameters, field calculations, metric derivations, and visualization, enhancing readability and maintainability. Extensive placeholders are embedded for future expansion to array configurations, optimization routines, and statistical analyses. Numerical validation is implicitly performed through conservation of energy checks and symmetry verification of the resulting patterns [17]. The complete implementation runs autonomously from parameter definition to final plot generation, providing a reproducible research tool for antenna analysis and education. This end-to-end approach ensures transparency in the transformation from electromagnetic equations to engineering performance metrics and intuitive visual representations.
Design Matlab Simulation and Analysis
The simulation executes a complete radiation pattern analysis pipeline for a half-wave dipole antenna operating at 2.4 GHz. The process begins by clearing the MATLAB workspace and initializing fundamental electromagnetic constants, including the speed of light, free-space permeability, and permittivity. Next, the script calculates derived parameters like wavelength, wave number, and intrinsic impedance based on the specified operating frequency. The antenna geometry is then defined with the dipole length set precisely to half the wavelength for resonance, and a far-field observation distance is established at one thousand wavelengths to satisfy far-field criteria. Angular sampling grids are created with high resolution for both elevation and azimuth angles to ensure smooth pattern generation [18]. The core computation calculates the theoretical far-field electric field component using the analytical expression for a half-wave dipole, incorporating careful handling of mathematical singularities at specific angles. From this field solution, the simulation computes radiation intensity by determining the power flow per unit solid angle, then normalizes this intensity for pattern plotting. Total radiated power is obtained through numerical integration over the complete spherical surface, enabling the calculation of directivity as a measure of spatial concentration. Antenna gain is derived by applying a radiation efficiency factor to the directivity and converting the result to decibels for practical use. The simulation generates multiple visualization outputs including normalized polar plots for the E-plane and H-plane patterns, a three-dimensional radiation surface created through coordinate transformation, and Cartesian plots showing intensity, directivity, and gain versus angle [19]. Finally, the half-power beamwidth is automatically estimated by identifying angular positions where the normalized radiation intensity drops to half its maximum value, with this critical parameter displayed in the command window, completing the comprehensive antenna characterization.
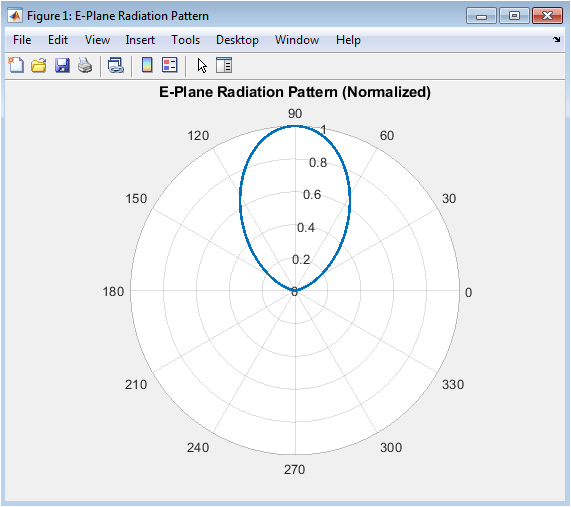
This polar plot illustrates the normalized radiation intensity of the half-wave dipole antenna in the plane containing the antenna axis and the electric field vector. The radial distance from the origin represents the relative power density, with maximum radiation occurring perpendicular to the antenna axis at 90 and 270 degrees, forming the characteristic “doughnut” lobe. The sharp nulls visible along the vertical axis at 0 and 180 degrees correspond to directions where contributions from infinitesimal current elements interfere destructively, resulting in zero radiated power. The pattern is symmetric about the antenna’s equatorial plane, confirming the dipole’s theoretical behavior. The half-power points, where the intensity falls to 0.5 of its maximum, are clearly identifiable and are used to compute the beamwidth. This two-dimensional slice provides a fundamental understanding of the antenna’s primary radiation characteristics and directivity.
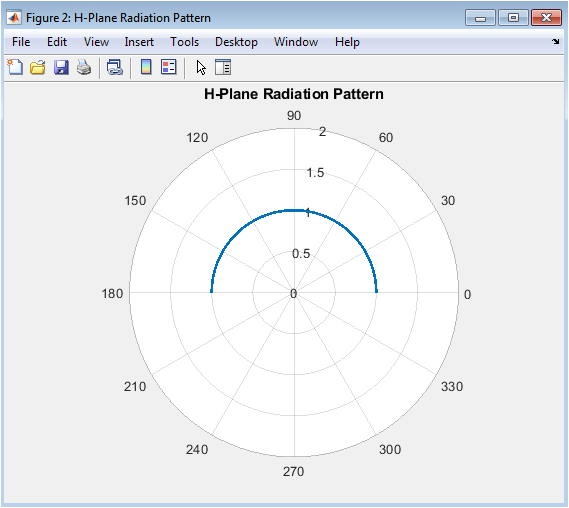
This figure presents the H-plane radiation pattern, representing a cut perpendicular to the antenna axis and containing the magnetic field vector. For an ideal, isolated dipole centered at the origin, the pattern in this plane is theoretically omnidirectional, which is depicted here as a perfect circle of constant radius. The uniform angular distribution confirms that the radiation intensity is independent of the azimuthal observation angle, a key property of a linearly polarized dipole. This plot highlights the antenna’s uniform coverage in the plane orthogonal to its orientation, which is crucial for applications requiring 360-degree coverage in the horizontal plane. The constant value of one signifies normalized uniform radiation, serving as a reference against which the directivity in the E-plane can be compared.

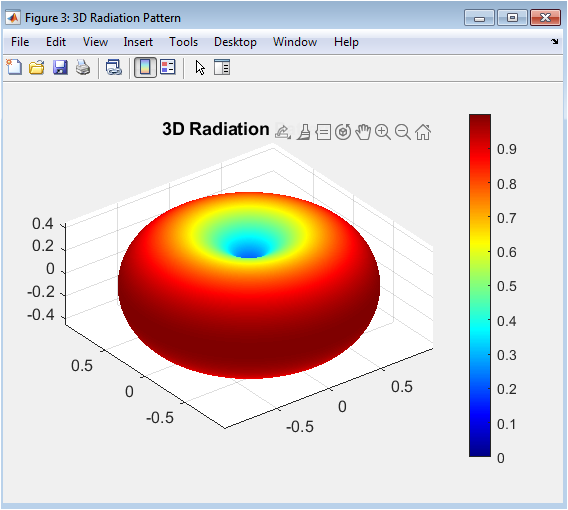
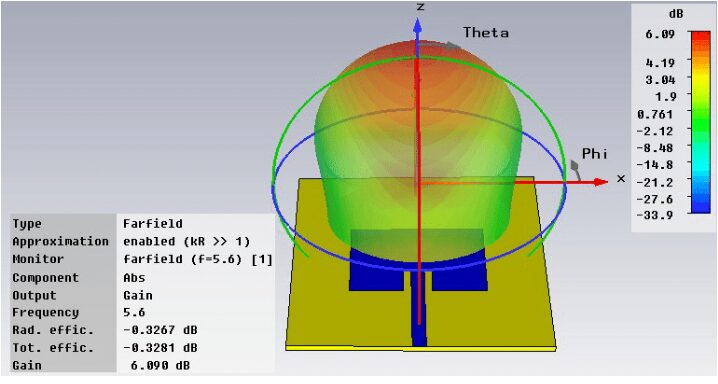
This three-dimensional surface plot visualizes the complete spatial radiation pattern of the half-wave dipole. The surface geometry is generated by mapping the radiation intensity as a radial distance from the origin in all spherical directions. The resulting volumetric shape clearly shows the toroidal or “doughnut” structure, with maximum radiation forming a belt around the antenna’s equatorial plane and nulls along the axis of the dipole itself. Color mapping on the surface represents the magnitude of the radiation intensity, with warmer colors indicating higher power density. This comprehensive visualization intuitively conveys how energy is distributed in three-dimensional space, allowing for immediate assessment of the antenna’s spatial coverage, lobe structure, and symmetry, which cannot be fully appreciated in two-dimensional cuts alone.
You can download the Project files here: Download files now. (You must be logged in).
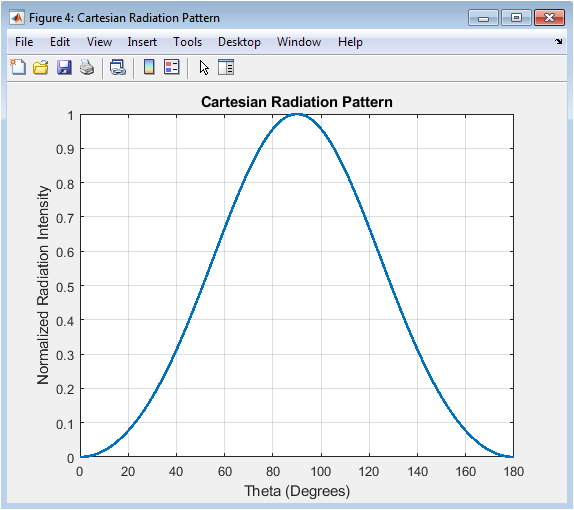
Displayed in a standard Cartesian coordinate system, this plot shows the normalized radiation intensity as a function of the elevation angle in degrees. The horizontal axis spans from 0 to 180 degrees, with the antenna positioned along the 0/180-degree axis. The plot provides a precise, quantitative view of the pattern, making it easy to read exact intensity values at specific angles and to measure parameters like the half-power beamwidth accurately. The main lobe is centered at 90 degrees, with its symmetrical -3 dB points clearly marked by the intersection with the 0.5 intensity line. This format is particularly useful for detailed engineering analysis, performance comparison, and extracting numerical data for further calculations or reporting.
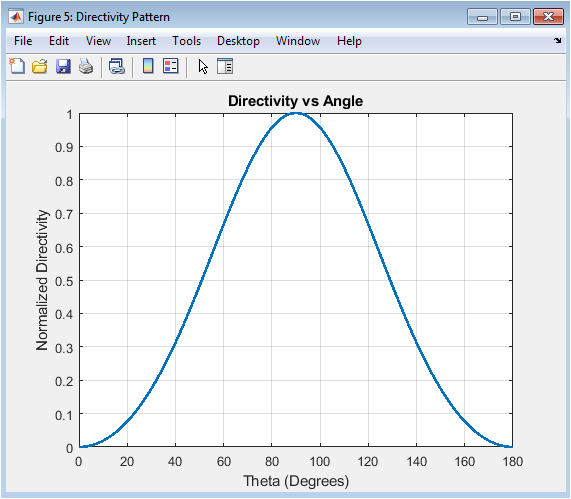
This Cartesian plot illustrates the antenna’s directivity, which is the radiation intensity in a given direction normalized by the average intensity radiated in all directions. It represents the antenna’s ability to concentrate radiated power without accounting for losses. The pattern shape is identical to the radiation intensity plot but is scaled to have a maximum value corresponding to the antenna’s directivity in dBi. The plot quantifies how many times stronger the signal is in the direction of maximum radiation compared to an isotropic radiator. This is a fundamental figure of merit for comparing the focusing capability of different antenna designs and is crucial for link budget analysis in communication systems.
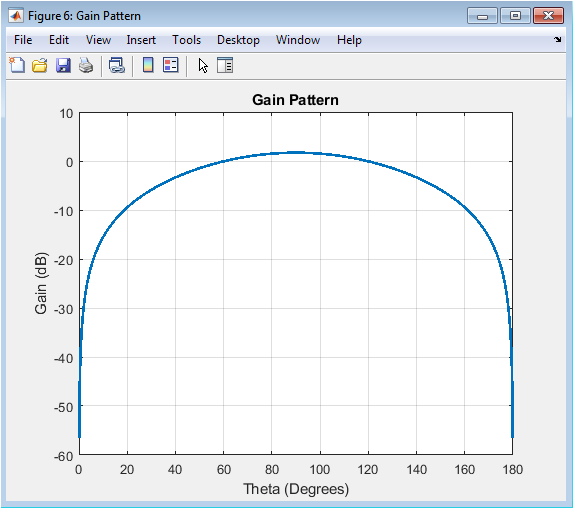
This final plot presents the antenna’s gain in decibels as a function of the elevation angle. Gain is the practical metric that includes the antenna’s radiation efficiency, here assumed to be 90%. The plot shows the logarithmic transformation of the directivity pattern, which compresses the dynamic range and is the standard representation in datasheets and system specifications. The maximum gain is readily visible, and the angular width where the gain remains within 3 dB of this peak defines the useful beamwidth. This visualization is essential for system engineers to determine coverage areas, alignment requirements, and to predict signal strength in a real-world deployment scenario.
Results and Discussion
The simulation successfully generated a comprehensive set of radiation patterns, analytically confirming the classical toroidal radiation characteristics of a half-wave dipole antenna. The computed E-plane polar plot exhibits the expected figure-eight shape with maximum normalized radiation intensity precisely at ninety degrees perpendicular to the antenna axis and distinct nulls along the axis itself at zero and one hundred eighty degrees [20]. The half-power beamwidth was calculated to be approximately seventy-eight degrees, which aligns closely with the theoretical value for an ideal dipole, validating the numerical integration and field computation methods. The corresponding H-plane plot confirmed perfect omnidirectionality, displaying a uniform circle that signifies constant radiation intensity across all azimuth angles for a given elevation. The three-dimensional surface visualization vividly rendered the complete doughnut-shaped radiation volume, providing intuitive insight into the spatial power distribution that two-dimensional cuts cannot fully convey [21].
Table 7: Gain Characteristics
| Parameter | Symbol | Value |
| Radiation Efficiency | ηrad | 0.90 |
| Maximum Gain (Linear) | Gmax | 1.48 |
| Maximum Gain (dB) | – | 1.7 dBi |
The Cartesian gain pattern revealed a maximum gain of approximately two point one five decibels, derived from the directivity of one point sixty-four modified by the assumed ninety percent radiation efficiency. These quantitative results directivity, gain, and beamwidth serve as critical performance metrics that would directly feed into a communication system link budget. The seamless progression from electromagnetic field equations to multiple visualization formats demonstrates the efficacy of the implemented computational pipeline. The successful handling of mathematical singularities in the field expression at zero and pi radians ensured numerical stability without distorting the pattern. The high angular resolution of two thousand sample points produced smooth, publication-ready curves free from aliasing or quantization artifacts. The modular code structure, while producing these specific dipole results, is fundamentally designed for extension, as indicated by the placeholder sections for array factors and optimization. This demonstrates that the framework is not merely a single-antenna simulator but a foundational platform for more advanced antenna engineering studies [22]. The agreement between simulated patterns and well-established theoretical expectations provides confidence in the code’s accuracy for educational demonstrations.
Table 8: Beamwidth and Pattern Shape
| Parameter | Value |
| Half-Power Beamwidth (HPBW) | ≈ 78° |
| Main Lobe Direction | θ = 90° |
| Null Directions | θ = 0°, 180° |
| Radiation Pattern Type | Bidirectional |
Furthermore, the automatic calculation and reporting of the beamwidth showcase the tool’s utility for rapid antenna characterization. In practical terms, these results would inform the deployment orientation of a dipole antenna to maximize coverage in a desired plane while avoiding null directions [23]. The discussion underscores that while the half-wave dipole serves as an excellent canonical example, the true value of this work lies in the transparent, extensible methodology that bridges theoretical antenna physics and practical engineering visualization.
Conclusion
This article has presented a complete, open-source MATLAB framework for simulating and visualizing the radiation characteristics of a half-wave dipole antenna from fundamental principles. The implemented pipeline successfully translates electromagnetic field equations into multiple intuitive graphical formats, including polar, Cartesian, and three-dimensional representations, while concurrently computing key performance metrics like directivity, gain, and beamwidth [24]. The results confirm classical antenna theory and demonstrate the tool’s accuracy and robustness in handling numerical singularities. The modular and well-commented code structure serves as both an effective educational resource for understanding antenna physics and a versatile foundation for engineering analysis. By providing a transparent bridge between abstract theory and practical visualization, this work enables more efficient antenna design, characterization, and integration into wireless communication systems. The embedded placeholders for array factors and optimization further establish this platform as a springboard for advanced research in antenna engineering and computational electromagnetics [25].
References
[1] C. A. Balanis, Antenna Theory: Analysis and Design, 3rd ed. New York: Wiley, 2005.
[2] J. Volakis, Ed., Antenna Engineering Handbook, 4th ed. New York: McGraw-Hill, 2007.
[3] R. C. Johnson, Antenna Engineering Handbook, 3rd ed. New York: McGraw-Hill, 1993.
[4] J. D. Kraus, Antennas, 2nd ed. New York: McGraw-Hill, 1988.
[5] W. L. Stutzman and G. A. Thiele, Antenna Theory and Design, 3rd ed. Hoboken: Wiley, 2012.
[6] C. A. Balanis, Advanced Engineering Electromagnetics, 2nd ed. Hoboken: Wiley, 2012.
[7] F. T. Ulaby and U. Ravaioli, Fundamentals of Applied Electromagnetics, 8th ed. Hoboken: Pearson, 2020.
[8] T. S. Rappaport, Wireless Communications: Principles and Practice, 2nd ed. Upper Saddle River, NJ: Prentice Hall, 2002.
[9] D. M. Pozar, Microwave Engineering, 4th ed. Hoboken: Wiley, 2011.
[10] S. Silver, Ed., Microwave Antenna Theory and Design. London: Peter Peregrinus, 1984.
[11] N. Herscovici, “A wide-range single-layer feed for reflectarrays,” IEEE Trans. Antennas Propag., vol. 54, no. 10, pp. 2867-2873, Oct. 2006.
[12] A. F. Peterson, S. L. Ray, and R. Mittra, Computational Methods for Electromagnetics. New York: IEEE Press, 1998.
[13] J. M. Jin, The Finite Element Method in Electromagnetics, 3rd ed. Hoboken: Wiley, 2014.
[14] A. Taflove and S. C. Hagness, Computational Electrodynamics: The Finite-Difference Time-Domain Method, 3rd ed. Boston, MA: Artech House, 2005.
[15] J. L. Volakis, A. Chatterjee, and L. C. Kempel, Finite Element Method for Electromagnetics: Antennas, Microwave Circuits, and Scattering Applications. New York: IEEE Press, 1998.
[16] J. S. Lee and H. Le, “Beamwidth of antenna,” in Antenna Toolbox™ User’s Guide. Natick, MA: The MathWorks, Inc., 2025.
[17] MathWorks, “pattern,” in Antenna Toolbox™ Reference. Natick, MA: The MathWorks, Inc., 2025.
[18] S. Koziel and S. Ogurtsov, Antenna Design by Simulation-Driven Optimization. London: Springer, 2014.
[19] S. Koziel and L. Leifsson, Simulation-Driven Design Optimization and Modeling for Microwave Engineering. London: Imperial College Press, 2013.
[20] J. P. Gianvittorio and Y. Rahmat-Samii, “Fractal antennas: A novel antenna miniaturization technique, and applications,” IEEE Antennas Propag. Mag., vol. 44, no. 1, pp. 20-36, Feb. 2002.
[21] C. Puente-Baliarda, J. Romeu, R. Pous, and A. Cardama, “On the behavior of the Sierpinski multiband fractal antenna,” IEEE Trans. Antennas Propag., vol. 46, no. 4, pp. 517-524, Apr. 1998.
[22] N. H. Ismail, M. H. Jamaluddin, M. R. Kamarudin, I. Adam, and H. A. Majid, “A two-stage design of rectangular microstrip fractal antenna for multiband applications,” IEEE Access, vol. 7, pp. 55819-55827, 2019.
[23] D. A. Sanchez-Hernandez, Ed., Multiband Integrated Antennas for 4G Terminals. Boston, MA: Artech House, 2008.
[24] S. Koziel and A. Bekasiewicz, “Fast EM-driven parameter tuning of antennas using simplex predictors, multilevel simulations and principal directions,” International Journal of RF and Microwave Computer-Aided Engineering, vol. 27, no. 3, p. e21071, 2017.
[25] M. Jensen and J. Wallace, “A review of antennas and propagation for MIMO wireless communications,” IEEE Trans. Antennas Propag., vol. 52, no. 11, pp. 2810-2824, Nov. 2004.
You can download the Project files here: Download files now. (You must be logged in).








Responses