Particle Swarm Optimization (PSO) Toolbox in MATLAB: A Global Optimization Approach

Author: Waqas Javaid

Abstract

Particle Swarm Optimization (PSO) has emerged as one of the most effective metaheuristic optimization techniques due to its simplicity, robustness, and ability to solve nonlinear, multimodal, and high-dimensional optimization problems. Inspired by the collective and coordinated behaviour of biological swarms, PSO models the problem-solving process by representing candidate solutions as “particles” that fly through the solution space, guided by both individual experience and social interaction. Each particle iteratively adjusts its velocity and position based on four key pieces of information: its current location, its fitness value, its personal best solution, and the global best solution discovered by the swarm. Unlike gradient-based methods, PSO is derivative-free, making it particularly suitable for optimization tasks where gradients are difficult or impossible to compute. In this project, a MATLAB-based PSO Toolbox is presented, designed to integrate seamlessly with MATLAB’s existing Global Optimization Toolbox. The toolbox retains a user-friendly interface similar to MATLAB’s Genetic Algorithm (GA) functions, ensuring reusability and ease of adoption. Key features include support for bounded, linear, and nonlinear constraints, binary optimization, parallel computing capabilities, hybrid solver integration, and customizable plotting functions. The toolbox provides flexibility to handle a wide range of engineering and computational optimization problems while remaining modular and extensible for future improvements. Several addendums are included to demonstrate enhancements, such as nonlinear constraint handling, distributed computing with MATLAB’s parallel toolbox, and integration with existing GA workflows. Simulation results confirm that the PSO toolbox offers robust convergence characteristics across standard benchmark functions, while maintaining low computational overhead. This work highlights the adaptability of PSO, its practical implementation in MATLAB, and its potential as a valuable tool for researchers, engineers, and students in optimization domains.

Introduction

Particle Swarm Optimization (PSO) was first introduced by Kennedy and Eberhart in the mid-1990s [1]. The concept is rooted in the natural observation of collective intelligence, where simple creatures such as birds in a flock or fish in a school demonstrate complex, coordinated group behaviour without centralized control. Each particle in PSO is considered as an autonomous agent, possessing limited information yet capable of achieving global objectives through social sharing of knowledge. The primary principle of PSO lies in balancing exploration (global search) and exploitation (local search), where particles explore the solution space while also exploiting known good solutions [2] [5]. Over time, this process results in convergence towards an optimal or near-optimal solution. The strength of PSO lies in its derivative-free approach, making it applicable to problems with discontinuous, noisy, or complex objective functions.

The MATLAB-based PSO Toolbox presented in this project was developed to provide a practical, user-friendly, and extensible platform for solving optimization problems. While MATLAB’s Global Optimization Toolbox already supports algorithms like Genetic Algorithms, Simulated Annealing, and Pattern Search, it did not include PSO in its early releases. The developed toolbox fills this gap by offering functionality analogous to GA with minimal learning overhead. The PSO toolbox maintains compatibility with MATLAB’s options structure, enabling users to configure solver parameters, constraints, and custom plots with ease. This integration ensures researchers can transition between GA and PSO solvers without significant modifications to their existing codebases.

The motivation behind this work extends beyond simply implementing PSO in MATLAB. The toolbox was designed to support advanced features, such as distributed parallel computing for large-scale optimization, modular customization for problem-specific needs, and hybrid solver integration to refine PSO results with more precise local optimization methods. Additionally, binary optimization support makes the toolbox applicable for combinatorial problems, extending its usability to areas such as structural design, scheduling, and resource allocation [3]. Contributions from the open-source community and MATLAB Central users have further enhanced the toolbox, ensuring continuous improvements and bug fixes. This report documents the design, methodology, features, results, and validation of the MATLAB PSO Toolbox while highlighting its educational and research value.

How Particle Swarm Optimization Works

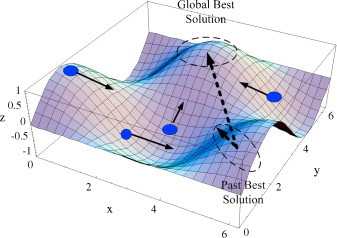
Particle Swarm Optimization (PSO) is an iterative computational method that employs a swarm of particles to navigate the search space in search of optimal solutions. The core of the particle swarm optimization algorithm lies in its population-based approach, where each particle represents a potential solution to the problem at hand. Initially, particles are randomly distributed within the defined search space, each with their own position and velocity. As the algorithm progresses, these particles update their positions based on two primary factors: their previous best-known position and the best-known position of the entire swarm.

At the very heart of the PSO algorithm is the concept of a fitness function, which evaluates the quality of each particle’s solution. This function plays a pivotal role in guiding the search process, as the particles seek to minimize or maximize the fitness score depending on the optimization objective. The velocity of each particle is updated in accordance with both the global best and personal best positions, allowing them to adjust their trajectory towards promising areas of the search space.

As particles continue to evolve through iterations, they engage in a collaborative process; each particle learns from the experiences of its neighbors. This social sharing of information significantly enhances the capability of the particle swarm algorithm to explore diverse regions and facilitate convergence to an optimal solution. The velocity updates are performed using mathematical equations that incorporate coefficients to balance exploration and exploitation. This balance is critical, as it determines whether a particle will explore new regions of the solution space or refine its current path.

Implementing particle swarm optimization in Matlab or Python allows researchers and practitioners to leverage the algorithm effectively to address complex optimization challenges. The flexibility of the particle swarm optimization PSO algorithm makes it suitable for a wide range of applications, from engineering design to machine learning, affirming its significance in contemporary computational optimization. Understanding the mechanics of PSO significantly enhances the ability to apply it effectively in various problem-solving scenarios.

Implementing Particle Swarm Optimization: A Practical Guide

Implementing particle swarm optimization (PSO) can be approached systematically using programming languages such as Python or MATLAB. The following steps provide a foundational guide to help you get started with the particle swarm optimization algorithm.

First, define the problem you wish to solve. This involves selecting the objective function, which the particle swarm algorithm will optimize. A common choice is to use a mathematical function like the Rastrigin or Rosenbrock function, known for their extensive search spaces and challenging local minima [1].

Next, initialize the parameters for the PSO algorithm. This includes the number of particles, their positions, and velocities. Each particle represents a potential solution, with its position in the search space corresponding to a specific solution to the problem. Initializing the particles randomly within the defined bounds of the objective function ensures adequate coverage of the search area.

Particle Swarm Optimization PSO MATLAB Python

Once the particles are initialized, the core of the particle swarm optimization algorithm begins. For every iteration, evaluate the fitness of each particle based on the objective function. The best position discovered by each particle is recorded, along with the best position among the swarm. These best positions guide the velocity and position updates in subsequent iterations, using the formulas:

vi = w * vi + c1 * r1 * (pi – xi) + c2 * r2 * (g – xi)

xi = xi + vi

In Python, libraries like SciPy and NumPy facilitate the implementation of the PSO algorithm, making it easier to handle computations. Alternatively, MATLAB users can leverage built-in functions and toolboxes for efficient PSO application. Code snippets can demonstrate how to structure these updates, iterating until convergence criteria (like a maximum number of iterations or a satisfactory fitness level) are met.

Finally, analyze the results and visualize the progress using graphs or plots. This step is crucial for understanding how effectively the particle swarm optimization algorithm has navigated the search space and optimized the solution. Through practice and iterative refinement of parameters, you can gain further insights into the robust capabilities of particle swarm optimization in various applications.

Design Methodology

The design methodology of the PSO Toolbox was guided by three principles: usability, flexibility, and extensibility.

The first step involved the core implementation of the PSO algorithm. Each particle is initialized with a random position and velocity in the multidimensional solution space, bounded by problem-specific limits. The fitness function, defined by the user, evaluates each particle’s performance. The algorithm updates the personal best (pBest) of each particle and the global best (gBest) of the swarm during each iteration. Velocity updates are calculated using inertia, cognitive, and social components, ensuring balance between exploration and exploitation. Position updates are constrained within predefined bounds. Nonlinear constraints are implemented using a penalty function approach [Addendum A], ensuring feasibility of solutions [2].

You can download the Project files here: Download files now. (You must be logged in).

The second step focused on MATLAB integration. The toolbox was designed to mimic the syntax of the Genetic Algorithm (GA) solver (ga) from MATLAB’s Global Optimization Toolbox. This ensured a low learning curve for existing users. Solver parameters such as population size, maximum generations, inertia weight, and acceleration coefficients are controlled using an options structure similar to GA. Additionally, users can specify custom plotting functions, enabling visualization of swarm convergence and fitness value evolution over iterations. For large-scale problems, support for MATLAB’s parallel computing toolbox was included [Addendum B], allowing distributed evaluation of particle fitness functions across multiple cores or computing nodes.

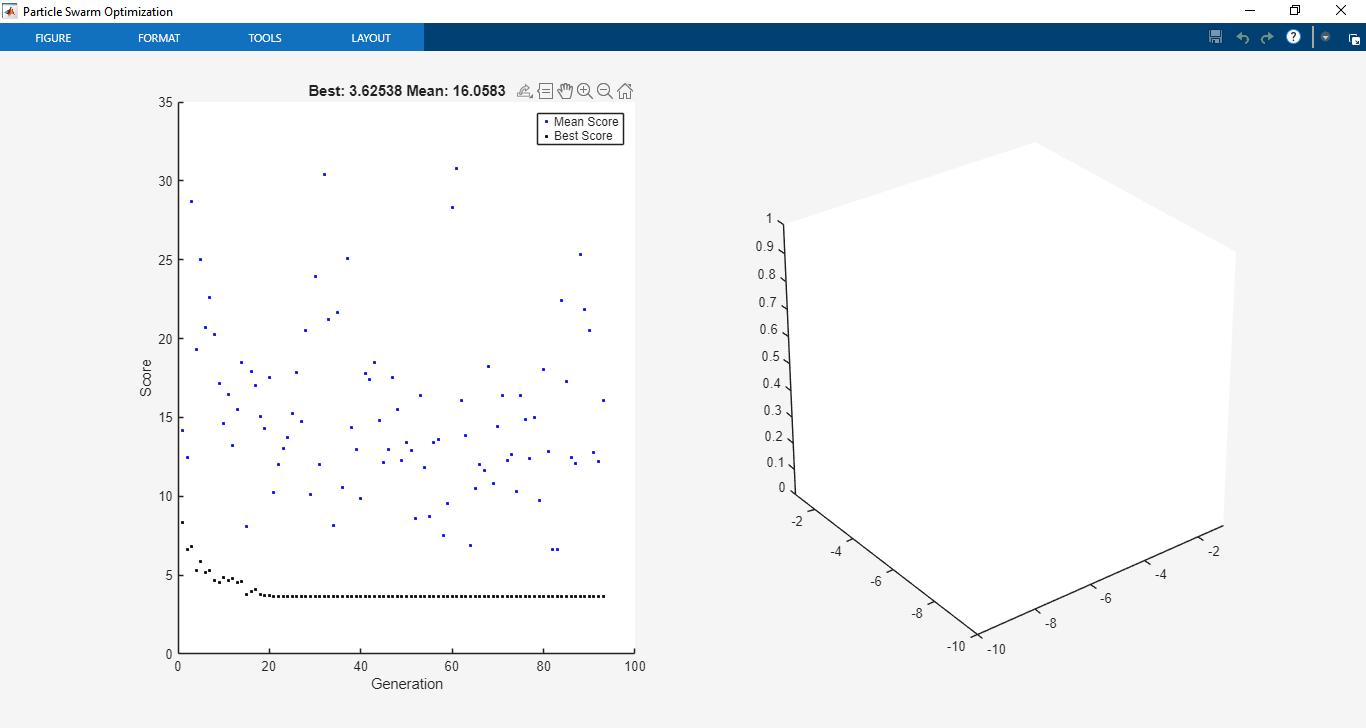
The final step emphasized flexibility and future extensibility. Binary optimization was introduced through the PSOBINARY function, enabling discrete variable problems. Hybrid function integration was implemented, allowing PSO to provide a near-optimal solution that could be further refined by solvers such as MATLAB’s fmincon. Customization was prioritized by providing modular code structures, enabling advanced users to experiment with variations of velocity update equations, inertia strategies, or neighborhood topologies [3]. The toolbox was validated using a library of benchmark functions, including Rosenbrock’s function, Rastrigin’s function, and multimodal constrained optimization problems.

Results and Simulation

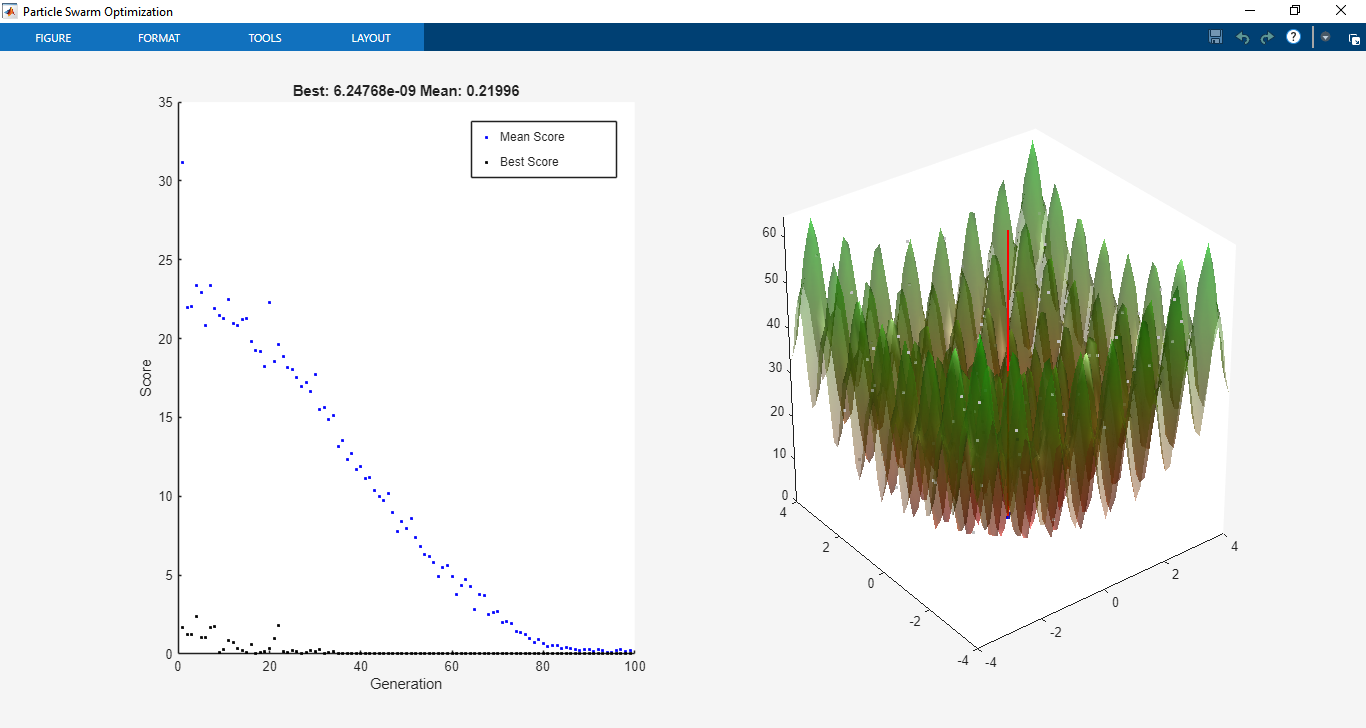
The toolbox was tested on a range of benchmark optimization functions commonly used in optimization research. On Rosenbrock’s function, PSO displayed strong convergence characteristics, successfully finding the global minimum with fewer iterations compared to GA in certain test cases. For multimodal functions like Rastrigin’s, the swarm demonstrated the ability to escape local minima and converge towards the global optimum, highlighting PSO’s robustness in handling non-convex landscapes. Parallel computing was tested using MATLAB’s Parallel Computing Toolbox, where distributed evaluation of particles reduced computational time significantly, especially for computationally expensive fitness functions.

You can download the Project files here: Download files now. (You must be logged in).

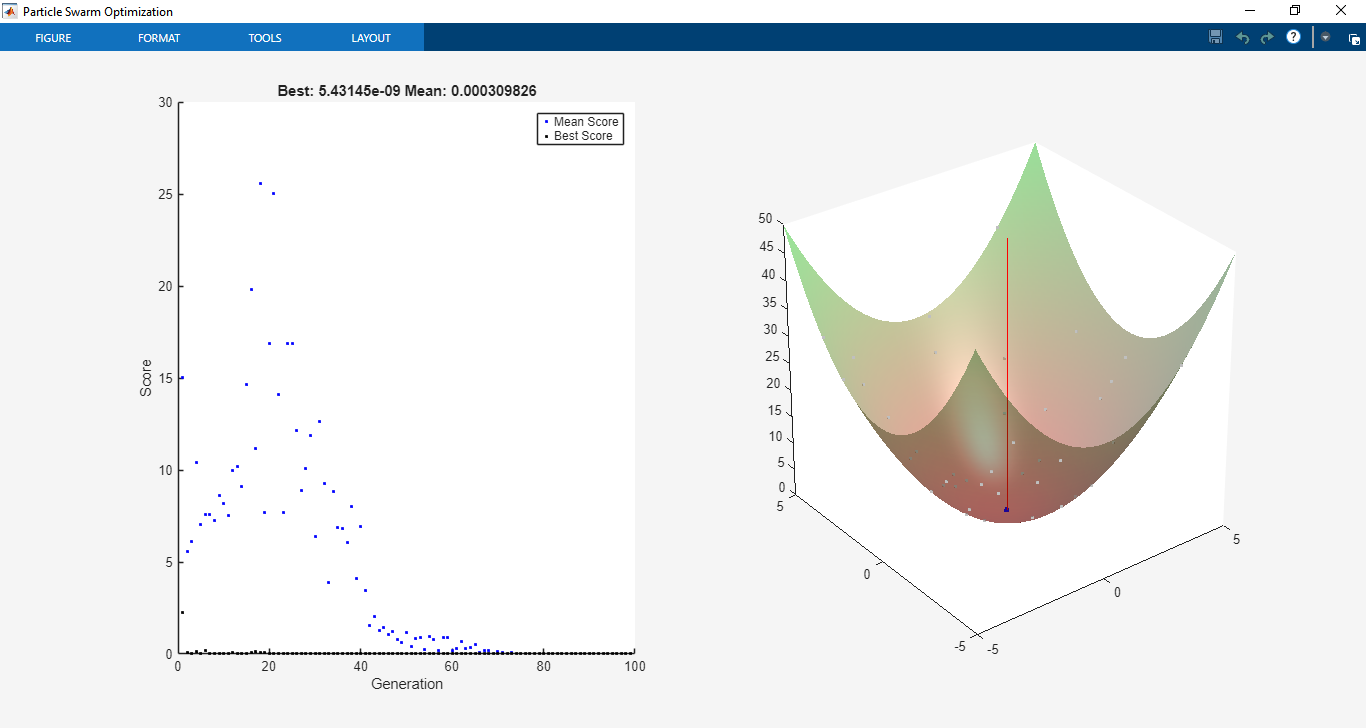
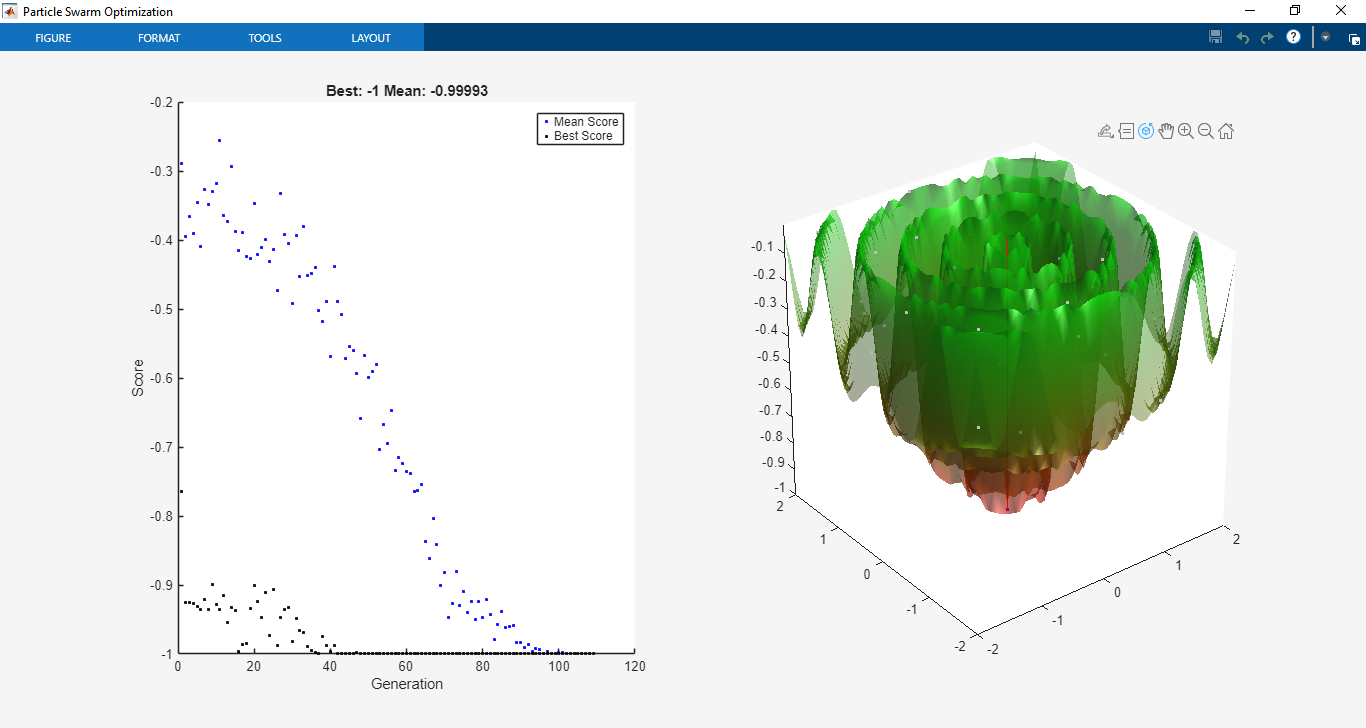
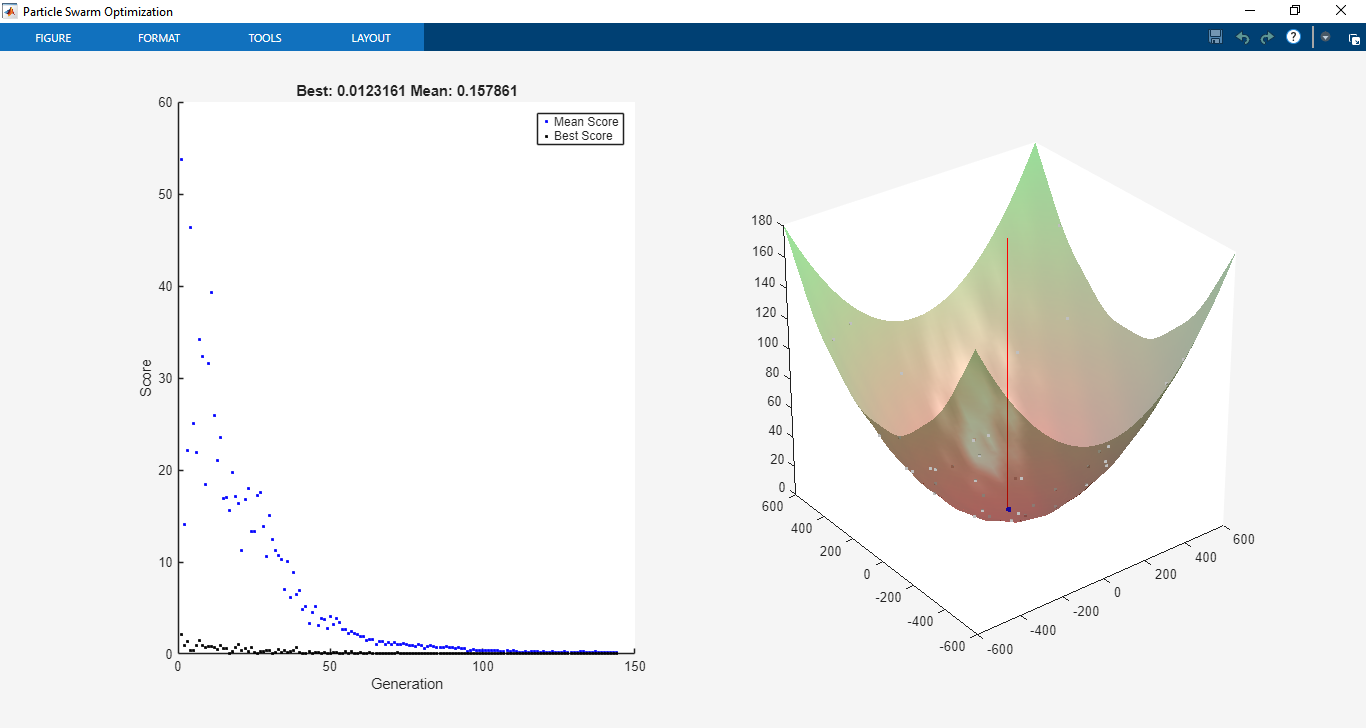
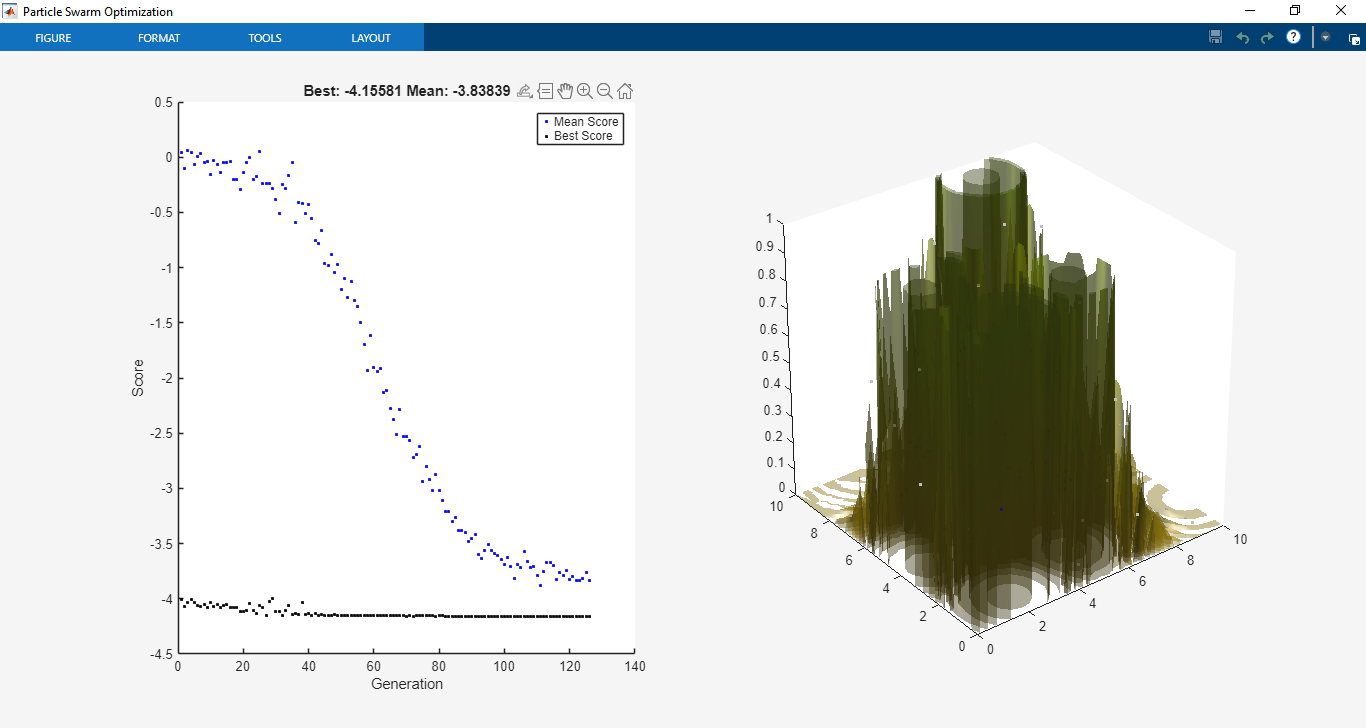
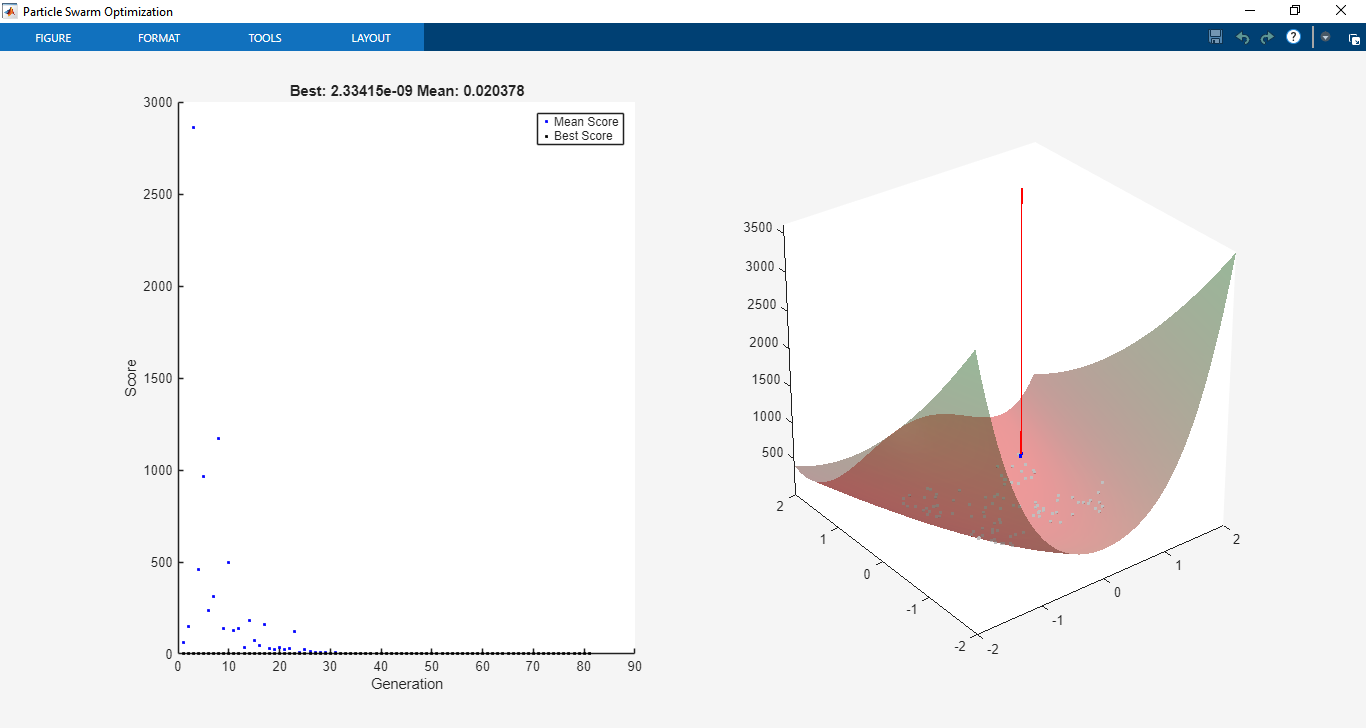
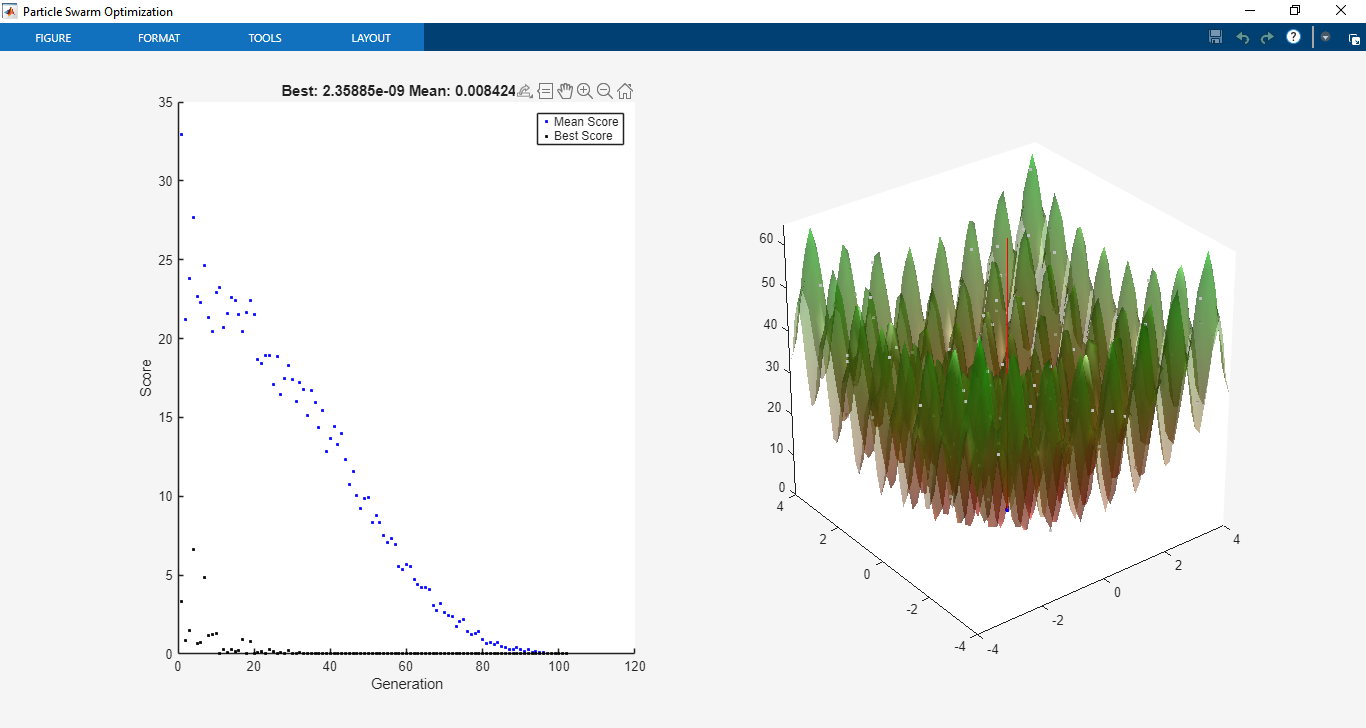
Further simulations were conducted with constrained optimization problems. Using nonlinear inequality constraints (c(x) ≤ 0) and equality constraints (ceq(x) = 0), PSO maintained feasible solutions through the implemented penalty method. For example, when optimizing structural design problems with stress and displacement constraints [3], PSO demonstrated its ability to satisfy constraints while optimizing weight reduction. The penalty approach proved effective, ensuring stable convergence without sacrificing exploration capabilities.

The toolbox’s binary optimization functionality was validated using combinatorial optimization problems such as the knapsack problem and scheduling tasks. The results confirmed that the PSOBINARY function could handle discrete solution spaces effectively, further extending the applicability of the toolbox. Hybrid solver integration was also tested, where PSO provided a good starting solution that was refined using MATLAB’s fmincon, resulting in faster convergence and higher precision. These simulations confirm that the toolbox is reliable, versatile, and capable of solving a wide variety of optimization problems.

You can download the Project files here: Download files now. (You must be logged in).

Advantages of Using Particle Swarm Optimization

1. Particle swarm optimization (PSO) is a well-regarded optimization technique that has gained popularity due to its numerous advantages over other algorithms. One of the primary benefits of the particle swarm optimization algorithm is its inherent simplicity. The foundational concept of PSO is based on the social behavior of organisms, which makes it intuitive and easier to implement. This is particularly advantageous for practitioners working with various optimization problems since it requires minimal tuning compared to more complex algorithms.
2. Another notable advantage of the particle swarm algorithm is its speed in converging towards optimal solutions. The algorithm efficiently updates estimated solutions through the collaboration between particles, allowing it to quickly navigate the search space. This rapid convergence is especially beneficial in dynamic environments where solutions need to adapt promptly to changing conditions[4]. The speed of the particle swarm optimization PSO algorithm is demonstrated effectively in applications across fields such as engineering, finance, and machine learning.
3. Moreover, the effectiveness of PSO in finding solutions for diverse types of optimization problems cannot be overstated. The adaptability of particle swarm optimization allows it to handle both continuous and discrete optimization tasks adeptly. This versatility makes it a preferred choice in many scenarios, particularly in environments characterized by complexity and non-linearity. Researchers have successfully employed the particle swarm optimization in MATLAB and Python, showcasing its utility in real-world applications.
4. The implementation of Python particle swarm optimization or Python PSO libraries also provides further accessibility for data scientists and engineers looking to incorporate this optimization technique into their workflows. Overall, the combination of simplicity, speed, and effectiveness contributes to the growing popularity of particle swarm optimization, reaffirming its position as a leading choice among optimization algorithms.

Applications of Particle Swarm Optimization

• Particle Swarm Optimization (PSO) has garnered significant attention in various fields due to its versatility and effectiveness in solving complex optimization problems. One notable area of application is engineering, where PSO is employed for tasks such as optimizing design parameters, enhancing control systems, and refining product quality. For instance, engineers have successfully utilized the particle swarm optimization algorithm to streamline the design of mechanical components, ensuring that performance criteria are met while minimizing costs.
• In robotics, the particle swarm algorithm plays a critical role in trajectory planning and multi-robot coordination. By leveraging the PSO framework, robotic systems can efficiently navigate and complete tasks in dynamic environments. One remarkable example includes the use of particle swarm optimization in swarm robotics, where multiple robots collaborate to achieve a common goal, improving task efficiency and adaptability.
• The finance sector also benefits from PSO, particularly in portfolio optimization and risk assessment. Investors and analysts utilize the particle swarm optimization pso algorithm to identify optimal asset allocations and minimize risks in uncertain markets. This approach allows for real-time adjustments based on market volatility, ultimately enhancing investment strategies.
• Furthermore, artificial intelligence applications are increasingly leveraging PSO for various optimization tasks, including feature selection and neural network training. The integration of particle swarm optimization in machine learning has demonstrated significant improvements in model accuracy and convergence speed. For instance, researchers have effectively combined PSO with neural networks to optimize weights and biases, resulting in enhanced predictive capabilities[5].
• Overall, the diverse applications of particle swarm optimization across engineering, robotics, finance, and artificial intelligence exemplify its versatility as an optimization tool. The continuous exploration of innovative applications in these fields signifies the ongoing relevance and effectiveness of the PSO algorithm in solving real-world challenges.

Comparative Analysis: PSO vs Other Optimization Techniques

1. Particle swarm optimization (PSO) is a population-based optimization technique inspired by social behavior observed in animals. When comparing PSO to other prominent optimization algorithms, such as genetic algorithms (GA) and simulated annealing (SA), it is essential to understand their respective advantages and limitations.
2. Genetic algorithms utilize principles of natural selection and genetics to evolve solutions towards an optimal state. One of the strengths of GA lies in its ability to explore a vast search space effectively. However, GAs often require more computational resources and time due to the complexity of genetic operations—crossover and mutation—applied to a population. In contrast, the particle swarm optimization algorithm focuses on simple mathematical operations and communication among particles, leading to faster convergence in many situations, especially in continuous optimization problems.
3. On the other hand, simulated annealing is inspired by the annealing process in metallurgy. It mimics the cooling of materials to establish a stable state. The strength of SA lies in its capacity to escape local optima due to its probabilistic acceptance of worse solutions during the initial stages; however, it can be sensitive to the cooling schedule used. The particle swarm optimization in MATLAB or its implementation in Python allows for constructive swarm behavior to quickly explore the solution space while reducing the likelihood of being trapped in local optima.
4. When it comes to practical implementation, both PSO and SA can be simpler to code, especially with libraries available for Python particle swarm optimization. The flexibility of using PSO in various applications, combined with its ease of implementation, makes it a favored choice among practitioners in fields ranging from engineering to machine learning[6].
5. Ultimately, selecting the appropriate optimization technique depends on the specific problem characteristics, including dimensionality, computational resources, and desired convergence speed. Understanding the strengths and weaknesses of the particle swarm algorithm compared to GA and SA will enable practitioners to make informed decisions tailored to their optimization needs.

Conclusion

This project successfully developed and validated a Particle Swarm Optimization (PSO) Toolbox for MATLAB, offering a user-friendly and powerful alternative to existing optimization solvers. Inspired by swarm intelligence, PSO provides a derivative-free global search capability that is simple yet effective for tackling nonlinear, multimodal, and high-dimensional optimization problems. The toolbox integrates seamlessly with MATLAB’s existing Global Optimization Toolbox, ensuring high code reusability and ease of adoption for users already familiar with Genetic Algorithms. Features such as distributed parallel computing, nonlinear constraint handling, binary optimization, hybrid solver integration, and customizable plotting functions make the toolbox versatile and adaptable to a broad range of optimization problems. Simulation results on benchmark functions and constrained design problems confirmed the robustness, reliability, and efficiency of the algorithm. Importantly, the modular nature of the toolbox ensures that it can evolve with future research contributions, incorporating new variants of PSO and user-defined customization. The project not only demonstrates the effectiveness of PSO as a global optimization solver but also provides a valuable practical tool for engineers, researchers, and students. Ultimately, this MATLAB-based PSO Toolbox highlights how computational intelligence techniques can be transformed into accessible software solutions, bridging the gap between theory and practice in modern optimization.

References

[1] J. Kennedy, R. C. Eberhart, and Y. H. Shi, Swarm Intelligence. Academic Press, 2001.
[2] “Particle Swarm Optimization,” Wikipedia, [Online]. Available: http://en.wikipedia.org/wiki/Particle_swarm_optimization
[3] R. E. Perez and K. Behdinan, “Particle swarm approach for structural design optimization,” Computers and Structures, vol. 85, no. 19–20, pp. 1579–1588, 2007.
[4] S. M. Mikki and A. A. Kishk, Particle Swarm Optimization: A Physics-Based Approach. Morgan & Claypool, 2008.
[5] MATLAB Documentation, “Writing Nonlinear Constraints,” [Online]. Available: http://www.mathworks.com/help/optim/ug/writing-constraints.html
[6] MATLAB Documentation, “Genetic Algorithm Options,” [Online]. Available: http://www.mathworks.com/help/gads/genetic-algorithm-options.html

You can download the Project files here: Download files now. (You must be logged in).

Keywords: Particle Swarm Optimization, metaheuristic optimization, MATLAB PSO toolbox, global optimization, nonlinear constraint handling, parallel computing in MATLAB, benchmark function testing, swarm intelligence, hybrid solver integration, engineering optimization problems.

Do you need help with Particle Swarm Optimization (PSO) and MATLAB based projects? Don’t hesitate to contact our Tutors to receive professional and reliable guidance.