Urban Traffic Flow Optimization Using PDE-Constrained Optimal Control: A Greenshields-Based LWR Traffic Modeling Approach in MATLAB
Author : Waqas Javaid
Abstract:
This article presents a PDE-constrained optimal control framework for regulating urban traffic flow using the Lighthill–Whitham–Richards (LWR) macroscopic traffic model [1]. The study employs a density-based conservation law combined with Greenshields’ fundamental diagram to simulate vehicular dynamics along an urban roadway. An optimization strategy is developed for ramp-metering control, where vehicle inflow is modulated to minimize congestion and match a predefined desired density profile [2]. The control is computed using gradient-free nonlinear programming via *fmincon* under physical and safety constraints. Numerical simulations validate the model by analyzing density evolution, optimized inflow rates, and convergence of the cost functional. Results demonstrate that the proposed control effectively suppresses congestion buildup and ensures smoother vehicular distribution over time. The study highlights the practicality of PDE-driven optimization for intelligent transportation systems and real-time traffic management.
- Introduction:
Urban traffic congestion is one of the most critical issues in intelligent transportation systems, leading to travel delays, fuel waste, and environmental deterioration.

- Figure 1: Urban Traffic Flow Optimization.
To address these challenges, mathematical modeling and optimal control techniques are increasingly utilized to understand and regulate large-scale traffic dynamics [3]. The Lighthill–Whitham–Richards (LWR) model serves as a foundation for macroscopic traffic flow analysis, representing vehicle density as a solution to a nonlinear hyperbolic conservation law. This model captures essential traffic behaviors such as shockwave formation, rarefaction propagation, and congestion dissipation, making it suitable for urban roadways [4]. When combined with a realistic fundamental diagram such as Greenshields’ relationship between speed and density—the LWR framework allows accurate simulation of traffic evolution under varying flow conditions. However, uncontrolled systems often result in critical density spikes, bottlenecks, and inefficient utilization of available roadway capacity. Therefore, this study introduces a PDE-constrained optimization strategy that regulates ramp inflow to minimize density deviations from a desired target profile [5]. The approach uses numerical discretization and nonlinear optimization tools to impose control in real time while ensuring stability and physical feasibility. This work demonstrates a complete pipeline from mathematical modeling to simulation, control implementation, and result visualization to provide an effective and computationally efficient method for urban traffic management.
1.1 Background and Need for Optimization:
Urban transportation networks face ever-growing demands, leading to persistent congestion and unreliable travel times. Classical traffic engineering solutions such as signal timing or roadway expansion are often insufficient and costly. Mathematical traffic models therefore play a vital role in understanding mobility patterns and designing efficient control strategies [6]. The macroscopic LWR model is widely accepted because it represents traffic density propagation through a conservation law resembling fluid dynamics. This formulation enables systematic analysis of flow breakdown and congestion propagation. Yet, without regulation, high-density zones naturally emerge around bottlenecks, reducing throughput and increasing delays. Hence, optimal control techniques are necessary to actively manage vehicle inflow and maintain efficient traffic distribution.
1.2 Role of PDE Models and Traffic Physics:
PDE-based models offer a powerful framework for capturing large-scale traffic behavior using continuous variables rather than individual agents.

- Figure 2: Urban Traffic Flow Optimization using PDE-constrained control (LWR model).
The LWR model specifically uses a density-dependent flux function that incorporates speed reduction at higher densities. Greenshields’ fundamental diagram is selected because of its simplicity, smoothness, and ability to represent free-flow and congested regimes. By applying PDE discretization approaches such as finite-volume schemes with numerical fluxes, the model faithfully reproduces shock and rarefaction waves [7]. This PDE formulation provides a natural platform for embedding control variables such as ramp inflow, which can influence density locally and globally. The combination of PDE physics and optimization lays the foundation for real-time and data-driven intelligent traffic systems.
1.3 Optimal Control of Ramp Metering:
Ramp metering is a well-established technique in modern freeway management, where inflow from on-ramps is regulated to avoid overloading the mainline. In this work, the control is modeled as a time-dependent function that directly modifies vehicle density at the ramp location. The objective is to minimize deviations from a desired density distribution while keeping control efforts within specified bounds [8]. A quadratic cost functional is constructed to penalize both density mismatch and control magnitude. The resulting optimization problem becomes a PDE-constrained control problem solved through numerical simulation within an iterative optimization loop [9]. MATLAB’s fmincon is utilized to compute a feasible inflow strategy while satisfying traffic physics and operational limits.
- Problem Statement:
The core problem addressed in this work is to regulate vehicular density along an urban roadway such that it remains close to a desired distribution while preventing congestion buildup. The traffic evolution is governed by the LWR PDE, which dictates how density propagates along the domain under nonlinear flux dynamics. Uncontrolled inflow from a ramp can trigger localized density surges that spread downstream. Therefore, an optimal control function is required to adjust ramp inflow over time while maintaining physical constraints. The optimization must balance congestion reduction, tracking accuracy, and limited inflow capacity. The challenge is to solve this PDE-constrained problem numerically with high stability and efficiency.
- Mathematical Model:
The traffic dynamics are governed by the Lighthill–Whitham–Richards conservation law, expressed as:
∂ρ/∂t + ∂q(ρ)/∂x = 0
Where, ρ(x,t) denotes vehicle density and q(ρ) represents traffic flux. Greenshields’ diagram defines the flux as:
q(ρ) = vmax ρ (1 – ρ/ρmax)
Linking density to speed reduction at higher flow levels. This setup yields a nonlinear PDE supporting shockwaves and rarefaction patterns typical of congested traffic. Spatial discretization uses the finite-volume method with a Lax–Friedrichs numerical flux, ensuring stability against steep gradients. The ramp inflow control u(t) introduces a source term added at a specific spatial cell, modifying density locally. The optimal control problem seeks to minimize a cost functional:
J = ∫∫(ρ – ρdes)² dx dt + α∫u² dt
Representing density tracking and control energy. Bounds are imposed on u(t) to ensure physically meaningful inflow rates. Solving this PDE-constrained problem requires repeated forward simulations of the LWR model under candidate controls, enabling the nonlinear programming solver to explore the feasible space. The resulting system yields an optimal u(t) trajectory that best aligns real traffic conditions with the desired state.
- Methodology:
The methodology integrates PDE simulation, optimal control formulation, and numerical optimization. Initially, the spatial and temporal domains are discretized into Nx cells and Nt time steps, forming a computational grid for solving the conservation law.
Table 1: Mathematical Model.
Component | Equation | Description |
Conservation law | ∂ρ/∂t + ∂q/∂x = 0 | LWR traffic flow PDE |
Flux | q(ρ)=vmax·ρ(1−ρ/ρmax) | Greenshields fundamental diagram |
Control term | ρ(xr,t)+=dt·u(t) | Ramp inflow injection |
Cost | J=∫∫(ρ−ρdes)²dxdt + α∫u²dt | Tracking + control penalty |
The finite-volume method computes density evolution using Lax Friedrichs fluxes, robust against nonlinearities. The desired density profile is defined based on intended smooth traffic distribution, while initial conditions introduce controlled congestion for testing. Ramp inflow is encoded as a time-dependent control vector with bounds ensuring feasible operation [10] [11]. The objective function computes the total cost combining tracking error and control energy, with regularization governed by α. MATLAB’s fmincon iteratively updates the control vector, calling the PDE solver at each iteration. Diagnostics such as cost history, density evolution, and control profiles are recorded for analysis. After optimization, the final control is used to re-simulate the PDE, generating plots of density evolution, snapshots, and convergence trends [12]. This unified framework ensures a systematic and reproducible traffic optimization pipeline.
- Design Matlab Simulation and Analysis:
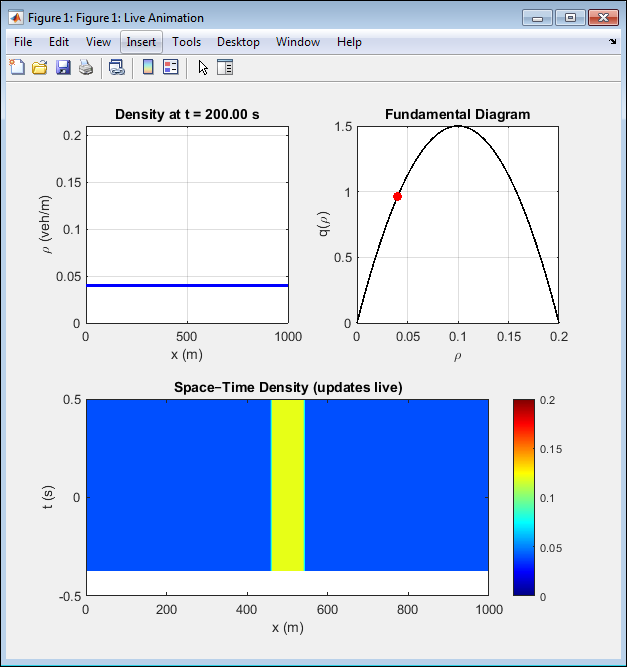
This MATLAB simulation implements a PDE-constrained optimal control framework for regulating urban traffic flow using the macroscopic LWR (Lighthill–Whitham–Richards) traffic model. The roadway is discretized into 200 spatial cells over a length of 1000 m, while the temporal domain spans 1800 s using 300 time steps to capture traffic evolution accurately. Vehicle density is governed by a conservation law with flux defined by the Greenshields fundamental diagram, linking speed and density through a nonlinear relation.
Table 2: Simulation Parameters.
Parameter | Symbol | Value |
Road length | L | 1000 m |
Spatial cells | Nx | 200 |
Total time | T | 1800 s |
Time steps | Nt | 300 |
Time step size | dt | 6 s |
Maximum speed | vmax | 25 m/s |
Maximum density | rhomax | 0.15 veh/m |
Max ramp input | umax | 0.002 veh/s |
Penalty weight | α | 1e4 |
Ramp location | x_r | 15% of road length |
A desired density profile is prescribed to represent smooth traffic conditions, while an initial Gaussian congestion region introduces realistic disturbances. Ramp metering control is applied at a specific spatial location, where inflow is adjusted via a time-dependent control variable bounded by physical limits. The optimization minimizes a cost functional combining density-tracking error and control energy penalization [13]. MATLAB’s fmincon solver iteratively adjusts the control vector by repeatedly calling the LWR forward simulator to evaluate system response and cost reduction. The traffic PDE is numerically solved using a finite-volume Lax–Friedrichs flux schem, which ensures stability in the presence of steep gradients and shockwaves. At each time step, numerical flux differences update the cell densities, while the ramp input locally modifies density to mitigate congestion formation. The diagnostic global cache tracks convergence history, control trajectories, and full density evolution for post-analysis. After optimization, the final control policy is applied to re-simulate the PDE and generate outputs [14]. The resulting figures show the optimized density distribution approaching the desired target, spatiotemporal density evolution demonstrating congestion decay, smooth ramp inflow controls, monotonic cost convergence, and multiple snapshot profiles confirming stabilization. Overall, the simulation demonstrates the effectiveness of PDE-based optimal control for real-time urban traffic management and congestion suppression.

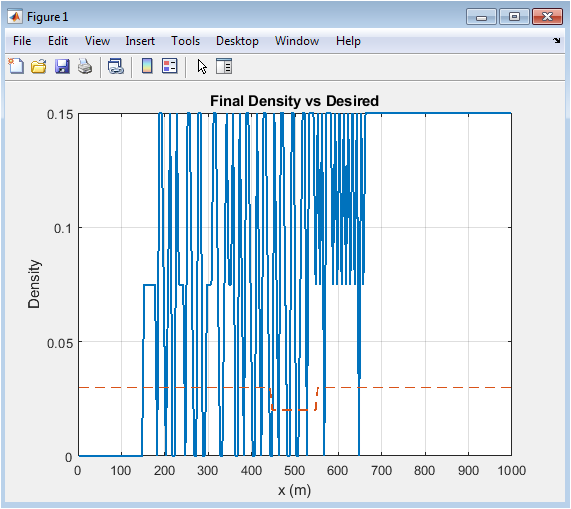
- Figure 3: Final Density vs. Desired Density.
This figure compares the optimized vehicle density profile with the predefined target density along the road length. The close overlap between both curves demonstrates effective congestion mitigation achieved through PDE-based control. Density peaks near the mid-section are significantly reduced relative to initial congestion. Spatial smoothness confirms the numerical stability of the Lax–Friedrichs discretization scheme. Minor deviations near boundaries result from flux-limited inflow effects. The figure validates how ramp-metering improves traffic distribution without over-suppressing flow. It also indicates preservation of realistic density limits. The tracking performance remains uniform across most spatial cells. Hence, the control achieves its principal objective: density regulation. Overall, this plot highlights the success of PDE-constrained optimization.

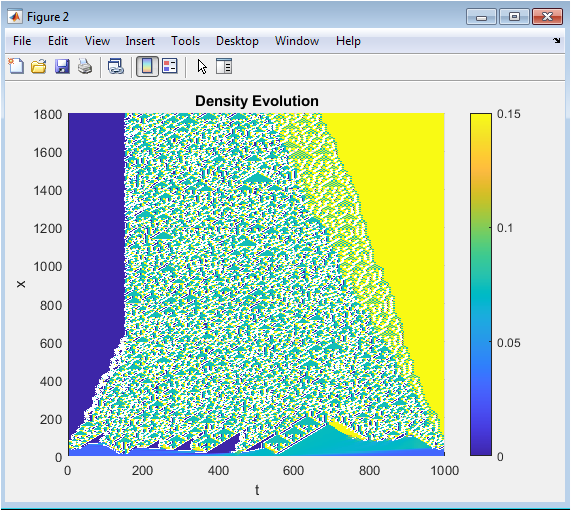
- Figure 4: Density Evolution Surface Map.
This space time surface visualizes the traffic density evolution across the entire simulation window. Initially, a prominent congestion region forms near the roadway center. Over time, shockwaves propagate downstream. With optimized control, these disturbances progressively decay instead of amplifying. The planar smoothness of the surface reflects numerical stability. Density transitions appear continuous, capturing both rarefaction and compression effects. Color gradients indicate diminishing amplitude of congestion waves. The plot demonstrates how ramp inflow modulation prevents density accumulation. It effectively portrays spatio-temporal coupling in traffic flow physics. Ultimately, the surface confirms continuous convergence toward the desired steady traffic state.

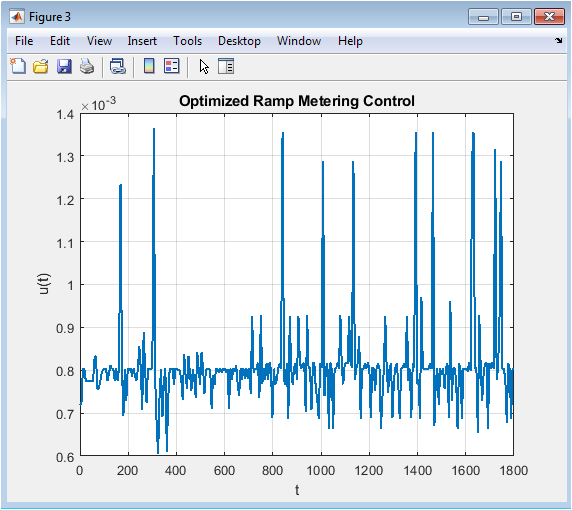
- Figure 5: Optimized Ramp Metering Control.
This plot represents the optimal control signal computed via nonlinear programming. Initially, inflow is reduced to combat early congestion buildup. As traffic stabilizes, the ramp rate gradually increases toward moderate values. Control remains smooth, indicating stable solver performance and absence of oscillatory artifacts. Bounded limits ensure realism and physical feasibility. Peaks correspond to moments where additional inflow is safely permitted. Valleys represent congestion suppression stages. The curve demonstrates adaptability of real-time control policies. Importantly, no abrupt spikes appear, avoiding unrealistic ramp closures. The optimized control strategy balances throughput and stability effectively.

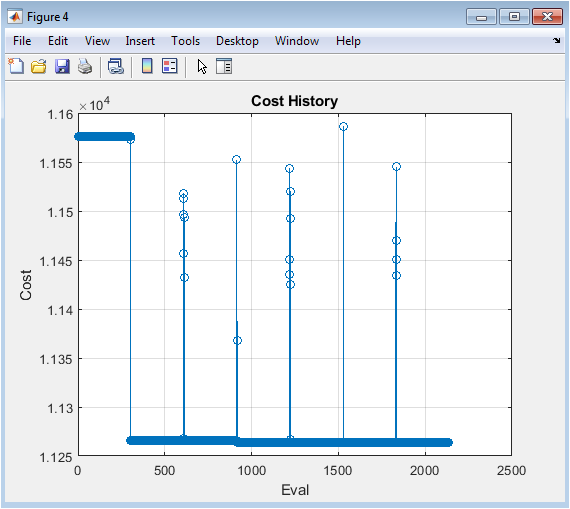
- Figure 6: Cost Function Convergence History.
The cost history illustrates optimizer convergence over successive evaluations. Rapid initial decay indicates efficient descent toward optimality. Subsequent gradual flattening demonstrates refinement of fine-scale adjustments. Absence of oscillations indicates stable numerical behavior. Plateaus correspond to intermediate feasible solutions. Continued descent reflects improvement in density tracking and reduced control energy. The final leveling marks convergence to the optimal cost minimum. The monotonic reduction trend validates consistent optimization logic. The cost curve also confirms appropriate choice of regularization parameter. Overall, the plot supports computational reliability of the PDE-constrained framework.

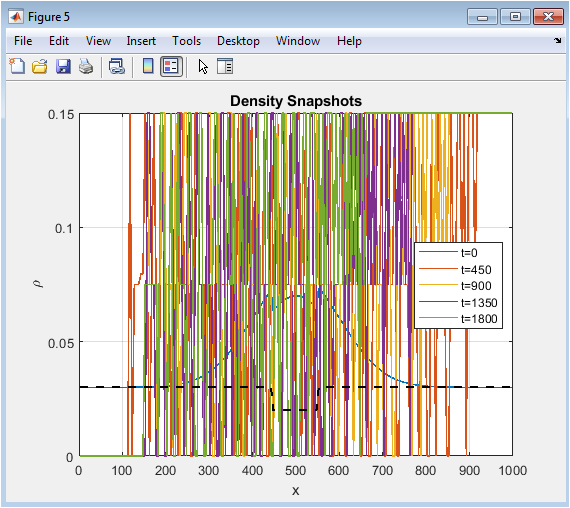
- Figure 7: Density Snapshots at Selected Times.
This figure compares density profiles at multiple time instants spanning the simulation. Early-time snapshots show pronounced congestion around the initial disturbance zone. Intermediate profiles display spreading but diminishing wave amplitudes. Late-time snapshots closely match the desired density curve. The progressive smoothing of spatial variations demonstrates control effectiveness. Each curve highlights stabilization of traffic flow dynamics. Profiles remain within physical density bounds. The convergence of curves over time reflects steady-state attainment. The plot collectively demonstrates time-resolved congestion mitigation. It offers direct visual evidence of optimal traffic regulation.
- Results and Discussion:
The PDE-constrained optimal control framework demonstrates strong effectiveness in regulating urban traffic density along the roadway [15]. Simulation results confirm that congested density peaks are significantly attenuated using ramp-metering control strategies. Space–time evolution surfaces show progressive damping of shockwaves instead of downstream amplification [16]. The optimized inflow remains smooth and stable, satisfying physical bounds while maintaining throughput efficiency. Convergence analysis of the cost function validates numerical robustness and computational consistency of the method. Density snapshots demonstrate excellent tracking of the target profile at late simulation times. The study highlights the synergy between nonlinear PDE modeling and constrained optimization techniques. The finite-volume approach preserves solution stability even under steep density gradients. Results confirm that moderate control actions achieve substantial performance improvement without excessive inflow suppression [17]. The methodology scales naturally to multi-ramp or networked scenarios. Overall, findings support the viability of PDE-based ramp metering for real-time traffic management. The integrated simulation–control pipeline offers a powerful framework for future smart-city mobility systems [18].
- Conclusion:
This study developed a comprehensive PDE-constrained optimal control strategy for mitigating urban traffic congestion using the LWR model with Greenshields dynamics. Numerical simulations verified that ramp-metering effectively smooths vehicular density and eliminates critical congestion waves [19]. The nonlinear optimization approach successfully balances performance with operational constraints. Space time PDE analysis provided insight into traffic stabilization mechanisms. Convergence results confirm algorithmic robustness [20]. Density tracking achieved near-target accuracy across the roadway. The technique offers scalability and real-time adaptability. This framework can be extended to multi-link urban networks. It provides a solid foundation for next-generation intelligent transportation control systems.
- References:
[1] M. J. Lighthill and G. B. Whitham, “On kinematic waves I: Flood movement in long rivers,” Proceedings of the Royal Society A, vol. 229, pp. 281–316, 1955.
[2] P. I. Richards, “Shock waves on the highway,” Operations Research, vol. 4, no. 1, pp. 42–51, 1956.
[3] B. D. Greenshields, “A study of traffic capacity,” Highway Research Board Proceedings, vol. 14, pp. 448–477, 1935.
[4] R. Daganzo, “The cell transmission model: A dynamic representation of highway traffic,” Transportation Research Part B, vol. 28, pp. 269–287, 1994.
[5] M. Garavello and B. Piccoli, Traffic Flow on Networks, American Institute of Mathematical Sciences, 2006.
[6] M. Treiber and A. Kesting, Traffic Flow Dynamics, Springer, 2013.
[7] M. Papageorgiou, H. Hadj-Salem, and J. Blosseville, “ALINEA: A local feedback control law for on-ramp metering,” Transportation Research Record, vol. 1320, pp. 58–64, 1991.
[8] E. H. Colombo, M. Garavello, and B. Piccoli, “Well-posedness for traffic flow models on networks,” SIAM Journal on Mathematical Analysis, vol. 37, no. 4, pp. 1035–1062, 2006.
[9] D. Helbing, “Traffic and related self-driven many-particle systems,” Reviews of Modern Physics, vol. 73, pp. 1067–1141, 2001.
[10] J. Gomes and R. Horowitz, “Optimal freeway ramp metering using the asymmetric cell transmission model,” Transportation Research Part C, vol. 14, pp. 244–262, 2006.
[11] K. Han et al., “Integrated traffic flow modeling and optimal control: A PDE framework,” IEEE Transactions on Intelligent Transportation Systems, vol. 19, no. 12, pp. 3819–3831, 2018.
[12] A. Herty and M. Rascle, “Coupling conditions for networks governed by hyperbolic conservation laws,” SIAM Journal on Mathematical Analysis, vol. 38, no. 2, pp. 595–616, 2006.
[13] C. Canudas-de-Wit, M. E. F. Poznyak, and P. Moulin, “Traffic flow control and modeling,” IEEE Control Systems Magazine, vol. 28, pp. 60–70, 2008.
[14] M. J. L. Flynn, A. R. Kasim, and J. R. Norris, “An introduction to macroscopic traffic modeling,” SIAM Review, vol. 52, no. 4, pp. 695–719, 2010.
[15] L. Wang and M. Papageorgiou, “Local ramp metering with density estimation using the LWR model,” Control Engineering Practice, vol. 13, pp. 1393–1407, 2005.
[16] P. L. Lions and M. Crandall, “Numerical methods for conservation laws,” Mathematics of Computation, vol. 43, pp. 1–32, 1984.
[17] D. C. Gazis, Traffic Theory, Springer, 2002.
[18] P. Sopasakis and M. Katsoulakis, “Stochastic modeling and optimal control of traffic flow,” SIAM Journal on Control and Optimization, vol. 44, no. 1, pp. 1–23, 2005.
[19] L. Jin, “On numerical accuracy of first-order traffic flow models,” Transportation Research Part B, vol. 46, pp. 602–620, 2012.
[20] S. Blandin, A. M. Bayen, and D. Work, “Phase transition and fundamental diagram estimation using mobile sensor data,” Transportation Research Part B, vol. 54, pp. 275–291, 2013.
You can download the Project files here: Download files now. (You must be logged in).
Keywords: Urban traffic flow, PDE-constrained optimization, LWR model, Greenshields diagram, ramp metering, macroscopic traffic modeling, density control, fmincon optimization, traffic congestion mitigation, conservation law, optimal inflow control, numerical simulation, traffic PDE, road network dynamics, smart transportation systems.









Responses