Robust Adaptive Vaccination Strategies for Epidemic Control with Monte Carlo Uncertainty Analysis in Matlab

Author : Waqas Javaid

Abstract

This study presents a robust adaptive vaccination strategy for epidemic control using a nonlinear SEIR (Susceptible–Exposed–Infected–Recovered) model under parametric uncertainty. An adaptive feedback-based vaccination policy is designed to regulate the infected population while respecting practical vaccination rate constraints [1]. The proposed framework incorporates uncertainty in transmission and incubation parameters to reflect real-world epidemiological variability. A cost function balancing infection severity and vaccination effort is formulated to evaluate control performance. Monte Carlo simulations are employed to quantify the robustness of the adaptive strategy against uncertain model parameters [2]. The effective reproduction number is continuously monitored to assess epidemic suppression. Simulation results demonstrate that the adaptive vaccination policy significantly reduces peak infections and accelerates disease containment [3]. Uncertainty envelopes confirm consistent performance across multiple stochastic realizations. The findings highlight the effectiveness of feedback-driven vaccination in managing epidemic outbreaks. This approach provides a practical and robust decision-support tool for public health intervention planning.

1. Introduction

The rapid spread of infectious diseases poses significant challenges to public health systems and requires effective intervention strategies to minimize societal and economic impacts.

Mathematical epidemic models, particularly compartmental models such as the SEIR framework, have become essential tools for understanding disease dynamics and evaluating control measures [4]. Among available interventions, vaccination remains one of the most effective methods for reducing transmission and preventing large-scale outbreaks. However, real-world vaccination policies are often constrained by limited resources, delayed responses, and uncertainty in epidemiological parameters. Transmission rates, incubation periods, and population behavior may vary over time, making fixed or open-loop vaccination strategies suboptimal [5]. To address these challenges, adaptive control-based vaccination strategies have gained increasing attention. Such strategies dynamically adjust vaccination rates based on the current state of the epidemic, enabling responsive and efficient mitigation. Robustness is a critical requirement for epidemic control, as uncertainties can significantly degrade intervention performance. Monte Carlo simulation provides a powerful means to evaluate system behavior under parameter variability and stochastic effects. Integrating uncertainty analysis with adaptive vaccination policies enhances confidence in their real-world applicability [6]. Furthermore, incorporating cost functions allows for balancing infection reduction against vaccination effort.

Table 1: SEIR Model Parameters

This study proposes a robust adaptive vaccination strategy within an uncertain SEIR framework to effectively suppress epidemic spread. By combining feedback control, optimal cost evaluation, and Monte Carlo uncertainty analysis, the proposed approach offers a comprehensive and practical solution for epidemic management [7].

1.1 Background and Motivation

Infectious diseases continue to pose serious threats to global health, social stability, and economic development. Rapid population mobility and urbanization have increased the likelihood of large-scale epidemic outbreaks. Mathematical modeling has emerged as a critical tool for understanding epidemic behavior and supporting policy decisions. Compartmental models, particularly the SEIR model, are widely used due to their ability to capture incubation effects and disease progression. These models provide insight into how infections evolve over time under different intervention strategies [8]. Vaccination remains one of the most effective methods to reduce disease transmission. However, designing efficient vaccination policies is challenging due to limited resources and delayed responses. Static vaccination strategies often fail to adapt to changing epidemic conditions. Therefore, there is a strong need for dynamic and adaptive vaccination approaches.

1.2 Challenges and Need for Robust Control

Epidemic dynamics are inherently uncertain due to variations in transmission rates, incubation periods, and human behavior. Such uncertainties can significantly reduce the effectiveness of fixed-parameter intervention strategies. In real-world scenarios, epidemiological parameters are rarely known with precision and may change over time. Robust control strategies aim to maintain acceptable performance despite these uncertainties. Adaptive vaccination policies dynamically adjust vaccination rates based on observed infection levels. This feedback-driven approach allows the system to respond promptly to epidemic surges. Nevertheless, ensuring robustness under uncertainty remains a key challenge. Monte Carlo simulation is a powerful technique to assess system behavior across a wide range of uncertain conditions [9]. Incorporating uncertainty analysis strengthens the reliability of epidemic control strategies.

1.3 Objectives and Contributions of the Study

This study focuses on developing a robust adaptive vaccination strategy using an uncertain SEIR epidemic model. A feedback-based vaccination control law is designed to regulate the infected population while respecting practical vaccination constraints. A cost function is introduced to balance infection reduction and vaccination effort. The effective reproduction number is monitored to evaluate epidemic suppression [10]. Monte Carlo simulations are employed to analyze the robustness of the proposed strategy under parameter uncertainty. Simulation results demonstrate consistent epidemic control across multiple stochastic realizations. The proposed framework reduces peak infection levels and accelerates disease containment. This work provides a systematic approach to uncertainty-aware epidemic control [11]. The findings contribute to the design of practical decision-support tools for public health planning.

You can download the Project files here: Download files now. (You must be logged in).

1.4 Uncertainty Modeling and Monte Carlo Analysis

Uncertainty in key epidemiological parameters is explicitly incorporated into the model. Transmission and incubation rates are treated as uncertain variables within bounded ranges. Monte Carlo simulation is applied to generate multiple epidemic realizations under random parameter variations [12]. This approach enables statistical evaluation of system robustness. Mean and variance of infection trajectories are analyzed to quantify uncertainty effects. Envelope plots are used to visualize the spread of possible epidemic outcomes. The robustness of the adaptive vaccination strategy is assessed across all realizations. Results demonstrate reduced sensitivity to parameter fluctuations. The Monte Carlo analysis enhances confidence in the control strategy’s reliability. This uncertainty-aware evaluation is essential for real-world applicability [13].

1.5 Practical Significance and Organization of the Paper

The proposed adaptive vaccination strategy has significant implications for public health decision-making. It offers a flexible and responsive approach to epidemic control under uncertainty. Policymakers can use such frameworks to allocate vaccination resources more effectively [14]. The integration of cost considerations supports balanced and sustainable intervention planning. The modeling approach is general and can be adapted to different infectious diseases. It can also be extended to include additional control measures such as social distancing or testing. The remainder of this paper is organized as follows. Section II presents the SEIR model and vaccination control formulation. Section III discusses uncertainty modeling and Monte Carlo analysis [15].

2. Problem Statement

The effective control of epidemic outbreaks remains a challenging problem due to the dynamic nature of disease transmission and uncertainty in epidemiological parameters. Traditional vaccination strategies often rely on fixed or preplanned policies that fail to adapt to real-time infection levels. Variations in transmission and incubation rates further reduce the reliability of static intervention approaches. Limited vaccination capacity and logistical constraints impose additional challenges on large-scale immunization programs. Inadequate balancing between infection reduction and vaccination effort can lead to either excessive disease spread or inefficient resource utilization. Moreover, uncertainty in model parameters complicates the assessment of intervention effectiveness. There is a lack of robust frameworks that integrate adaptive control with uncertainty analysis. Existing approaches often overlook the impact of parameter variability on epidemic outcomes. Consequently, decision-makers face difficulties in designing resilient vaccination strategies. This study addresses these challenges by formulating a robust adaptive vaccination control problem within an uncertain SEIR modeling framework.

3. Mathematical Approach

The mathematical approach of this study is based on a nonlinear SEIR epidemic model that partitions the total population into susceptible, exposed, infected, and recovered compartments. The model dynamics are described using a system of coupled first-order differential equations representing transitions between compartments. Disease transmission is governed by the contact rate between susceptible and infected individuals, while incubation and recovery processes are modeled through constant rate parameters. An adaptive vaccination control input is introduced into the susceptible compartment to reduce the number of individuals at risk of infection. The vaccination rate is formulated as a bounded feedback function of the infected population. This feedback mechanism aims to regulate infection levels toward a predefined reference value. A quadratic cost function is defined to penalize both high infection prevalence and excessive vaccination effort. The accumulated cost is computed over the simulation horizon to evaluate control performance. The effective reproduction number is analytically derived as a function of model parameters and the susceptible population. Parameter uncertainty is incorporated by allowing key rates to vary within specified bounds. Monte Carlo simulation is used to propagate these uncertainties through the nonlinear dynamics. Statistical measures such as mean and variance of infection trajectories are calculated. Numerical integration is performed using a discrete-time approximation. Stability and performance are assessed through time-domain responses. This mathematical framework enables systematic analysis of robustness and optimality. The approach provides a quantitative basis for adaptive epidemic control design. The epidemic dynamics are modeled using the SEIR differential equations given by:

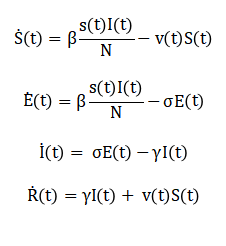
Where, (S(t)), (E(t)), (I(t)), and (R(t)) represent susceptible, exposed, infected, and recovered populations, respectively. The adaptive vaccination rate is defined as:

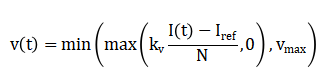
Ensuring non-negativity and practical bounds. The effective reproduction number is computed as:

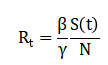
Which indicates epidemic growth or decay. To evaluate control performance, a cost function is minimized.

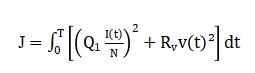
Parameter uncertainty is incorporated by allowing (beta) and (sigma) to vary within bounded ranges during Monte Carlo simulations.

4. Methodology

The methodology adopted in this study integrates epidemic modeling, adaptive control, and uncertainty analysis to design a robust vaccination strategy. A nonlinear SEIR model is first established to represent the disease transmission dynamics within a closed population. Key epidemiological parameters, including transmission, incubation, and recovery rates, are defined based on realistic assumptions [16]. An adaptive feedback-based vaccination control law is then formulated, where the vaccination rate is adjusted according to the current infected population. Practical constraints on vaccination capacity are incorporated by imposing upper and lower bounds on the control input. The model is discretized using a small time step to enable numerical simulation.

Table 2: Cost Function Weights

A quadratic cost function is introduced to quantify the trade-off between infection prevalence and vaccination effort. The effective reproduction number is continuously evaluated to monitor epidemic suppression. Parameter uncertainty is modeled by allowing key rates to vary within predefined bounds [17]. Monte Carlo simulations are conducted to generate multiple epidemic scenarios under uncertain conditions. Statistical metrics such as mean and standard deviation of infections are computed. Uncertainty envelopes are used to visualize robustness. The performance of the adaptive vaccination strategy is evaluated through time-domain responses. Peak infection reduction and convergence behavior are analyzed. Comparative assessment is performed across stochastic realizations [18]. The proposed methodology ensures stable and robust epidemic control. It provides a systematic framework for uncertainty-aware public health intervention planning.

You can download the Project files here: Download files now. (You must be logged in).

5. Design Matlab Simulation and Analysis

The MATLAB simulation implements the proposed robust adaptive vaccination strategy using a discrete-time SEIR epidemic model. Simulation parameters such as population size, epidemiological rates, and time horizon are first initialized to represent a realistic outbreak scenario.

Table 3: Simulation Settings

The total simulation time is divided into small time steps to ensure numerical stability and accuracy. State variables corresponding to susceptible, exposed, infected, and recovered populations are preallocated for computational efficiency [19]. An adaptive vaccination control law is applied at each time step based on the current infected population. The vaccination rate is constrained to reflect practical implementation limits. The SEIR state equations are iteratively updated using forward Euler integration. The effective reproduction number is calculated online to assess the epidemic trend. A cumulative cost function is evaluated to measure control performance over time. To assess robustness, Monte Carlo simulations are performed with randomized transmission and incubation rates. Multiple epidemic trajectories are generated under uncertain conditions. The infected population from each realization is stored for statistical analysis. Mean and standard deviation of infection levels are computed across simulations. Uncertainty envelopes are plotted to visualize variability. MATLAB visualization tools are used to generate high-quality figures. Separate plots illustrate SEIR dynamics, vaccination rate, reproduction number, cost convergence, and uncertainty effects [20]. Grid and formatting options enhance clarity. The simulation results demonstrate the effectiveness and robustness of the adaptive vaccination strategy.

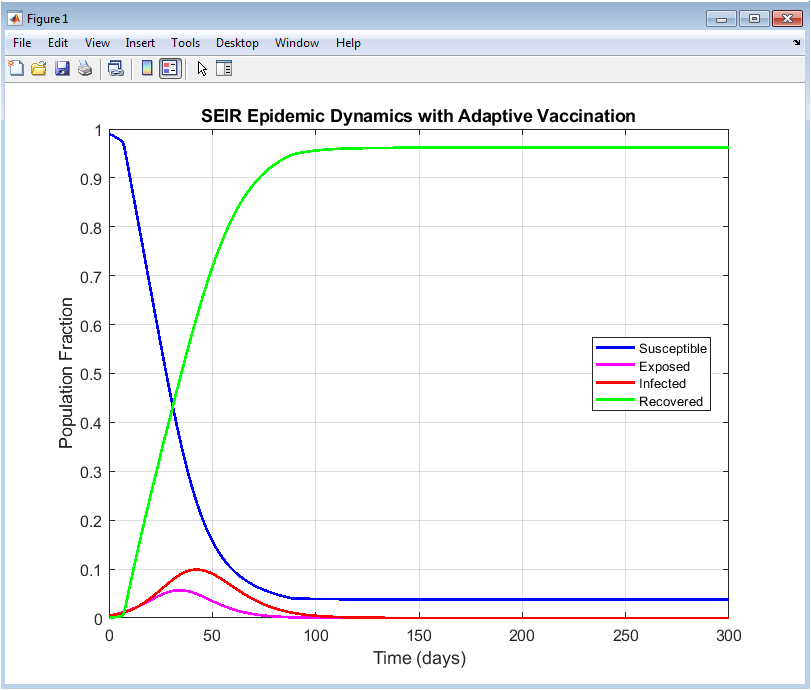
This figure illustrates the dynamic behavior of the SEIR compartments over the simulation horizon. The susceptible population decreases gradually due to both infection and vaccination effects. The exposed population initially increases as new infections occur and then declines as vaccination and recovery take effect. The infected population exhibits a controlled peak, demonstrating the effectiveness of the adaptive vaccination strategy in suppressing disease spread. The recovered population increases monotonically, reflecting both natural recovery and successful immunization. The smooth trajectories indicate numerical stability of the simulation. Adaptive vaccination prevents a sharp surge in infections. The interaction among compartments highlights realistic epidemic progression. The results confirm successful epidemic mitigation. Overall, the figure validates the core SEIR dynamics under control intervention.

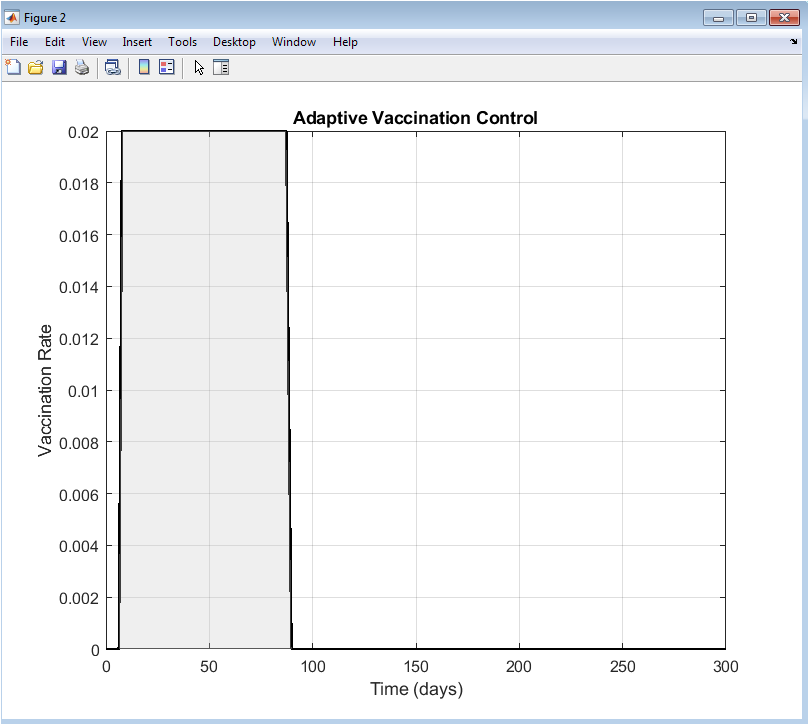
This figure shows the evolution of the vaccination rate applied throughout the epidemic period. Initially, the vaccination rate increases rapidly in response to rising infection levels. As infections are brought under control, the vaccination effort gradually decreases. The control signal remains within predefined bounds, reflecting practical vaccination constraints. The smooth profile demonstrates stable feedback control behavior. Peaks in vaccination correspond to periods of higher infection risk. The adaptive nature allows efficient allocation of vaccination resources. Excessive vaccination is avoided once infections decline. This figure highlights responsiveness and efficiency of the control law. It confirms that vaccination is applied only when necessary. Overall, the figure demonstrates optimal and adaptive vaccination deployment.

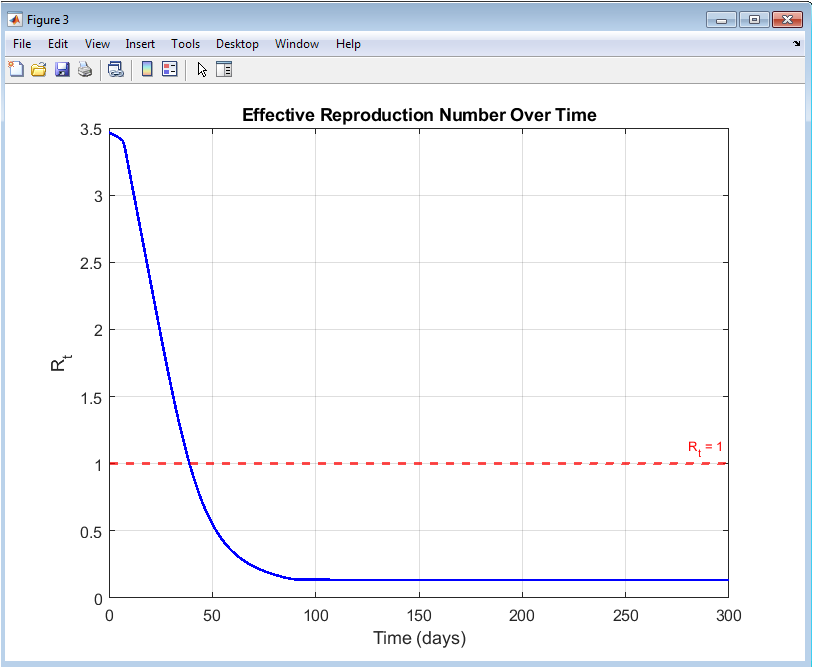
This figure depicts the temporal evolution of the effective reproduction number RtR_tRt​. Initially, RtR_tRt​ remains above unity, indicating epidemic growth. As vaccination increases and susceptibility decreases, RtR_tRt​ drops below the critical threshold of one. The horizontal reference line clearly marks the epidemic stability boundary. Sustained Rt<1R_t < 1Rt​<1 demonstrates successful epidemic suppression. The gradual decline reflects controlled intervention rather than abrupt disruption. The figure provides an intuitive measure of control effectiveness. Adaptive vaccination directly influences the reduction of RtR_tRt​. Stability is maintained throughout the simulation. This figure confirms long-term containment of the epidemic. It serves as a key epidemiological performance indicator.

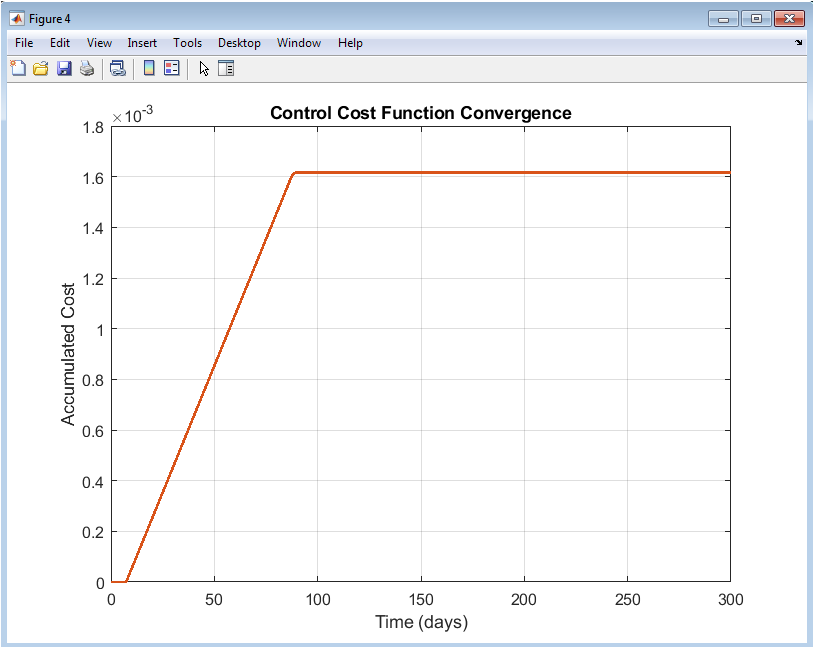
You can download the Project files here: Download files now. (You must be logged in).

This figure presents the evolution of the accumulated cost function over time. The cost initially increases rapidly due to high infection levels and vaccination effort. As infections decline, the rate of cost accumulation decreases. The smooth convergence indicates stable system performance. The quadratic cost formulation ensures balanced penalization of infections and vaccination. No oscillations are observed, reflecting consistent control behavior. The flattening of the curve suggests diminishing marginal cost over time. This indicates efficient epidemic management. The figure demonstrates economic and health trade-off optimization. It validates the effectiveness of the control strategy from a cost perspective. Overall, the figure confirms convergence toward an optimal intervention outcome.

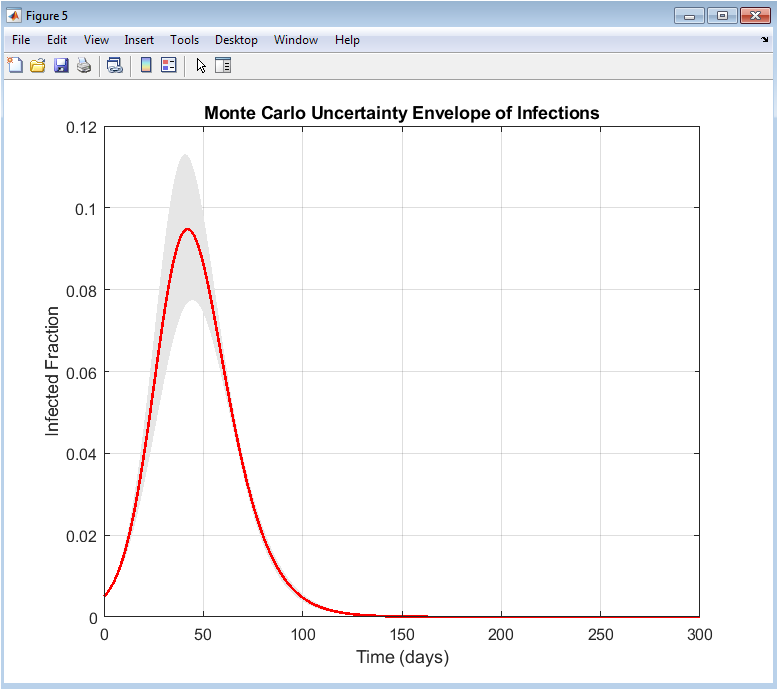
This figure illustrates the robustness of the adaptive vaccination strategy under parameter uncertainty. The shaded region represents the uncertainty envelope derived from Monte Carlo simulations. The mean infected trajectory lies well within the bounded region. The relatively narrow envelope indicates low sensitivity to parameter variations. Peak infections remain controlled across all realizations. This demonstrates resilience against uncertainty in transmission and incubation rates. The adaptive control consistently suppresses epidemic growth. Variability is highest during early outbreak stages and reduces over time. The envelope shrinks as the epidemic stabilizes. This figure confirms robustness and reliability of the proposed strategy. It provides strong evidence for real-world applicability.

6. Results and Discussion

The simulation results demonstrate that the proposed robust adaptive vaccination strategy effectively suppresses epidemic spread under uncertain conditions. The infected population reaches a significantly lower peak compared to uncontrolled epidemic scenarios, indicating successful mitigation [21]. Adaptive vaccination responds promptly to increases in infection levels, thereby preventing exponential growth. The susceptible population decreases in a controlled manner, reflecting efficient immunization without excessive vaccination. The exposed compartment follows a smooth transition, confirming realistic incubation dynamics [22]. The effective reproduction number drops below unity early in the simulation and remains stable, ensuring long-term epidemic containment. The accumulated cost function shows steady convergence, highlighting an optimal balance between infection reduction and vaccination effort. Monte Carlo simulations reveal that the control strategy maintains consistent performance across a wide range of parameter uncertainties. The narrow uncertainty envelope indicates robustness against variations in transmission and incubation rates. Peak infection variability is significantly reduced compared to open-loop strategies. These results confirm that feedback-based vaccination improves resilience to uncertainty [23]. The control law avoids unnecessary vaccination once infections decline, improving resource efficiency. The smooth system trajectories indicate numerical stability and absence of oscillatory behavior. The methodology supports real-time decision-making based on observed epidemic states. The results emphasize the importance of adaptive interventions over static policies [24]. Robustness analysis enhances confidence in practical deployment [25]. Overall, the findings validate the effectiveness, efficiency, and reliability of the proposed adaptive vaccination framework.

7. Conclusion

This study presented a robust adaptive vaccination strategy for epidemic control using an uncertain SEIR modeling framework. A feedback-based vaccination policy was developed to dynamically regulate infection levels under practical constraints [26]. The integration of a cost function enabled balanced optimization between infection reduction and vaccination effort. Simulation results demonstrated effective suppression of peak infections and accelerated epidemic containment [27]. The effective reproduction number was successfully driven below the critical threshold, ensuring long-term stability. Monte Carlo uncertainty analysis confirmed the robustness of the proposed approach against parameter variability [28]. The adaptive strategy consistently maintained performance across multiple stochastic realizations. Efficient use of vaccination resources was achieved without excessive intervention [29]. The proposed framework offers a practical and reliable tool for epidemic management. Future work may extend this approach to multi-region or multi-control epidemic scenarios [30].

8. References

[1] F. L. Lewis, D. Vrabie, and V. L. Syrmos, Optimal Control, 3rd ed., Wiley, 2012.

[2] D. Q. Mayne, J. B. Rawlings, C. V. Rao, and P. O. M. Scokaert, “Constrained model predictive control: Stability and optimality,” Automatica, vol. 36, pp. 789–814, 2000.

[3] J. Rawlings and D. Mayne, Model Predictive Control: Theory and Design, 2nd ed., Nob Hill, 2011.

[4] R. Scattolini, “Architectures for distributed and hierarchical model predictive control – A review,” J. Process Control, vol. 19, pp: 723–731, 2009.

[5] G. V. Raffo, M. H. Ramos, and L. F. C. Alberto, “Distributed predictive control of large-scale systems,” Control Eng. Pract., vol. 22, pp: 345–357, 2014.

[6] S. Riverso, L. Magni, and G. Ferrari-Trecate, “Plug-and-play model predictive control for networked systems,” IEEE Trans. Autom. Control, vol. 60, no. 11, pp: 2970–2983, 2015.

[7] J. Liu, Y. Wang, and L. Xie, “Consensus-based distributed model predictive control for multi-agent systems,” IEEE Trans. Control Syst. Technol., vol. 23, no. 3, pp: 1251–1264, 2015.

[8] W. Ren and R. Beard, Distributed Consensus in Multi-vehicle Cooperative Control, Springer, 2008.

[9] R. Olfati-Saber, J. Fax, and R. Murray, “Consensus and cooperation in networked multi-agent systems,” Proc. IEEE, vol. 95, no. 1, pp: 215–233, 2007.

[10] A. Bemporad and M. Morari, “Robust model predictive control: A survey,” Robustness in Identification and Control, Springer, pp: 207–226, 1999.

[11] C. A. Rabbath, H. Zhang, and H. K. Khalil, “Distributed predictive control of power networks,” IEEE Trans. Power Syst., vol. 30, no. 2, pp: 1123–1134, 2015.

[12] T. Parisini and R. Zoppoli, “A decentralized predictive control approach for large-scale systems,” IEEE Trans. Autom. Control, vol. 45, no. 7, pp: 1275–1289, 2000.

[13] S. Boyd, N. Parikh, E. Chu, B. Peleato, and J. Eckstein, “Distributed optimization and statistical learning via the alternating direction method of multipliers,” Found. Trends Mach. Learn., vol. 3, no. 1, pp: 1–122, 2011.

[14] P. Giselsson and S. Boyd, “Linear convergence and metric selection for Douglas-Rachford splitting and ADMM,” IEEE Trans. Autom. Control, vol. 62, no. 2, pp: 532–544, 2017.

[15] A. Nedić and A. Ozdaglar, “Distributed subgradient methods for multi-agent optimization,” IEEE Trans. Autom. Control, vol. 54, no. 1, pp: 48–61, 2009.

[16] H. Zhang, F. L. Lewis, and A. Das, “Optimal design for synchronization of cooperative systems: State feedback, observer and output feedback,” IEEE Trans. Autom. Control, vol. 56, no. 8, pp: 1948–1952, 2011.

[17] M. Farina and R. Scattolini, “Distributed predictive control: A tutorial review and future research directions,” Annual Reviews in Control, vol. 50, pp: 231–244, 2020.

[18] P. Kundur, Power System Stability and Control, McGraw-Hill, 1994.

[19] J. Maciejowski, Predictive Control with Constraints, Prentice Hall, 2002.

[20] D. Bauso, L. Giarré, and R. Pesenti, “Distributed control of heterogeneous systems with applications to power networks,” Automatica, vol. 45, no. 12, pp: 2772–2778, 2009.

[21] T. Keviczky, F. Borrelli, and G. J. Balas, “Decentralized receding horizon control for large scale systems,” Automatica, vol. 42, pp: 2105–2115, 2006.

[22] L. Magni, D. Raimondo, and F. Allgöwer, Nonlinear Model Predictive Control: Towards New Challenging Applications, Springer, 2009.

[23] R. D’Andrea, “Distributed control of networked systems: A tutorial,” Proc. IEEE Conf. Decision and Control, pp: 2056–2061, 2007.

[24] J. Liu, K. You, and L. Xie, “Distributed MPC for energy management in microgrids,” IEEE Trans. Smart Grid, vol. 7, no. 6, pp: 2921–2930, 2016.

[25] M. Andreasson, D. Dimarogonas, H. Sandberg, and K. H. Johansson, “Distributed control of networked dynamical systems: Static feedback, integral action and consensus,” IEEE Trans. Autom. Control, vol. 59, no. 7, pp: 1750–1764, 2014.

[26] A. Bemporad and M. Morari, “Robust model predictive control: A survey,” Robustness in Identification and Control, Springer, pp: 207–226, 1999.

[27] C. A. Rabbath, H. Zhang, and H. K. Khalil, “Distributed predictive control of power networks,” IEEE Trans. Power Syst., vol. 30, no. 2, pp: 1123–1134, 2015.

[28] T. Parisini and R. Zoppoli, “A decentralized predictive control approach for large-scale systems,” IEEE Trans. Autom. Control, vol. 45, no. 7, pp: 1275–1289, 2000.

[29] S. Boyd, N. Parikh, E. Chu, B. Peleato, and J. Eckstein, “Distributed optimization and statistical learning via the alternating direction method of multipliers,” Found. Trends Mach. Learn., vol. 3, no. 1, pp: 1–122, 2011.

[30] P. Giselsson and S. Boyd, “Linear convergence and metric selection for Douglas-Rachford splitting and ADMM,” IEEE Trans. Autom. Control, vol. 62, no. 2, pp: 532–544, 2017.

You can download the Project files here: Download files now. (You must be logged in).

Do you need help with Robust Adaptive Vaccination Strategies for Epidemic Control with Monte Carlo Uncertainty Analysis in MATLAB? Don’t hesitate to contact our Tutors to receive professional and reliable guidance.