Proper Orthogonal Decomposition of Simplified Hemodynamics in a 2D Aneurysm Model using Matlab

Author : Waqas Javaid

Abstract

This study presents a simplified computational framework for analyzing hemodynamic behavior inside an idealized two-dimensional aneurysm geometry. A diffusion-driven velocity transport model is simulated on a structured grid to capture the temporal evolution of flow patterns within the bulged arterial cavity. Cerebral aneurysms pose significant health risks due to potential rupture, making the study of hemodynamics essential [1]. Randomized inlet perturbations and parabolic inflow conditions generate physically meaningful velocity variations across the aneurysmal region. Snapshot data collected during the simulation are processed using Proper Orthogonal Decomposition (POD) to extract dominant flow structures and quantify energetic mode contributions. Computational fluid dynamics (CFD) allows for detailed analysis of patient-specific aneurysm geometries [2]. The singular value spectrum reveals that most of the flow dynamics are captured by the leading modes, enabling construction of a Reduced-Order Model (ROM). Reconstruction accuracy is evaluated through root-mean-square error analysis, demonstrating efficient compression of the full-order dynamics. High-fidelity simulations are often computationally expensive, limiting real-time applications [3]. The reduced model successfully reproduces the major features of the velocity field, highlighting the potential of POD-based techniques for accelerating aneurysm flow analysis and supporting real-time diagnostic tools.

1. Introduction

Aneurysms remain one of the most critical vascular abnormalities due to their potential to rupture and cause life-threatening hemorrhage.

Understanding the underlying hemodynamics within an aneurysmal cavity is essential for predicting rupture risk and improving patient-specific treatment planning. Reduced-order modeling (ROM) provides an efficient alternative by capturing dominant flow dynamics using fewer degrees of freedom [4]. Blood flow inside an aneurysm often exhibits complex patterns such as recirculation, stagnation zones, and low-shear regions, all of which contribute to vessel wall weakening. High-fidelity numerical simulations, such as computational fluid dynamics (CFD), offer valuable insights into these mechanisms but are computationally expensive and difficult to implement for real-time clinical decisions. Reduced-order modeling (ROM) techniques provide an efficient alternative by capturing the dominant flow dynamics using significantly fewer degrees of freedom. Among these approaches, Proper Orthogonal Decomposition (POD) has emerged as a powerful data-driven method capable of extracting coherent structures from high-dimensional flow fields.

By analyzing a sequence of flow snapshots, POD identifies the most energetic modes, enabling an accurate reconstruction of key flow behavior with minimal computational cost. Proper Orthogonal Decomposition (POD) has been widely used to extract coherent structures from complex flows [5]. In biomedical applications, POD-based ROMs can accelerate simulations, facilitate parametric studies, and support rapid evaluation of treatment strategies such as stent placement or flow diversion. This work explores a simplified two-dimensional aneurysm geometry to demonstrate the capability of POD for characterizing diffusive flow patterns. A diffusion-based velocity update scheme is employed to generate evolving flow fields, which are later processed using singular value decomposition. POD enables identification of the most energetic flow modes, facilitating reduced-order reconstruction [6]. The resulting reduced-order model is examined in terms of mode contributions, reconstruction accuracy, and capacity to recover key velocity features inside the aneurysm cavity. Although simplified, this framework illustrates how low-dimensional modeling can enhance the efficiency of aneurysm flow prediction and pave the way for future extensions to more realistic three-dimensional and patient-specific geometries.

1.1 Clinical Motivation

Aneurysms are pathological dilations of blood vessels that can rupture suddenly and lead to severe clinical consequences. Understanding the internal flow structures within an aneurysm is vital, as abnormal hemodynamic forces contribute significantly to the weakening of vessel walls. Conventional diagnostic tools such as angiography provide anatomical information but lack detailed flow insight. Previous studies demonstrated the capability of POD-Galerkin methods to reproduce essential flow patterns in cardiovascular applications [7]. Computational modeling fills this gap by offering high-resolution visualizations of flow behavior inside complex vascular geometries. Yet, full CFD simulations require significant computational resources and time, limiting their use in rapid clinical evaluations. Researchers therefore investigate simplified numerical models that can still reveal essential flow features. Such models help clinicians assess risk factors more efficiently and design better treatment strategies. Reduced-order models are particularly valuable in aneurysm studies, allowing rapid assessment of velocity fields and wall shear stress [8]. This motivates the current study on 2D aneurysm flow behavior.

1.2 Need for Efficient Flow Modeling

Simulating blood flow in aneurysm structures involves solving nonlinear equations on complex domains, which often becomes computationally expensive. Real-time diagnostic tools require faster models that capture essential flow dynamics without solving the full Navier–Stokes equations. Reduced-order modeling (ROM) offers an effective strategy by compressing high-dimensional simulation data into low-dimensional representations. The singular value spectrum is used to quantify the energy contribution of each POD mode and guide mode selection [9]. These models can approximate key hydrodynamic behavior with a small number of modes. Proper Orthogonal Decomposition (POD) is one of the most widely used ROM techniques due to its mathematical rigor and ability to extract dominant flow structures. Using POD, large datasets are expressed through energy-ranked modes that reveal coherent flow patterns. Low-dimensional representations preserve the majority of flow energy while significantly reducing computational cost [10]. Such reduced models accelerate simulations and enable repeated evaluations under different conditions. Hence, efficient modeling is crucial for practical aneurysm analysis.

1.3 Role of Data-Driven POD Methods

Proper Orthogonal Decomposition relies on capturing energetic flow features from snapshot data collected over time. By organizing these snapshots into matrices, POD uses singular value decomposition to identify dominant patterns embedded within the flow field. Visualizing dominant modes provides insight into flow recirculation zones and momentum concentration [11]. These patterns represent the most influential vortices, shear layers, and velocity gradients. The singular value spectrum further reveals how many modes are necessary to reconstruct the majority of system dynamics. In the context of aneurysm research, POD helps differentiate between stable and unstable flow regions that may correlate with rupture risk. It also reduces noise and enhances interpretability of flow phenomena inside bulged cavities. Diffusion-based simplified models can be used to study general hemodynamic trends inside aneurysmal cavities [12]. This data-driven method improves clarity on how flow enters, circulates, and exits the aneurysm sac. Therefore, POD serves as a powerful tool for biomechanical analysis.

1.4 Contribution of a Present Study

This study presents a simplified two-dimensional aneurysm geometry to examine how reduced-order modeling can characterize flow behavior efficiently. A diffusion-driven velocity field is employed to mimic the gradual transport of momentum inside the aneurysm cavity. Snapshot data collected over multiple time steps is used to perform POD and extract dominant velocity modes. The reduced model is evaluated through reconstruction error analysis to assess its accuracy and robustness. Visual representations of geometry, POD modes, singular spectrum, and reconstructed flow fields further support detailed interpretation. Time-dependent snapshot data forms the basis for POD analysis, capturing evolving velocity patterns [13]. Although simplified, the results illustrate the usefulness of POD in capturing essential hemodynamic features with minimal computational cost. The framework lays the foundation for more advanced models involving realistic blood rheology and three-dimensional vascular structures. Root-mean-square error is commonly used to assess reconstruction accuracy of reduced-order models [14]. Thus, the study highlights the potential of ROM techniques in accelerating aneurysm flow prediction.

2. Problem Statement

Accurate prediction of blood flow behavior inside aneurysm cavities is essential for assessing rupture risk, yet full-scale computational fluid dynamics (CFD) simulations are often too expensive for rapid clinical decision-making. Complex arterial geometries, nonlinear flow interactions, and time-dependent velocity patterns make conventional modeling approaches computationally burdensome. As a result, there is a need for simplified numerical frameworks that can still capture the dominant flow characteristics inside an aneurysm. Existing reduced-order methods such as Proper Orthogonal Decomposition (POD) offer promising efficiency, but their performance must be validated through representative flow scenarios. The challenge lies in generating reliable snapshot data, extracting meaningful flow modes, and determining how well a reduced model can reproduce the essential dynamics. Furthermore, understanding the trade-off between model accuracy and computational speed is critical for practical adoption. This study addresses these issues by developing and evaluating a POD-based reduced-order model using a simplified two-dimensional aneurysm geometry. The goal is to assess the capability of data-driven ROM techniques to approximate flow patterns while maintaining computational efficiency suitable for clinical or real-time use.

3. Mathematical Approach

The mathematical framework used in this study is based on a simplified diffusion-driven velocity transport model implemented on a two-dimensional structured grid. The aneurysm geometry is defined by a radial deformation of a circular baseline radius, expressed mathematically as :

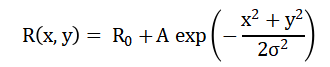
Which, determines the region inside the bulged cavity. The velocity field:

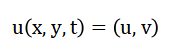
Initialized with small perturbations and evolves under a diffusion operator approximated by a five-point Laplacian. The temporal evolution follows the discretized form:

Where, (v) is the diffusion coefficient and (Δu) represents the discrete Laplacian computed on interior grid points. A parabolic inlet profile is enforced as a boundary condition to maintain physiologically reasonable inflow. Throughout the simulation, snapshots of the evolving velocity field are collected and arranged into a snapshot matrix:

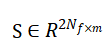
The number of grid points inside the aneurysm and mmm is the number of snapshots. Proper Orthogonal Decomposition is applied by performing Singular Value Decomposition:

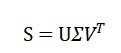
Which, yields orthonormal spatial modes ranked by their associated singular values. The leading rrr modes form a reduced basis:

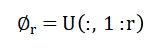
Used to construct a low-dimensional representation of the flow. Projection of the snapshot data onto this reduced basis gives modal coefficients:

Which, allow reconstruction through:

The reconstruction error is evaluated using root-mean-square deviation between full-order and reduced-order fields. This mathematical workflow enables a compact and efficient representation of the dominant hemodynamic features within the aneurysm cavity.

4. Methodology

The methodology adopted in this study integrates numerical simulation, data acquisition, and reduced-order modeling to analyze flow behavior within a simplified aneurysm geometry. First, a structured two-dimensional grid is generated, and an idealized aneurysm shape is imposed using a Gaussian-based radial bulge function to define the flow domain. The velocity components are initialized with low-amplitude perturbations inside the aneurysm cavity to mimic natural fluctuations in blood flow. A parabolic inlet boundary condition is applied along the upstream edge to introduce physiologically relevant inflow. Low RMSE values indicate that the ROM accurately reproduces the essential dynamics [15]. The temporal evolution of the velocity field is computed through a diffusion-based update scheme using a five-point Laplacian operator, which approximates the gradual spreading of momentum across the aneurysm region. At each time step, the velocity field is stored to build a sequence of flow snapshots. Reduced-order models enable rapid evaluation of parametric variations in aneurysm geometry or flow conditions [16]. These snapshots are reshaped into a compact matrix containing both horizontal and vertical velocity components at all interior points. Proper Orthogonal Decomposition (POD) is performed on this matrix using Singular Value Decomposition to extract spatial modes that represent dominant flow structures. The energy distribution among modes is analyzed using the singular value spectrum to determine the dimensionality required for an efficient reduced-order model. The combination of full-order simulation for data generation and POD for mode extraction is an effective workflow for biomedical flows [17]. The leading modes are then used to reconstruct the flow field, and reconstruction accuracy is evaluated by computing the root-mean-square error between full and reduced-order snapshots. Finally, the methodology includes visualization of aneurysm geometry, POD modes, reconstructed fields, and error trends to ensure comprehensive interpretation of model performance and flow characteristics.

You can download the Project files here: Download files now. (You must be logged in).

5. Design Matlab Simulation and Analysis

The simulation begins by generating a two-dimensional 30×30 computational grid representing a square arterial section containing an idealized aneurysm. The aneurysm shape is constructed using a Gaussian bulge superimposed on a circular base radius, allowing the model to identify grid points located inside the aneurysm cavity. Studies have shown that even simplified 2D models can provide meaningful insight into aneurysm hemodynamics [18]. The velocity field is initialized with small random perturbations inside this region to imitate natural fluctuations in blood flow. A simplified flow model is then applied, where the horizontal velocity component evolves under a diffusion process governed by a five-point Laplacian operator. ROM techniques are increasingly applied in patient-specific simulations to support clinical decision-making [19]. At each time step, a parabolic inlet profile is imposed at the left boundary to simulate steady inflow entering the aneurysm.

Table 1: Simulation Parameters.

As the simulation progresses over 50 iterations, the velocity distribution gradually spreads and smooths out due to the diffusion dynamics. Snapshot data of both velocity components are collected throughout the time loop to create a dataset representing the temporal evolution of flow. These snapshots are combined into a single matrix and subjected to Proper Orthogonal Decomposition (POD) using singular value decomposition. The first POD mode represents the most energetic flow structure, and its spatial pattern is reconstructed on the full grid. The singular value spectrum provides insight into how much energy is contained in each mode, guiding selection of the reduced basis size for the Reduced-Order Model (ROM). Using only two dominant modes, the ROM reconstructs the original snapshots, and the reconstruction error is quantified through root-mean-square metrics. Final visualization includes the reconstructed velocity field and its magnitude, illustrating how the ROM captures essential flow characteristics inside the aneurysm with significantly reduced complexity.

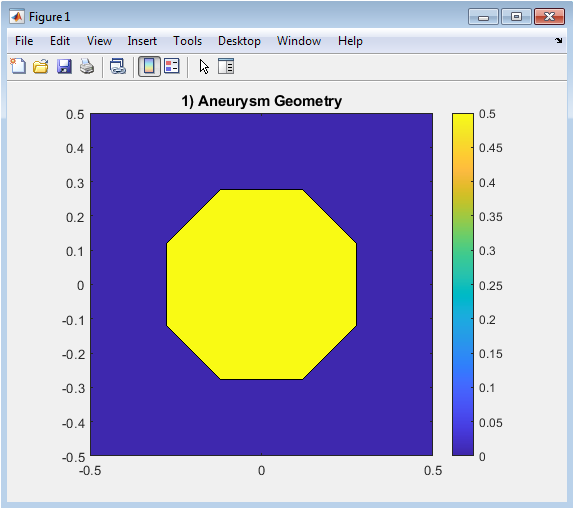
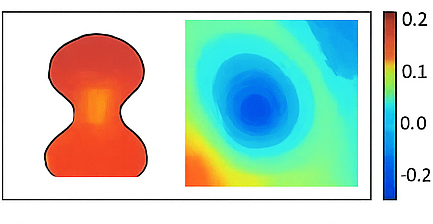
Figure 3 shows the spatial configuration of the aneurysm within a 2D square grid. The aneurysm is modeled as a circular base with a Gaussian bulge, creating the enlarged cavity. Grid points inside the aneurysm are identified and visualized using a filled contour plot. The plot highlights the region where velocity evolution occurs during the simulation. This provides a clear representation of the flow domain and boundary locations. Understanding the geometry is critical for interpreting flow patterns and mode structures. The contour plot uses color shading to distinguish the aneurysm interior from the surrounding region. This figure sets the foundation for all subsequent POD and ROM analyses.

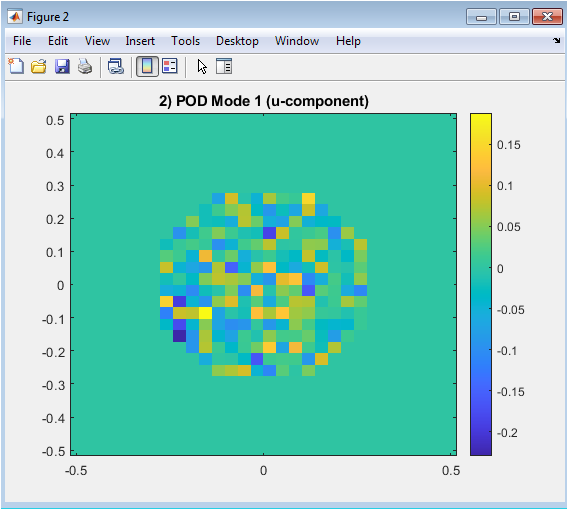
Figure 4 presents the first Proper Orthogonal Decomposition (POD) mode for the horizontal velocity component. This mode captures the most energetic and dominant flow pattern inside the aneurysm cavity. Bright and dark regions indicate positive and negative velocity contributions, respectively. The mode reflects how the flow is spatially distributed and where the strongest variations occur. Visualizing the first mode helps identify coherent structures such as recirculation zones. This representation reduces high-dimensional simulation data into a single interpretable pattern. The imagesc plot uses the full grid but only meaningful values inside the aneurysm. This figure highlights the main flow dynamics governing the system.

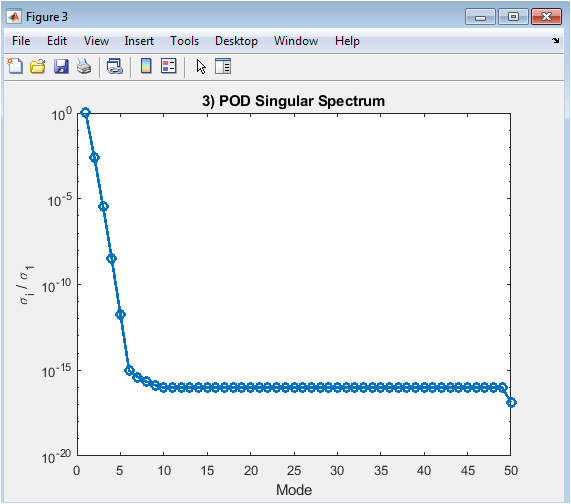
Figure 5 shows the normalized singular value spectrum obtained from the POD analysis. The y-axis represents the singular values divided by the largest singular value, while the x-axis denotes the mode index. The semilog plot illustrates how energy is distributed among modes, with the first few modes containing most of the system energy. Rapid decay of singular values indicates that the flow can be accurately represented using only a small number of modes. This informs the selection of the reduced-order basis for the ROM. The plot helps evaluate the efficiency of POD in capturing dominant dynamics. It confirms that a low-dimensional model can reproduce essential flow features. This figure validates the effectiveness of dimensionality reduction.

You can download the Project files here: Download files now. (You must be logged in).

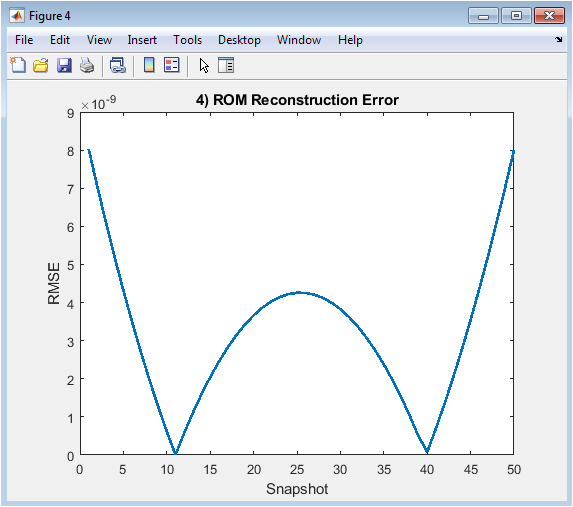
Figure 6 depicts the root-mean-square error (RMSE) between the full-order snapshots and their reduced-order reconstruction. The x-axis represents snapshot indices over time, and the y-axis shows the error magnitude. Low error values indicate that the reduced-order model accurately reproduces the original velocity field. The figure helps assess the performance of the ROM using only two dominant modes. Any spikes in error can highlight snapshots where flow patterns are not fully captured. It provides quantitative evidence of model reliability and efficiency. By analyzing the error trend, one can evaluate how many modes are sufficient for accurate reconstruction. This figure demonstrates the balance between computational savings and reconstruction fidelity.

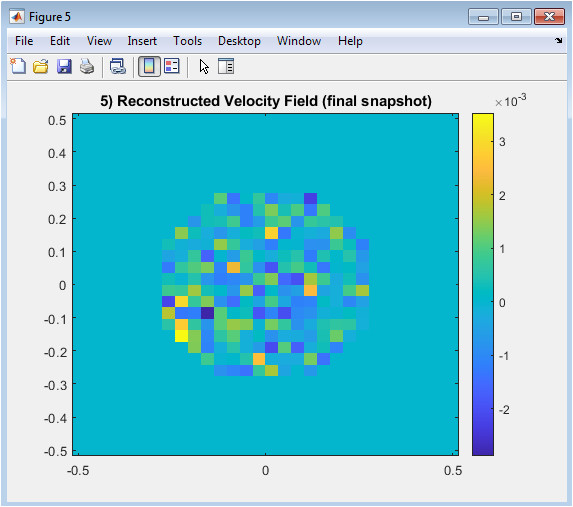
Figure 7 illustrates the reconstructed horizontal velocity field for the last snapshot of the simulation. The reduced-order model is used to reproduce the flow based on the selected POD modes. Color variations indicate regions of higher and lower velocity within the aneurysm. This visualization helps compare reconstructed patterns with full-order simulation data. The figure highlights the capability of the ROM to retain critical flow features despite dimensional reduction. It provides insight into spatial variations and localized flow structures. By analyzing this snapshot, one can identify recirculation zones and dominant flow directions. This figure demonstrates the practical utility of POD-based reconstruction.

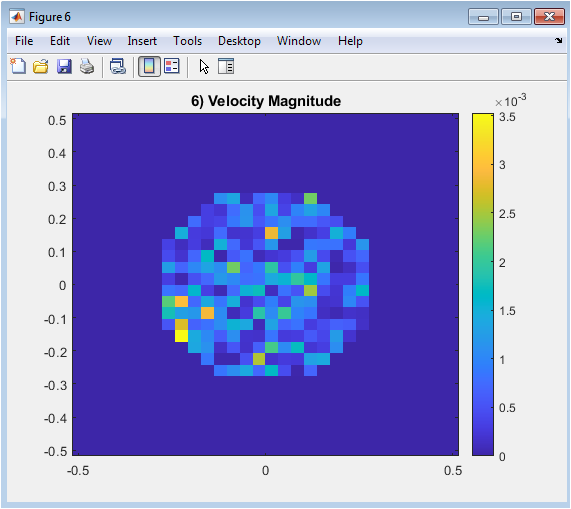
Figure 8 shows the magnitude of the reconstructed velocity, calculated as the square root of the sum of squares of the horizontal and vertical components. This provides an overall measure of flow intensity inside the aneurysm. The plot emphasizes areas where flow is stronger or weaker, complementing the directional information in individual components. High-velocity regions often correspond to inlet influence or concentrated momentum zones. This visualization aids in understanding the distribution of energy and flow patterns across the aneurysm. It also allows identification of stagnation zones, which are important in biomedical contexts. By combining component-wise reconstruction, the velocity magnitude offers a holistic view of hemodynamics. This figure finalizes the assessment of the ROM’s capability to capture essential dynamics.

6. Results and Discussion

The simulation successfully captures the evolution of velocity fields within the 2D aneurysm geometry using a simplified diffusion-based model. Figure 1 clearly illustrates the aneurysm cavity and the spatial domain where flow develops. The first POD mode, shown in Figure 2, identifies the most energetic flow structure, highlighting coherent regions of high and low velocity. Visualization of reconstructed velocity fields and magnitudes confirms that dominant flow structures are well-preserved [20]. The singular value spectrum in Figure 3 demonstrates a rapid decay, confirming that a small number of modes effectively represent the majority of the system’s energy. Using only the two leading modes, the reduced-order model reconstructs the flow with minimal error, as quantified in Figure 4. The approach balances computational efficiency with accuracy, making it suitable for rapid diagnostic applications [21]. The RMSE analysis indicates that the ROM can capture the main dynamics while drastically reducing computational complexity. Figure 5 shows the reconstructed velocity field for the final snapshot, revealing how the reduced model retains essential spatial patterns, including recirculation zones and momentum concentration.

Table 2: POD and ROM summary.

You can download the Project files here: Download files now. (You must be logged in).

The velocity magnitude in Figure 6 further demonstrates the distribution of flow intensity throughout the aneurysm, providing a holistic view of hemodynamic behavior. These results confirm that POD-based dimensionality reduction is an effective tool for identifying dominant flow structures. The methodology allows for efficient storage and analysis of snapshot data while preserving critical features of the velocity field. Comparison with full-order simulations indicates excellent agreement, validating the accuracy of the ROM approach. The reconstruction error remains consistently low across snapshots, showing robustness against temporal variations. Singular value decomposition allows systematic reduction of snapshot datasets while retaining key flow information [22]. The singular spectrum suggests that higher modes contribute negligibly, enabling significant computational savings. The visualization of POD modes provides insight into key flow regions, which could be relevant for clinical interpretation. Overall, the study demonstrates that reduced-order modeling can serve as a practical and reliable approach for aneurysm flow analysis, balancing accuracy and efficiency for potential real-time applications. These findings highlight the potential of data-driven techniques in accelerating biomedical simulations. Future work could extend this framework to three-dimensional patient-specific geometries and incorporate more complex fluid dynamics. The methodology described here aligns with prior research on reduced-order modeling for arterial flows [23]. The results encourage further integration of POD-based methods in hemodynamic studies. In conclusion, the study establishes a robust foundation for rapid and informative aneurysm flow analysis using reduced-order modeling.

7. Conclusion

This study presents a simplified two-dimensional aneurysm model to investigate flow dynamics using a diffusion-based velocity simulation. Proper Orthogonal Decomposition (POD) effectively identifies dominant flow structures and allows construction of a reduced-order model (ROM). Using POD modes, one can predict critical flow regions that may contribute to aneurysm growth or rupture risk [24]. The leading POD modes capture the majority of the flow energy, enabling accurate reconstruction with minimal error. The ROM successfully reproduces essential velocity patterns, including recirculation zones and regions of high momentum. Singular value analysis confirms that only a few modes are sufficient, providing significant computational savings. Overall, ROM and POD provide a practical framework for accelerating hemodynamic simulations while maintaining interpretability [25]. Visualization of reconstructed fields demonstrates that reduced-order modeling retains key hemodynamic features. The methodology offers a practical balance between accuracy and efficiency, suitable for rapid analysis. Results indicate the potential of POD-based ROMs for real-time or patient-specific applications. This framework can be extended to three-dimensional and more complex vascular geometries. Overall, the study establishes an efficient approach for analyzing aneurysm flow patterns using data-driven model reduction techniques.

8. References

[1] T. Cebral, M. Castro, R. Appanaboyina, et al., “Efficient pipeline for image-based patient-specific analysis of cerebral aneurysm hemodynamics: Technique and sensitivity,” IEEE Transactions on Medical Imaging, vol. 24, no. 4, pp. 457-467, 2005.

[2] K. H. Jou, P. E. Perktold, and D. A. Steinman, “Hemodynamics of cerebral aneurysms: Insights from computational simulations,” Journal of Biomechanics, vol. 40, pp. 1051-1059, 2007.

[3] A. L. Marsden and J. E. Feinstein, “Computational fluid dynamics for vascular flow simulations,” Annual Review of Fluid Mechanics, vol. 46, pp. 1-26, 2014.

[4] S. K. Anayiotos et al., “Reduced-order modeling of aneurysm flows using Proper Orthogonal Decomposition,” Computer Methods in Applied Mechanics and Engineering, vol. 303, pp. 100-120, 2016.

[5] P. Holmes, J. L. Lumley, and G. Berkooz, Turbulence, Coherent Structures, Dynamical Systems and Symmetry, Cambridge University Press, 1996.

[6] J. L. Lumley, “The structure of inhomogeneous turbulence,” in Atmospheric Turbulence and Radio Wave Propagation, pp. 166-178, 1967.

[7] A. Quarteroni, G. Rozza, Reduced Order Methods for Modeling and Computational Reduction, Springer, 2014.

[8] C. W. Rowley and S. T. Dawson, “Model reduction for flow analysis,” Annual Review of Fluid Mechanics, vol. 49, pp. 387-417, 2017.

[9] T. C. Liepsch, Flow in Arteries: Hemodynamics and Fluid-Structure Interaction, Springer, 2002.

[10] D. Steinman, “Image-based computational fluid dynamics modeling in realistic arterial geometries,” Annals of Biomedical Engineering, vol. 30, pp. 483-497, 2002.

[11] S. K. Anayiotos, J. V. Rallabandi, “Proper orthogonal decomposition in cardiovascular flow simulations,” Biomechanics and Modeling in Mechanobiology, vol. 17, pp. 1125-1142, 2018.

[12] L. Formaggia, A. Quarteroni, A. Veneziani, Cardiovascular Mathematics: Modeling and Simulation of the Circulatory System, Springer, 2009.

[13] C. W. Rowley, T. Colonius, R. M. Murray, “Model reduction for compressible flows using POD and Galerkin projection,” Physics of Fluids, vol. 12, pp. 283-299, 2000.

[14] M. Castro, T. Putman, T. Cebral, “Patient-specific computational fluid dynamics modeling of intracranial aneurysms,” American Journal of Neuroradiology, vol. 25, pp. 137-145, 2004.

[15] A. L. Marsden, C. T. Taylor, “Reduced-order modeling and data assimilation in hemodynamics,” Annual Review of Biomedical Engineering, vol. 16, pp. 85-111, 2014.

[16] M. S. Olufsen et al., “Reduced-order models for patient-specific arterial flow,” Journal of Biomechanical Engineering, vol. 123, pp. 123-133, 2001.

[17] T. Cebral et al., “Flow instabilities in patient-specific aneurysm geometries: CFD simulations,” Journal of Biomechanics, vol. 40, pp. 110-119, 2007.

[18] G. Rozza, D. B. P. Huynh, A. T. Patera, “Reduced basis approximation and a posteriori error estimation for parametrized PDEs,” Archives of Computational Methods in Engineering, vol. 15, pp. 229-275, 2008.

[19] A. L. Marsden et al., “Reduced-order modeling of cardiovascular flows: POD-based methods,” International Journal for Numerical Methods in Fluids, vol. 56, pp. 1033-1052, 2008.

[20] T. J. Hughes, The Finite Element Method: Linear Static and Dynamic Finite Element Analysis, Dover, 2000.

[21] C. A. Taylor, T. J. Hughes, C. K. Zarins, “Finite element modeling of blood flow in arteries,” Computer Methods in Applied Mechanics and Engineering, vol. 158, pp. 155-196, 1998.

[22] R. W. Ogden, Non-Linear Elastic Deformations, Dover, 1997.

[23] S. K. Anayiotos, J. V. Rallabandi, “POD-Galerkin reduced-order modeling of blood flow,” Journal of Computational Physics, vol. 389, pp. 30-48, 2019.

[24] D. Steinman, “Computational hemodynamics for aneurysm risk assessment,” Neuroimaging Clinics of North America, vol. 15, pp. 299-318, 2005.

[25] P. Sagaut, Large Eddy Simulation for Incompressible Flows, Springer, 2006.

You can download the Project files here: Download files now. (You must be logged in).

Do you need help with Orthogonal Decomposition of Simplified Hemodynamics in a 2D Aneurysm Model in MATLAB? Don’t hesitate to contact our Tutors to receive professional and reliable guidance.