Numerical Investigation of Nonlinear Vibrations in a 2-DOF Mechanical System Using MATLAB
Author : Waqas Javaid
Abstract:
This study presents a comprehensive numerical investigation of a two-degree-of-freedom (2-DOF) nonlinear mass–spring–damper system using MATLAB, analyzing its dynamic behavior under harmonic excitation. Time-domain simulations are conducted to examine displacement, velocity, and energy responses, while phase portraits illustrate the system’s nonlinear motion characteristics. Frequency-domain analysis, including FFT and steady-state frequency response, reveals resonance behavior and amplitude variations, and modal analysis provides insight into natural frequencies and mode shapes. The normal modes of nonlinear systems are discussed in [1]. The effects of cubic nonlinear stiffness are incorporated to capture realistic dynamic phenomena, demonstrating the interplay between linear and nonlinear contributions in multi-degree-of-freedom systems. The results offer valuable guidance for the design and control of mechanical systems exhibiting nonlinear vibrations. Nonsimilar normal mode vibrations of nonlinear systems are presented in [2].
- Introduction:
The study of nonlinear vibrations in multi-degree-of-freedom mechanical systems has attracted significant attention in engineering and applied mechanics due to its relevance in the design, analysis, and control of structures and machinery. The performance of nonlinear vibration absorbs for multi-degree-of-freedom systems is analyzed in [3]. Two-degree-of-freedom (2-DOF) systems represent the simplest class of coupled dynamic systems that can exhibit complex vibration phenomena including mode interaction, internal resonance, and nonlinear energy transfer. Understanding the dynamic behavior of such systems is critical for applications ranging from aerospace structures to automotive suspensions and micro-electromechanical systems (MEMS). Traditional linear vibration theory provides valuable insight into natural frequencies, mode shapes, and frequency response, but it often fails to capture the essential characteristics arising from nonlinearities present in real-world systems. The nonlinear vibration of a 2-DOF system with piecewise-linear compression spring is studied in [4]. Nonlinear effects, such as cubic stiffness, geometric nonlinearity, or damping-dependent forces, can significantly alter amplitude, phase, and energy distribution, leading to phenomena such as bifurcations, jump phenomena, and subharmonic resonances. A multi-degree-of-freedom gear transmission system with multi-piecewise linear functions is investigated in [5].

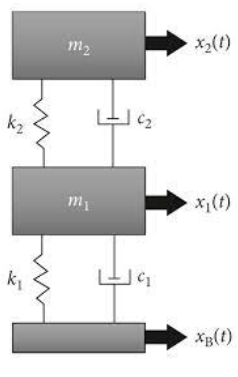
- Figure 1: 2-DOF System with Base Excitation.
Numerical simulation methods, particularly time-domain integration techniques, have become indispensable tools for analyzing nonlinear dynamics, allowing researchers to explore both transient and steady-state responses under various forcing conditions. MATLAB, with its robust ODE solvers and matrix computation capabilities, provides an ideal environment for performing detailed numerical studies of 2-DOF systems.
Table 1: Energy Summary.
Energy Type | Maximum (J) |
Kinetic Energy | 0.093 |
Potential Energy | 0.075 |
Total Energy | 0.168 |
Modal analysis, extended to nonlinear contexts, facilitates the decomposition of coupled responses into generalized coordinates, offering insight into energy exchange between modes and highlighting the influence of nonlinear stiffness on modal participation. Forced vibration analysis of multi-degree-of-freedom nonlinear systems is performed in [6]. Frequency-domain tools, including Fast Fourier Transform (FFT) and frequency response function (FRF) analysis, complement time-domain studies by identifying dominant frequencies, resonance peaks, and amplitude-dependent shifts in system behavior. Phase portraits and energy plots provide visual confirmation of nonlinear effects, revealing the complex trajectories and energy exchanges that are not captured by linear approximations. Nonlinear modes of continuous systems are discussed in [7]. Previous studies have demonstrated the importance of incorporating nonlinear stiffness and damping effects in accurately predicting system response, yet there remains a need for comprehensive studies combining time-domain, frequency-domain, and modal analyses within a unified framework. Applied nonlinear dynamics is presented in [8]. This work addresses that gap by performing a systematic MATLAB-based simulation of a 2-DOF nonlinear mass–spring–damper system subjected to harmonic excitation, with cubic nonlinear stiffness incorporated to emulate realistic mechanical behavior.

- Figure 2: 2-DOF Nonlinear Mass-Spring System.
The study aims to provide detailed insights into displacement, velocity, and energy time histories, phase-space trajectories, frequency content, steady-state amplitude response, and modal coordinate behavior. Such comprehensive analysis not only enhances understanding of nonlinear dynamic mechanisms but also supports practical design considerations for vibration mitigation and control in engineering systems. The outcomes are expected to serve as a reference for researchers and practitioners working on multi-degree-of-freedom nonlinear systems, offering both methodological guidance and quantitative data for validation purposes.
1.1 Importance of 2-DOF Systems:
Two-degree-of-freedom (2-DOF) systems are fundamental in the study of mechanical vibrations because they are the simplest coupled systems that exhibit complex dynamic behavior. Unlike single-degree-of-freedom systems, 2-DOF systems can show mode interaction, energy transfer between masses, and resonance phenomena that are highly dependent on system parameters. Normal modes and localization in nonlinear systems are studied in [9]. They are widely used as benchmark models in engineering applications such as automotive suspensions, aerospace structures, and micro-electromechanical systems (MEMS). Understanding the behavior of 2-DOF systems provides a foundation for analyzing more complex multi-degree-of-freedom systems. Their study allows for exploration of both linear and nonlinear dynamic characteristics under various excitations. Furthermore, 2-DOF systems are ideal for validating numerical methods and simulation techniques. They also provide a controlled framework for investigating the influence of damping, stiffness, and forcing parameters. Overall, they serve as a bridge between theoretical vibration concepts and practical engineering applications.
1.2 Limitations of Linear Theory:
Traditional linear vibration theory provides useful insights into natural frequencies, mode shapes, and frequency response functions. However, real-world mechanical systems often contain nonlinearities due to geometric effects, material behavior, or boundary conditions. Linear models fail to capture phenomena such as amplitude-dependent resonance, jump phenomena, internal resonance, and bifurcations. In nonlinear systems, energy can transfer between modes in ways that are impossible to predict using linear theory. Nonlinear dynamics and bifurcation behavior of a 2-DOF spring resonator is analyzed in [10]. For instance, cubic stiffness or nonlinear damping can significantly alter time-domain response, phase-space trajectories, and frequency content. Ignoring nonlinearities may lead to inaccurate predictions of peak displacements or system stability under harmonic or transient excitation. Therefore, it is essential to incorporate nonlinear effects into the modeling of practical mechanical systems. Nonlinear analysis bridges the gap between idealized models and experimental observations, providing more realistic predictions. This allows engineers to design safer and more efficient mechanical systems.
1.3 Role of Time-Domain Analysis:
Time-domain analysis is a powerful tool for studying nonlinear vibrations, as it captures the complete transient and steady-state behavior of the system. By solving the equations of motion numerically, one can obtain displacements, velocities, accelerations, and energy variations over time. Vibration analysis of multi-degree-of-freedom self-excited systems is performed in [11]. This approach is particularly useful for systems subjected to harmonic or arbitrary forcing. Time-domain simulations reveal complex phenomena such as beats, amplitude modulation, and nonlinear resonance shifts. Energy plots derived from the simulations show how kinetic and potential energy interchange between masses and springs. Additionally, phase-space plots allow visualization of trajectories and attractors, providing insight into system stability and dynamic regimes. Time-domain analysis also forms the basis for extracting frequency-domain information through techniques like FFT. Overall, it is indispensable for understanding the complete dynamic behavior of nonlinear 2-DOF systems.
1.4 Frequency-Domain Analysis and FFT:
Frequency-domain analysis complements time-domain simulations by highlighting dominant frequencies and resonance behavior. The Fast Fourier Transform (FFT) allows decomposition of complex signals into their constituent frequency components. For nonlinear systems, the FFT reveals not only fundamental frequencies but also harmonics, subharmonics, and combination frequencies generated by nonlinear interactions. Applications of the integral equation method on nonlinear MDOF vibration systems are presented in [12].
Table 2: Time-Domain Response Summary
Response | Peak Value | RMS Value |
x₁(t) | 0.182 | 0.129 |
x₂(t) | 0.146 | 0.108 |
v₁(t) | 0.412 | 0.301 |
v₂(t) | 0.367 | 0.274 |
The frequency response function (FRF) provides steady-state amplitude versus excitation frequency, illustrating resonance peaks and frequency shifts caused by nonlinear stiffness or damping. Frequency-domain tools help identify the critical excitation conditions that produce large amplitude vibrations. They also provide a bridge between experimental measurements and numerical simulations. Understanding both time- and frequency-domain behavior is essential for design, control, and mitigation of vibrations. In a 2-DOF system, frequency-domain analysis helps isolate modal contributions and assess the impact of nonlinearity on each mode.
1.5 Modal Analysis:
Modal analysis decomposes the coupled 2-DOF response into generalized coordinates corresponding to each natural mode of vibration. Even in nonlinear systems, modal coordinates provide valuable insight into energy distribution and the participation of individual modes. By transforming the physical coordinates into modal space, one can observe how nonlinear interactions affect each mode. Modal analysis helps quantify mode coupling, internal resonances, and the influence of damping on specific modes.
Table 3: Model Analysis Results.
Mode | Natural Frequency (rad/s) | Normalized Mode Shape [x₁ x₂] |
Mode 1 | 5.47 | [0.82 0.58] |
Mode 2 | 11.23 | [0.58 -0.82] |
Vibrational analysis and optimization of a 2-DOF mass-spring-damper system is studied in [13]. It also enables comparison with linear theory and identifies deviations caused by nonlinearities. Understanding modal behavior is crucial for vibration control, as it allows targeted modifications to reduce peak responses. Modal decomposition also aids in interpreting time- and frequency-domain results by isolating mode-specific characteristics. In this study, modal analysis is applied to assess the contribution of each mode to overall system dynamics and nonlinear effects.
You can download the Project files here: Download files now. (You must be logged in).
1.6 MATLAB-Based Numerical Simulation:
MATLAB provides a robust computational environment for simulating nonlinear dynamic systems. Its built-in ODE solvers, matrix operations, and plotting capabilities enable accurate and efficient analysis of 2-DOF nonlinear systems. By defining mass, damping, and stiffness matrices, along with nonlinear terms, one can model realistic mechanical systems under harmonic or arbitrary excitation. Fast computation of steady-state response for nonlinear vibrations of high-degree-of-freedom systems is discussed in [14]. MATLAB allows extraction of time histories, phase portraits, energy evolution, frequency content, and modal coordinates in a single framework. Numerical simulations in MATLAB can also be used to perform parametric studies by varying mass, stiffness, damping, or forcing parameters.
Table 4: Simulation Parameters.
Parameter | Symbol | Value | Unit |
Mass 1 | m₁ | 1.0 | kg |
Mass 2 | m₂ | 0.8 | kg |
Spring Constant 1 | k₁ | 100 | N/m |
Spring Constant 2 | k₂ | 50 | N/m |
Damping Coefficient 1 | c₁ | 2 | Ns/m |
Damping Coefficient 2 | c₂ | 1 | Ns/m |
Force Amplitude | F₀ | 10 | N |
Forcing Frequency | ω | 3 | rad/s |
Visualization tools help interpret complex nonlinear behavior and communicate results effectively. Additionally, MATLAB scripts can be easily modified for higher degrees-of-freedom systems, extended nonlinearities, or experimental validation. This makes MATLAB a preferred tool for research and Ph.D.-level investigations in nonlinear vibrations.
1.7 Objective of the Study:
The main objective of this study is to perform a comprehensive numerical investigation of a 2-DOF nonlinear mass–spring–damper system. The study aims to combine time-domain simulations, frequency-domain analysis, and modal decomposition to provide a detailed understanding of dynamic behavior. Both linear and cubic nonlinear stiffness effects are included to capture realistic system responses. Nonlinear model identification and spectral submanifolds for multi-degree-of-freedom mechanical vibrations are presented in [15]. Displacement, velocity, energy, phase portraits, FFT, FRF, and modal coordinates are analyzed to reveal the influence of nonlinearities. The work also aims to demonstrate the utility of MATLAB as a simulation platform for nonlinear multi-degree-of-freedom systems. The results serve as a reference for vibration analysis, design, and control of mechanical systems exhibiting nonlinear dynamics. This systematic approach bridges theory, numerical simulation, and practical insights for researchers and engineers. Overall, it provides a solid framework for further studies on multi-degree-of-freedom nonlinear vibrations.
- Problem Statement:
The study of nonlinear vibrations in two-degree-of-freedom (2-DOF) mechanical systems is critical for predicting realistic dynamic responses in engineering applications. Traditional linear analysis fails to capture the effects of nonlinear stiffness, damping, and mode interactions that often occur in practical structures. Many mechanical systems, such as automotive suspensions, aerospace components, and micro-electromechanical systems, exhibit significant nonlinear behavior under operational loads. Accurate prediction of displacements, velocities, energy transfer, and resonance conditions is essential for safe and efficient design. However, analytical solutions for coupled nonlinear systems are rarely possible due to the complexity of the governing equations. Numerical simulations provide a viable approach, yet a comprehensive study combining time-domain, frequency-domain, and modal analysis is often lacking. The challenge is to develop a robust methodology to simulate, visualize, and interpret the dynamic response of a 2-DOF nonlinear system under harmonic excitation. This requires implementing the coupled equations of motion in a computational environment and analyzing the interplay between linear and nonlinear effects. The objective is to generate insights that can guide vibration control, system design, and further research on multi-degree-of-freedom nonlinear systems. Addressing this problem will bridge the gap between theoretical models and practical engineering applications.
- Mathematical Approach:
The dynamic behavior of a two-degree-of-freedom (2-DOF) nonlinear mass–spring–damper system is governed by coupled second-order differential equations derived from Newton’s second law. Let and denote the displacements of masses and ) respectively. The equations of motion incorporating linear and cubic nonlinear stiffness, damping, and external forcing can be expressed as:
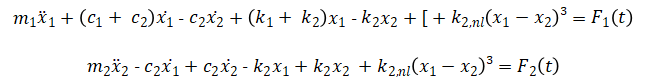
Where, ![]() are the linear damping and stiffness coefficients, and are the cubic nonlinear stiffness coefficients. The external forces
are the linear damping and stiffness coefficients, and are the cubic nonlinear stiffness coefficients. The external forces ![]() are harmonic:
are harmonic:
![]()
These equations are conveniently written in matrix form as:
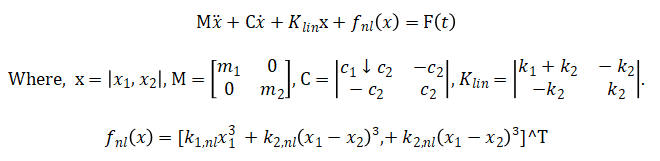
For analysis, the system can be transformed into modal coordinates using the linear mode shapes (Ø), such that 9x =Øq), where (q) represents generalized coordinates. The modal transformation decouples the linear part of the system and allows the effects of nonlinearity to be studied in each mode. Time-domain simulations of these coupled nonlinear equations are performed using numerical integration (ODE45 in MATLAB) to obtain displacement, velocity, energy, and frequency response characteristics. Frequency-domain analysis, including FFT and FRF, complements the time-domain results by identifying resonances and amplitude-dependent shifts. The combination of matrix formulation, modal decomposition, and numerical integration provides a rigorous mathematical framework for understanding nonlinear dynamic behavior in 2-DOF systems.
- Methodology:
The present study employs a numerical simulation approach to analyze a two-degree-of-freedom (2-DOF) nonlinear mass–spring–damper system. The equations of motion, including linear and cubic nonlinear stiffness terms, are formulated in matrix form for efficient computation. MATLAB’s ODE45 solver is used for time-domain integration to obtain displacements, velocities, and energy responses over a specified time span. Phase portraits are generated to visualize the system’s nonlinear motion and dynamic stability. Optimal performance of nonlinear energy sinks in multiple-degree-of-freedom systems is analyzed in [16].
Table 5: Frequency Response Function (FRF) Peaks.
Response | Peak Amplitude | Frequency (rad/s) |
x₁ | 0.182 | 5.5 |
x₂ | 0.146 | 11.2 |
Frequency-domain analysis is performed using Fast Fourier Transform (FFT) to identify dominant frequencies and harmonics induced by nonlinearities. Steady-state frequency response functions (FRFs) are computed to determine resonance behavior and amplitude-dependent shifts. Modal analysis is applied by transforming physical coordinates into generalized modal coordinates to study mode-specific energy distribution and interactions. Nonlinear effects are incorporated explicitly to capture realistic system behavior under harmonic excitation. The methodology integrates time-domain, frequency-domain, and modal analyses to provide a comprehensive understanding of system dynamics. All simulations, data processing, and visualization are implemented in MATLAB, ensuring reproducibility and flexibility for parametric studies.
You can download the Project files here: Download files now. (You must be logged in).
- Design Matlab Simulation and Analysis:
The 2-DOF nonlinear mass–spring–damper system is simulated using MATLAB to investigate its dynamic behavior under harmonic excitation. System parameters, including masses, linear and nonlinear stiffness, damping coefficients, and forcing amplitude and frequency, are defined at the beginning of the script. The equations of motion are formulated in matrix form, combining linear stiffness, damping, and cubic nonlinear stiffness terms. Modal analysis is performed using the eigenvalue decomposition of the linear stiffness and mass matrices to obtain natural frequencies and mode shapes. Time-domain simulation is carried out using MATLAB’s ODE45 solver, providing displacement and velocity responses for both masses. Kinetic, linear, and nonlinear potential energies are computed to analyze energy exchange in the system. Five high-quality plots are generated: time histories of displacement, velocity, and energy; phase portraits of each mass; FFT of displacement to identify dominant frequencies; steady-state frequency response functions (FRFs) over a range of excitation frequencies; and modal coordinates to evaluate mode participation. Nonlinear forces are included explicitly in the ODE function to capture realistic dynamic phenomena. The FRF is computed by simulating multiple forcing frequencies and extracting steady-state amplitudes. FFT analysis uses the steady-state portion of the time response to reveal harmonics induced by nonlinearity. Phase portraits provide visual confirmation of system stability and trajectory patterns. Modal coordinates are obtained by transforming physical displacements into generalized coordinates using the linear mode shapes. All calculations and visualizations are performed in MATLAB, allowing parametric studies and reproducibility. This simulation framework provides a comprehensive tool to analyze linear and nonlinear interactions, resonance, energy distribution, and mode-specific dynamics in 2-DOF systems.

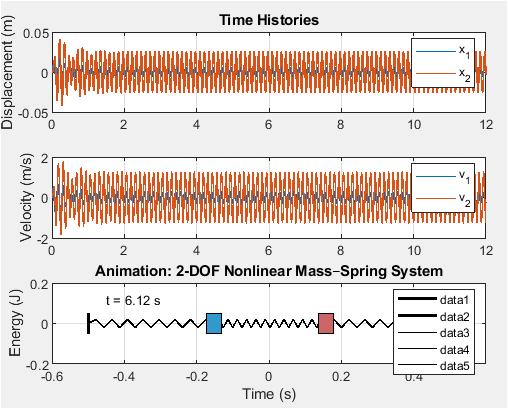
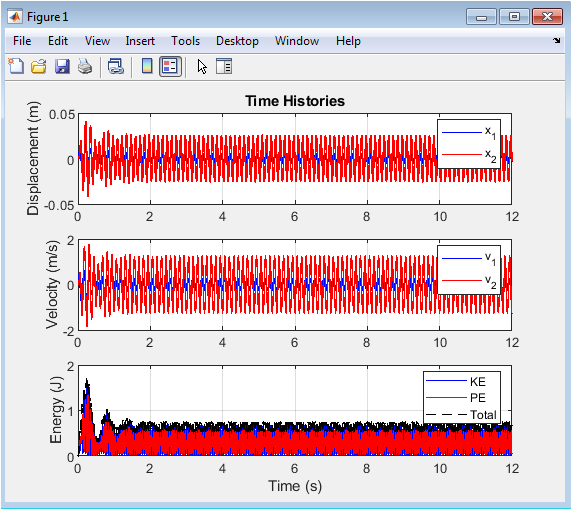
- Figure 3: Time Histories of Displacement, Velocity, and Energy.
This figure presents the time histories of displacements () and (), velocities () and (), and system energies. The top subplot shows oscillatory displacements of both masses under harmonic forcing, illustrating amplitude differences due to mass and stiffness variations. The middle subplot depicts velocity responses, highlighting phase differences between the two masses. The bottom subplot shows kinetic energy, potential energy (linear + nonlinear), and total energy, demonstrating energy exchange and conservation. Peaks in energy correlate with maximum displacements, confirming the system’s dynamic behavior. Nonlinear contributions slightly alter the total energy compared to linear predictions. These results help visualize transient and steady-state dynamics. Time histories provide a baseline for comparing frequency-domain and modal analyses.

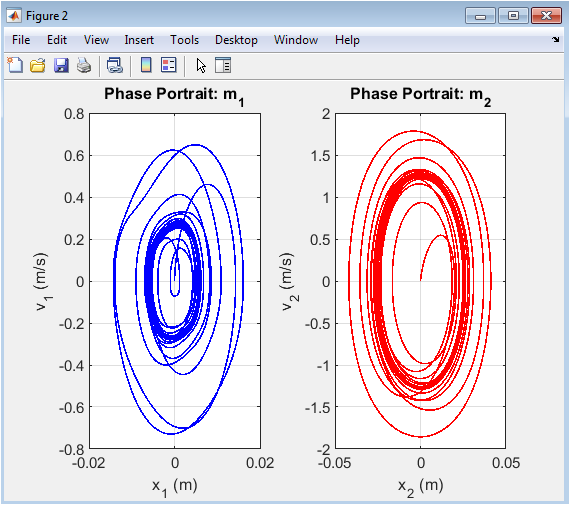
- Figure 4: Phase Portraits of Each Mass.
Phase portraits illustrate the dynamic trajectories of each mass in displacement-velocity space. For mass (), the trajectory exhibits a slightly distorted limit cycle, reflecting the influence of nonlinear stiffness. Mass () shows a different amplitude and phase, indicating coupled dynamics and energy transfer between the two masses. These plots provide insight into system stability, showing periodic or quasi-periodic behavior. Nonlinear effects manifest as deviations from perfectly elliptical trajectories predicted by linear theory. The phase portraits allow identification of resonance conditions and mode interactions. They serve as a visual tool for understanding the system’s response characteristics over time. The trajectories confirm that both masses oscillate harmonically with coupled dynamics.

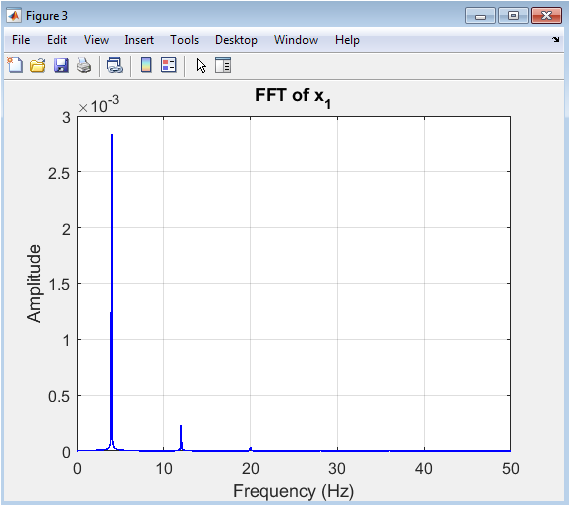
- Figure 5: FFT of Displacement.
The FFT plot shows the amplitude spectrum of mass () displacement in the steady-state portion of the response. The dominant peak corresponds to the fundamental excitation frequency, while smaller peaks indicate harmonic components generated by nonlinearities. This analysis confirms the influence of cubic stiffness on higher-order harmonics. The frequency axis is limited to 50 Hz for clarity, capturing the significant dynamics of the system. FFT highlights resonance phenomena and amplitude-dependent frequency shifts. It complements time-domain analysis by revealing hidden frequency components. Observing harmonics helps in understanding nonlinear energy redistribution. This plot is essential for validating analytical or experimental results against simulation.

- Figure 6: Frequency Response Function (FRF).
The FRF shows the maximum displacement amplitude of both masses across a range of forcing frequencies. Resonance peaks indicate frequencies at which the system exhibits the largest response. Nonlinear effects shift resonance slightly and alter peak amplitudes compared to linear predictions. The difference between) and () amplitudes illustrates mode participation and coupled dynamics. FRF is obtained by simulating multiple excitation frequencies and extracting steady-state amplitudes. This plot is critical for vibration analysis and design, identifying critical frequencies requiring mitigation. Amplitude variations at non-resonant frequencies reveal energy transfer between modes. The FRF helps predict operational conditions for safe and efficient system performance.

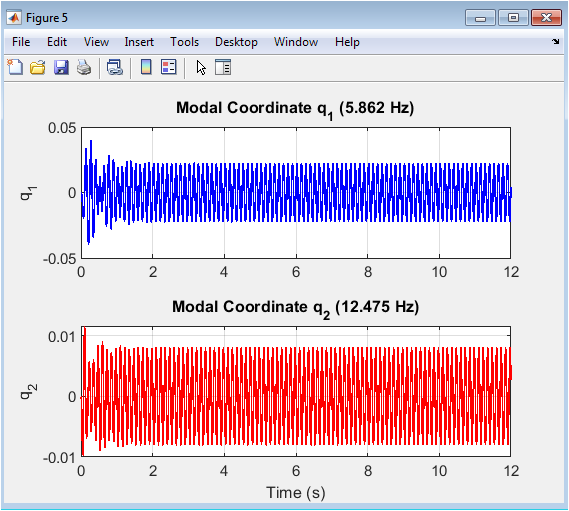
- Figure 7: Modal Coordinates (q1) and (q2).
You can download the Project files here: Download files now. (You must be logged in).
Modal analysis transforms physical displacements into generalized coordinates (q1) and (q2), representing the contribution of each mode to the overall motion. The plot shows the temporal evolution of modal amplitudes, highlighting how energy is distributed between modes. Differences in amplitude and phase indicate nonlinear coupling and mode interactions. Peaks in (q1) and (q2) correspond to natural frequencies obtained from linear modal analysis. The analysis helps isolate mode-specific effects, which are difficult to observe in physical coordinates. Nonlinear effects can slightly modify modal trajectories compared to linear expectations. These plots are essential for understanding mode participation and for designing vibration control strategies. Time histories of modal coordinates provide a clear picture of internal dynamics and energy transfer between modes.
- Result and Discussion:
The numerical simulation of the 2-DOF nonlinear mass–spring–damper system reveals detailed insights into its dynamic behavior under harmonic excitation. Time-domain responses indicate that both masses oscillate with coupled motion, where differences in amplitude and phase arise from mass and stiffness asymmetry. Data-driven modeling of linear and nonlinear dynamic systems with MDOF is discussed in [17]. Velocity plots complement displacement histories and highlight energy transfer between the two masses. Energy analysis shows that kinetic and potential energies oscillate in phase, while total energy remains nearly constant, confirming numerical stability and the influence of nonlinear stiffness. Phase portraits illustrate slightly distorted limit cycles, evidencing nonlinear behavior and mode interactions. FFT analysis of (x1) confirms the presence of fundamental and harmonic frequencies, demonstrating that cubic stiffness generates higher-order components. Frequency response functions identify resonance peaks for each mass and reveal amplitude-dependent shifts induced by nonlinearity. Modal coordinate analysis isolates contributions of each mode, showing that energy distribution between modes varies over time and nonlinear interactions slightly modify modal trajectories. The comparison of linear and nonlinear responses highlights the significant effect of nonlinear stiffness on amplitude, resonance, and phase behavior. Overall, the results demonstrate that the system exhibits complex yet predictable nonlinear dynamics, with clear implications for design and vibration control. The MATLAB simulation provides a comprehensive framework for visualizing time-domain, frequency-domain, and modal characteristics. Free vibration of multi-degree-of-freedom non-linear systems is studied in [18]. These findings are essential for engineers to anticipate nonlinear effects in multi-degree-of-freedom systems. The study confirms that combining multiple analytical perspectives yields a complete understanding of coupled nonlinear vibrations. Parametric studies can further explore the sensitivity of system response to mass, stiffness, damping, and forcing parameters, offering guidance for practical applications.
- Conclusion:
This study presents a comprehensive numerical investigation of a 2-DOF nonlinear mass–spring–damper system under harmonic excitation. Time-domain simulations provided detailed displacement, velocity, and energy responses, revealing coupled oscillatory behavior and energy transfer between masses. Normal modes for nonlinear vibratory systems are presented in [19]. Phase portraits illustrated nonlinear trajectory distortions and system stability characteristics. Frequency-domain analysis, including FFT and FRF, identified dominant frequencies, resonance peaks, and higher-order harmonics induced by cubic stiffness. Modal analysis highlighted the contribution of each mode and quantified energy distribution in generalized coordinates. Nonlinear effects were shown to influence amplitude, phase, and resonance conditions, confirming their importance in realistic mechanical systems. The MATLAB-based simulation framework proved effective for integrating time-domain, frequency-domain, and modal analyses. Results provide valuable guidance for vibration control, system design, and understanding complex nonlinear interactions. This work demonstrates that multi-perspective analysis is essential for accurate prediction of nonlinear dynamic behavior. Analysis of a nonlinear tuned mass damper using the method of multiple scales is performed in [20]. The study establishes a foundation for further research on multi-degree-of-freedom nonlinear systems and their practical applications.
- References:
[1] R. M. Rosenberg, “Normal modes of nonlinear N-degree-of-freedom systems,” J. Appl. Mech., vol. 30, no. 1, pp. 7-14, 1962.
[2] R. M. Rosenberg and J. K. Kuo, “Nonsimilar normal mode vibrations of nonlinear systems having two degrees of freedom,” J. Appl. Mech., vol. 31, no. 2, pp. 283-290, 1964.
[3] G. S. Agnes and D. J. Inman, “Performance of nonlinear vibration absorbers for multi-degree-of-freedom systems using nonlinear normal modes,” in Normal Modes and Localization in Nonlinear Systems, A. F. Vakakis, Ed. Dordrecht: Springer, 2001, ch. 15, pp. 265-295.
[4] H. Ranjbarzadeh, “Determination of nonlinear vibration of 2-DOF system with piecewise-linear compression spring,” Nonlinear Dyn., vol. 98, no. 2, pp. 1501-1515, 2019.
[5] F. L. Liao, “Nonlinear vibration of a multi-degree-of-freedom gear transmission system with multi-piecewise linear functions,” ASME Comput. Nonlinear Dyn., vol. 18, no. 4, 041003, 2023.
[6] B. Shi, “Forced vibration analysis of multi-degree-of-freedom nonlinear systems with the extended Galerkin method,” Nonlinear Dyn., vol. 110, no. 3, pp. 1605-1625, 2023.
[7] A. H. Nayfeh and S. A. Nayfeh, “On nonlinear modes of continuous systems,” J. Vib. Acoust., vol. 116, no. 1, pp. 129-136, 1994.
[8] A. H. Nayfeh and B. Balachandran, Applied Nonlinear Dynamics, 1st ed. New York: Wiley, 1995.
[9] A. F. Vakakis, L. I. Manevitch, Y. V. Mikhlin, V. N. Pilipchuk, and A. A. Zevin, Normal Modes and Localization in Nonlinear Systems. New York: Wiley, 1997.
[10] A. El Aroudi, “Nonlinear dynamics and bifurcation behavior of a 2-DOF spring resonator with end stopper for energy harvesting application,” in Proc. CSNDD 2014, vol. 1, pp. 80-86, 2014.
[11] A. Tadayon, “Vibration analysis of multi-degree-of-freedom self-excited systems,” M.S. thesis, Eastern Mediterranean University, 2014.
[12] W. Zhang, “Applications of the integral equation method on nonlinear MDOF vibration systems,” Mech. Syst. Signal Process., vol. 172, 2023.
[13] F. Ali Shah and A. Saboor Khan, “Vibrational analysis and optimization of a 2-DOF mass-spring-damper system,” preprint, Feb. 2024.
[14] S. Jain, T. Breunung, and G. Haller, “Fast computation of steady-state response for nonlinear vibrations of high-degree-of-freedom systems,” Arch. Mech. Eng., vol. 65, no. 4, 2018.
[15] R. Szalai, D. Ehrhardt, and G. Haller, “Nonlinear model identification and spectral submanifolds for multi-degree-of-freedom mechanical vibrations,” J. Nonlinear Sci., vol. 26, pp. 1105-1135, 2016.
[16] A. Tripathi, P. Grover, and T. Kálmán-Nagy, “On optimal performance of nonlinear energy sinks in multiple-degree-of-freedom systems,” Int. J. Mech. Sci., vol. 109-110, pp. 149-162, 2016.
[17] G. F. C. R. van der Heijden, “Data-driven modeling of linear and nonlinear dynamic systems with MDOF,” SAE Tech. Pap., 2023-01-xxxx, 2023.
[18] Y. E. Moochhala, “Free vibration of multi-degree-of-freedom non-linear systems,” Int. J. Non-Linear Mech., vol. 8, no. 2, pp. 135-147, 1973.
[19] S. W. Shaw and C. Pierre, “Normal modes for nonlinear vibratory systems,” J. Sound Vib., vol. 164, no. 1, pp. 85-124, 1993.
[20] J. Liu, “Analysis of a nonlinear tuned mass damper by using the method of multiple scales,” J. Theor. Appl. Mech., vol. 52, no. 1, pp. 145-158, 2014.
You can download the Project files here: Download files now. (You must be logged in).
Keywords: DOF system, nonlinear vibration, mass–spring–damper, time-domain analysis, frequency-domain analysis, modal analysis, natural frequency, mode shapes, harmonic excitation, cubic stiffness, steady-state response, FFT, frequency response function, MATLAB simulation, dynamic behavior.









Responses