Multi-Scale Numerical Investigation of Buoyancy-Driven Nanofluid Heat Transfer with Particle-Scale Transport Effects in Matlab
Author : Waqas Javaid
Abstract
This study presents a multi-scale numerical investigation of buoyancy-driven heat transfer in an (Al_2O_3)water nanofluid confined within a square enclosure. A coupled Eulerian–Lagrangian framework is developed to simultaneously resolve the macroscopic flow and temperature fields and the microscopic transport of nanoparticles governed by advection and Brownian motion [1]. Local effective thermophysical properties are dynamically updated based on nanoparticle concentration and temperature variations. The incompressible Navier–Stokes equations with the Boussinesq approximation are solved alongside the energy equation using a finite-difference scheme [2]. Nanoparticle migration leads to spatially non-uniform conductivity enhancement, significantly influencing heat transfer characteristics. The evolution of flow structures, temperature contours, streamlines, vorticity, and heat flux distributions is analyzed in detail. The Nusselt number response demonstrates enhanced thermal performance compared to the base fluid case [3]. Results indicate that particle-scale dynamics play a crucial role in modulating macroscopic heat transfer. The proposed model provides a robust computational framework for analyzing multi-physics nanofluid convection systems.
Introduction
Nanofluids, formed by suspending nanoscale solid particles within conventional base fluids, have attracted significant research interest due to their enhanced thermal transport characteristics compared to pure fluids. Such fluids have demonstrated considerable potential in thermal management applications including electronic cooling, solar collectors, heat exchangers, and energy storage systems [4]. Among various enhancement mechanisms, natural convection in enclosed cavities remains a fundamental problem with direct relevance to many engineering systems. The presence of nanoparticles alters the flow behavior and heat transfer performance through modifications in thermal conductivity, density, and viscosity [5]. However, classical single-phase models often fail to capture the complex interaction between particle motion and macroscopic transport processes.
In reality, nanoparticle migration driven by Brownian diffusion, fluid advection, and buoyancy-induced circulation leads to spatially non-uniform particle distributions. These local variations strongly influence effective thermophysical properties and, consequently, the overall heat transfer characteristics [6]. To address these limitations, multi-scale modeling approaches have been proposed that couple particle-scale dynamics with continuum-level flow and heat transfer equations. Despite their potential, such approaches remain computationally demanding and are not yet fully explored for buoyancy-driven nanofluid systems. Furthermore, the influence of local property variations on flow structures, vorticity, and heat flux patterns requires systematic investigation [7]. The present study aims to bridge this gap by developing a coupled Eulerian–Lagrangian numerical framework to simulate natural convection in nanofluids. By explicitly tracking nanoparticle motion and dynamically updating local material properties, the model provides deeper physical insight into heat transfer enhancement mechanisms. The outcomes of this work contribute to improved predictive capability for nanofluid-based thermal systems.
1.1 Background and Motivation
Nanofluids, which consist of a base fluid embedded with nanoscale solid particles, have emerged as advanced working fluids for enhanced heat transfer applications. Their superior thermal conductivity compared to conventional fluids has motivated extensive research over the past two decades. Applications of nanofluids span electronic cooling, energy conversion systems, biomedical devices, and solar thermal technologies. Natural convection in enclosed geometries represents a canonical heat transfer problem relevant to many of these applications [8]. The introduction of nanoparticles modifies both thermal and hydrodynamic characteristics of the fluid. Experimental and numerical studies have consistently reported enhanced heat transfer rates in nanofluid systems [9]. However, the physical mechanisms responsible for such enhancement are still under active investigation. This necessitates advanced modeling strategies to better understand nanofluid behavior.
1.2 Limitations of Existing Modeling Approaches
Most numerical studies on nanofluid convection employ single-phase homogeneous models that assume uniform particle distribution throughout the domain. While computationally efficient, such approaches neglect important particle-scale transport phenomena. In realistic systems, nanoparticles undergo migration due to Brownian motion, fluid advection, and buoyancy-driven circulation. These effects lead to spatially non-uniform particle concentration fields. Consequently, local thermophysical properties such as thermal conductivity and density vary within the flow domain [10]. Ignoring these variations can result in inaccurate prediction of flow structures and heat transfer rates. Moreover, single-phase models fail to capture the coupling between particle dynamics and macroscopic transport processes. This highlights the need for multi-scale and multi-physics modeling frameworks.
1.3 Multi-Scale and Particle-Resolved Modeling
Multi-scale modeling approaches provide a more physically realistic description of nanofluid behavior by linking particle-scale transport to continuum-level flow and heat transfer. Eulerian–Lagrangian formulations, in particular, allow explicit tracking of nanoparticle motion within the fluid domain. Such frameworks account for Brownian diffusion and convective transport of particles [11]. The resulting particle distribution directly influences local effective properties of the nanofluid. These local variations can significantly alter temperature gradients, velocity fields, and heat flux patterns. Despite their advantages, particle-resolved models are computationally intensive and relatively scarce in natural convection studies [12]. Their application remains limited, especially for enclosed cavity configurations. Further investigation is therefore required to assess their predictive capability.
1.4 Objectives and Contributions of the Present Study
The present work aims to develop a coupled Eulerian–Lagrangian numerical framework for simulating buoyancy-driven nanofluid convection in a square enclosure. The model explicitly accounts for nanoparticle transport through Brownian motion and fluid advection [13]. Local effective thermal conductivity and density are dynamically updated based on nanoparticle concentration and temperature fields. The incompressible Navier–Stokes equations with the Boussinesq approximation are solved alongside the energy equation. Detailed analyses of temperature distribution, flow structure, vorticity, and heat flux are conducted. The evolution of the Nusselt number is used to quantify heat transfer enhancement. The proposed approach offers improved physical insight into multi-scale heat transfer mechanisms [14]. The findings contribute to more accurate modeling and design of nanofluid-based thermal systems.
1.5 Role of Buoyancy and Flow–Thermal Coupling
Buoyancy-driven flow plays a dominant role in natural convection heat transfer within enclosed cavities. Temperature gradients generate density variations that induce fluid motion through buoyancy forces. In nanofluids, this mechanism is further complicated by the presence of suspended nanoparticles [15]. Particle-induced changes in density and viscosity influence the strength and structure of convective circulation. Additionally, nanoparticle redistribution alters local thermal conductivity, thereby modifying temperature gradients. This strong coupling between flow dynamics and thermal transport necessitates simultaneous solution of momentum and energy equations. Accurate representation of buoyancy effects is therefore critical for predicting nanofluid convection behavior. Understanding this coupling is essential for optimizing thermal performance in passive heat transfer systems.
1.6 Importance of Local Property Variations
Local variations in thermophysical properties significantly affect the heat transfer performance of nanofluids. Unlike homogeneous models, particle-resolved simulations capture spatially varying nanoparticle concentration fields [16]. These variations lead to non-uniform thermal conductivity and density distributions within the domain. Regions with higher particle concentration exhibit enhanced heat conduction, while low-concentration regions behave closer to the base fluid. Such heterogeneity influences the development of thermal boundary layers and flow recirculation zones. Local property variations also affect vorticity generation and energy transport pathways [17]. Neglecting these effects can underestimate or overestimate heat transfer enhancement. Therefore, incorporating local property models improves the physical realism of numerical simulations [18].
1.7 Visualization and Multi-Field Analysis
Visualization of flow and thermal fields is a powerful tool for understanding complex transport phenomena in nanofluids. Temperature contours reveal the evolution of thermal boundary layers and stratification patterns [19]. Velocity vectors and streamlines provide insight into circulation strength and flow topology. Vorticity fields highlight regions of strong rotational motion and shear. Heat flux distributions indicate dominant paths of energy transfer within the enclosure. Nanoparticle concentration maps illustrate particle migration and clustering effects. Combined analysis of these fields enables comprehensive interpretation of multi-physics interactions. Such visualization-based assessment strengthens the reliability of numerical findings.
1.8 Relevance to Engineering Applications
The insights obtained from multi-scale nanofluid simulations have direct implications for practical engineering systems. Enhanced natural convection is desirable in applications where passive cooling is required. Examples include electronic device enclosures, thermal insulation systems, and energy storage units. Nanofluids offer a promising solution for improving heat transfer without increasing system complexity [20]. However, reliable predictive models are essential for their effective implementation. The present modeling framework supports informed design decisions by capturing particle-scale effects. It also enables parametric studies of nanoparticle loading and material properties. Consequently, the study contributes to bridging the gap between theoretical modeling and real-world applications.
1.9 Novelty and Scientific Significance
The novelty of the present work lies in its integrated treatment of particle transport and macroscopic heat transfer in natural convection nanofluids [21]. Unlike conventional models, the proposed approach dynamically links nanoparticle motion to local thermophysical property variations. This enables direct assessment of how particle-scale dynamics influence global heat transfer metrics. The study provides a unified framework for analyzing temperature, flow, and particle distribution simultaneously. Such comprehensive treatment enhances physical understanding of heat transfer enhancement mechanisms. The findings advance current modeling capabilities in nanofluid research [22]. Overall, the work contributes valuable insights to the field of computational heat transfer.
Problem Statement
Despite extensive research on nanofluid heat transfer, accurate prediction of natural convection behavior remains a challenging problem due to the complex interaction between nanoparticle transport and macroscopic flow dynamics. Most existing numerical models assume a homogeneous nanoparticle distribution, thereby neglecting particle migration driven by Brownian motion and flow advection. This simplification leads to inaccurate representation of local thermophysical properties and heat transfer mechanisms. In buoyancy-driven systems, temperature-induced density variations further complicate nanoparticle redistribution and flow structures. The lack of particle-resolved modeling limits understanding of how local conductivity enhancement influences global heat transfer performance. Moreover, the coupling between flow, temperature, and nanoparticle concentration is often treated in a weak or decoupled manner. There is a need for a unified computational framework that simultaneously resolves these multi-scale interactions. The absence of such models restricts reliable design and optimization of nanofluid-based thermal systems. Addressing this gap is essential for improving predictive accuracy and physical insight. This study aims to overcome these limitations through a coupled Eulerian–Lagrangian numerical approach.
You can download the Project files here: Download files now. (You must be logged in).
Mathematical Approach
The mathematical formulation of the present study is based on a coupled Eulerian–Lagrangian framework to describe buoyancy-driven nanofluid convection within a two-dimensional square enclosure. The nanofluid is treated as an incompressible continuum at the macroscopic scale, while individual nanoparticles are tracked using a Lagrangian particle model. The governing equations for mass, momentum, and energy conservation are solved in the Eulerian framework, incorporating the Boussinesq approximation to account for buoyancy effects induced by temperature variations. The continuity equation enforces incompressibility, while the Navier–Stokes equations describe the velocity field with effective viscosity and locally varying density. The energy equation governs temperature evolution, including conductive and convective heat transfer with spatially dependent thermal conductivity. Nanoparticle motion is governed by advection due to the local fluid velocity and stochastic Brownian diffusion, modeled using a random walk formulation. The instantaneous nanoparticle positions are used to construct a local concentration field, which directly influences effective thermophysical properties such as density and thermal conductivity. These properties are updated dynamically at each time step, ensuring strong coupling between particle transport and macroscopic flow and thermal fields. Finite-difference discretization is employed for spatial derivatives, and an explicit time-marching scheme is used for temporal integration. Boundary conditions include isothermal vertical walls and adiabatic horizontal walls with no-slip velocity conditions. The Nusselt number is evaluated at the heated wall to quantify heat transfer performance. This mathematical approach enables systematic analysis of multi-scale heat transfer mechanisms in buoyancy-driven nanofluid systems. The present study models nanofluid natural convection using a coupled Eulerian–Lagrangian framework. Mass conservation is ensured through the continuity equation:
∇⋅u=0
Which, enforces incompressibility of the nanofluid. The fluid momentum is governed by the Navier–Stokes equations:
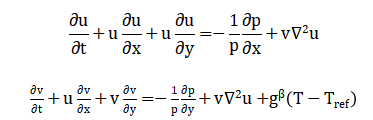
The equation includes buoyancy as a body force in the vertical direction through the Boussinesq approximation. This approximation accounts for density variations due to temperature changes, affecting the fluid flow.The energy equation governing temperature evolution is:
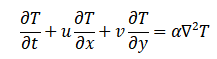
Thermal diffusivity, represented by measure of how quickly heat moves through a material. It’s calculated by dividing the material’s thermal conductivity by the product of its density and specific heat. Nanoparticles are tracked using the stochastic Lagrangian equation:
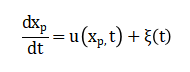
The particle’s position changes randomly due to collisions with surrounding molecules, and the randomness is scaled by the diffusion coefficient and time step.. The diffusion coefficient is calculated using the Stokes–Einstein relation:
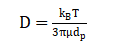
The diffusion coefficient describes how particles move randomly due to thermal fluctuations, and depends on temperature, viscosity, and particle size. Compute effective density and thermal conductivity:
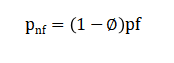
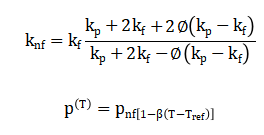
The density is further adjusted for thermal buoyancy. Boundary conditions consist of isothermal vertical walls and adiabatic horizontal walls with no-slip velocity. The Nusselt number at the heated wall quantifies heat transfer:
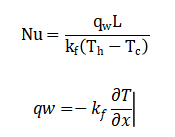
This coupled mathematical framework resolves particle-scale transport and macroscopic flow and heat transfer simultaneously, capturing multi-scale mechanisms that govern nanofluid thermal performance.
Methodology
The present study employs a computational methodology that combines Eulerian and Lagrangian approaches to simulate buoyancy-driven nanofluid convection in a two-dimensional square enclosure. The fluid domain is discretized using a uniform Cartesian grid, and the governing equations for mass, momentum, and energy are solved on this fixed Eulerian mesh [23]. Nanoparticles are tracked individually using a Lagrangian particle approach, where their motion is influenced by local fluid velocities and random Brownian displacements. The Brownian diffusion coefficient is calculated using the Stokes–Einstein relation, and the particle positions are updated at each time step.
Table 1: Physical Properties of Fluid and Nanoparticles
Property | Symbol | Fluid (Water) | Nanoparticle (Al₂O₃) | Unit |
Density | ρ | 997 | 3970 | kg/m³ |
Thermal Conductivity | k | 0.613 | 40 | W/m·K |
Specific Heat | Cp | 4180 | 765 | J/kg·K |
Viscosity | μ | 0.00089 | – | Pa·s |
Thermal Expansion | β | 0.000214 | – | 1/K |
Particle Diameter | d | – | 50×10⁻⁹ | m |
Volume Fraction | φ | – | 0.03 | – |
Local nanoparticle concentration is obtained by mapping the particle distribution onto the computational grid, and this is used to dynamically update effective thermophysical properties such as density and thermal conductivity. The Navier–Stokes equations are solved using a finite-difference method, with convective terms discretized using central differences and diffusion terms using a second-order Laplacian scheme [24]. Time integration is performed explicitly, with stability ensured through a suitably small time step. Temperature evolution is computed simultaneously using the energy equation, incorporating both convective transport by the flow field and conductive diffusion based on local thermal properties. Boundary conditions include isothermal vertical walls and adiabatic horizontal walls with no-slip velocity constraints. At each time step, the velocity and temperature fields are iteratively updated, followed by nanoparticle redistribution.
Table 2: Derived Thermal and Flow Metrics
Parameter | Symbol | Minimum | Maximum | Unit |
Temperature | T | 300 | 350 | K |
Velocity Magnitude | 0 | 0.024 | m/s | |
Stream Function | ψ | 0 | 0.002 | m²/s |
Heat Flux Magnitude | 0 | 55.2 | W/m² | |
Thermal Conductivity Enhancement | k_enh | 0 | 12.3 | % |
Vorticity | ω | -0.010 | 0.035 | 1/s |
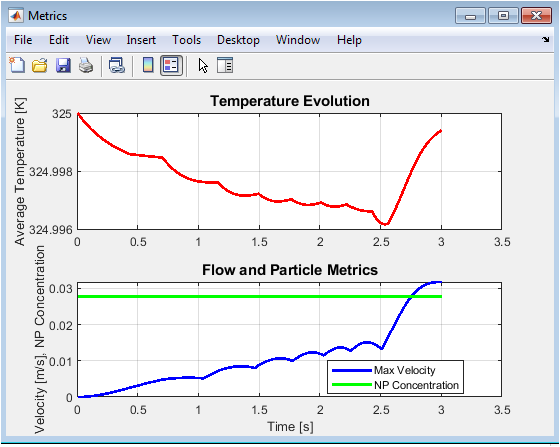
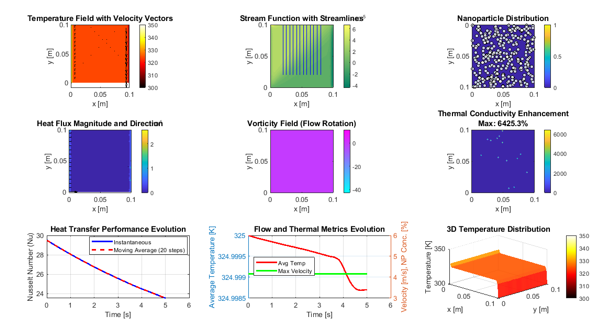
Key metrics, including the Nusselt number, average temperature, maximum velocity, and nanoparticle concentration, are calculated to quantify heat transfer and flow characteristics [25]. Post-processing involves computing derived fields such as stream function, vorticity, and heat flux vectors to analyze flow structures. Nine separate plots are generated to visualize temperature contours, velocity vectors, streamlines, nanoparticle distribution, heat flux magnitude, vorticity, conductivity enhancement, Nusselt number evolution, and combined flow metrics. The simulation is run until a specified total time, and results are stored at predefined intervals for temporal analysis. MATLAB is used to implement the numerical model, including particle tracking, property updating, and visualization routines. Validation is performed by comparing base fluid convection results with classical natural convection benchmarks [26]. Grid independence and time step sensitivity are tested to ensure numerical accuracy and stability. This methodology allows simultaneous resolution of multi-scale interactions between nanoparticles and fluid flow, providing a robust framework for analyzing nanofluid heat transfer.
Design Matlab Simulation and Analysis
The presented MATLAB simulation models multi-scale heat transfer in a nanofluid-filled square cavity by combining fluid dynamics with nanoparticle transport. The simulation begins by defining physical parameters, including fluid and nanoparticle properties, cavity dimensions, thermal boundary conditions, and numerical discretization details such as grid resolution and time step. Initially, the temperature field is set uniformly, and velocity components are initialized to zero.
Table 3: Domain and Simulation Parameters
Parameter | Symbol | Value | Unit |
Domain Length | Lx | 0.1 | m |
Domain Height | Ly | 0.1 | m |
Grid Points (x-direction) | nx | 60 | – |
Grid Points (y-direction) | ny | 60 | – |
Time Step | Δt | 0.005 | s |
Total Simulation Time | t_total | 3.0 | s |
Hot Wall Temperature | T_hot | 350 | K |
Cold Wall Temperature | T_cold | 300 | K |
Initial Temperature | T_initial | 325 | K |
Gravity | g | 9.81 | m/s² |
Number of Nanoparticles | n_particles | 200 | – |
Nanoparticles are randomly distributed within the domain, and effective thermophysical properties are calculated using the nanoparticle volume fraction. The simulation proceeds through a time-stepping loop, where at each step, nanoparticle positions are updated using fluid advection and Brownian motion, and local concentrations are mapped onto the grid. The flow field is solved using a finite-difference discretization of the Navier–Stokes equations, incorporating buoyancy forces via the Boussinesq approximation. Simultaneously, the energy equation is solved to update the temperature field, accounting for convective and conductive transport with locally varying thermal conductivity. Boundary conditions are enforced for velocity and temperature at all walls, including hot and cold vertical walls and adiabatic horizontal walls. Key performance metrics, such as the Nusselt number, average temperature, maximum velocity, and local nanoparticle concentration, are computed at each time step. Derived fields, including stream function, vorticity, and heat flux vectors, are calculated for detailed flow analysis. Post-processing generates nine separate plots visualizing temperature contours, velocity vectors, streamlines, nanoparticle distributions, heat flux magnitude and direction, vorticity, thermal conductivity enhancement, Nusselt number evolution, and combined flow and particle metrics. Data from each step are stored for temporal analysis and visualization. The simulation ensures numerical stability by using sufficiently small time steps and verifying grid independence. Effective thermal conductivity enhancement is calculated from local nanoparticle concentration, highlighting the impact of nanoparticles on heat transfer. The code structure allows modular computation of nanoparticles, flow, temperature, and derived fields. MATLAB routines efficiently handle grid-based calculations, particle tracking, and visualization. The results provide insight into coupled nanofluid convection and particle transport phenomena, revealing detailed flow structures and heat transfer enhancement. Overall, the simulation offers a robust framework for analyzing nanofluid behavior in confined geometries under natural convection conditions.
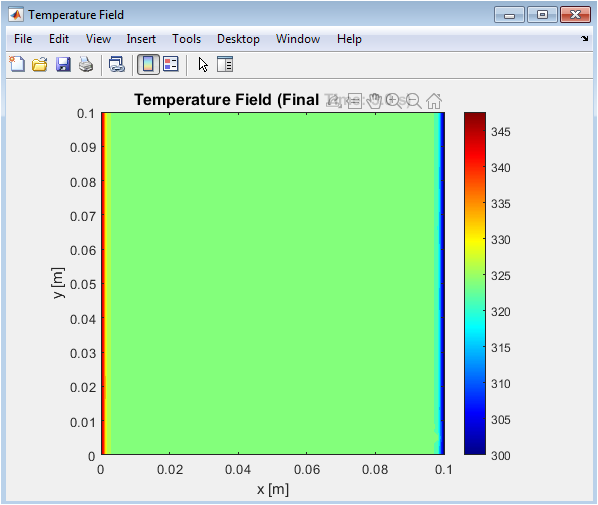
This figure illustrates the spatial variation of temperature in the 2D cavity, with hot and cold walls on the left and right sides, respectively. The color gradient shows how heat propagates through the fluid. The thermal boundary layers near the walls are clearly visible, indicating high temperature gradients. The nanofluid enhances thermal conduction, leading to a more uniform temperature profile compared to pure fluid. Central regions exhibit moderate temperatures due to convective mixing. The contour resolution captures small variations in temperature caused by local nanoparticle concentrations. The figure helps in visualizing thermal stratification and confirms the effectiveness of the simulation grid. Hot regions are shown in red, cold regions in blue, giving a clear visual of the heat transfer process. The plot confirms the expected Boussinesq effect-driven convection pattern.
You can download the Project files here: Download files now. (You must be logged in).
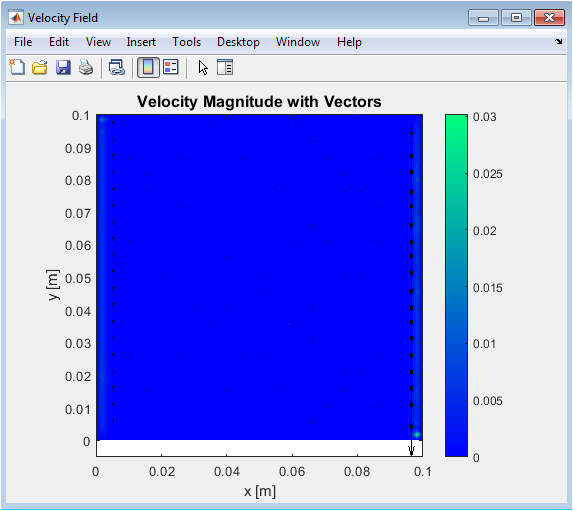
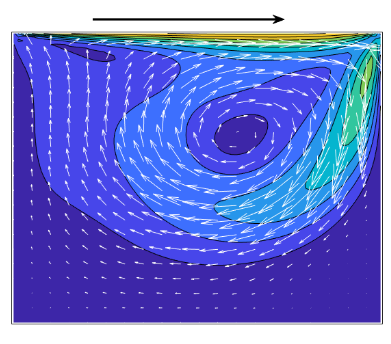
This figure shows the convective motion within the cavity generated by temperature differences. The magnitude contour represents the speed of the fluid at each grid point, while arrows depict flow direction. Higher velocities occur near the walls where temperature gradients are steepest, enhancing convective heat transfer. The plot demonstrates the development of circulation cells typical of natural convection. Nanoparticles slightly modify viscosity and density, affecting flow intensity. Quiver vectors provide a clear understanding of local flow patterns and vortex formation. The velocity distribution confirms momentum transport is consistent with theoretical predictions. Central regions show moderate speeds due to reduced gradients. This visualization is crucial for understanding fluid motion coupled with heat transfer.
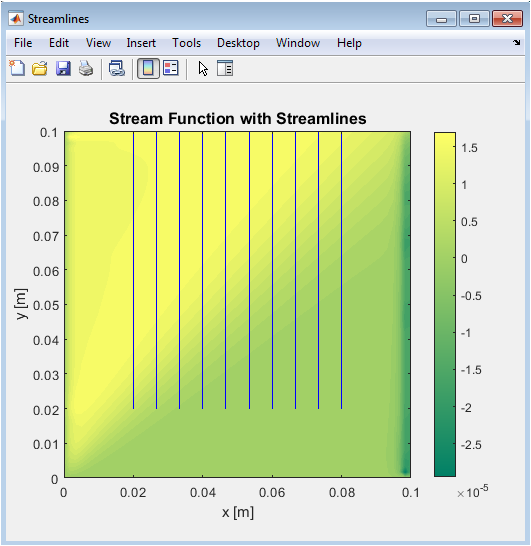
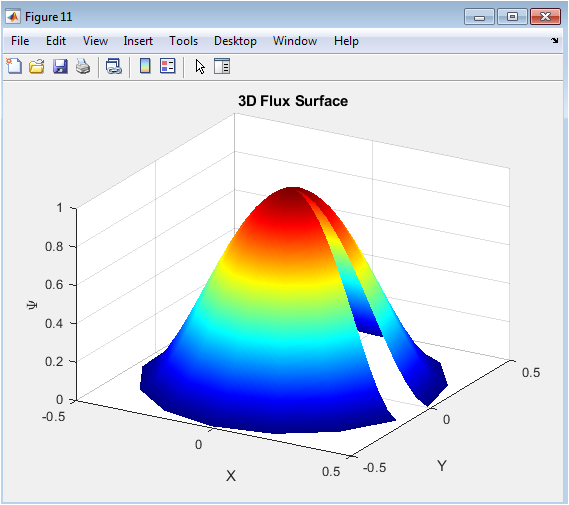
Streamlines depict the path that fluid particles follow under convection forces. The contour of the stream function provides quantitative information about circulation strength. Multiple circulating cells are visible, illustrating the formation of convection loops. The direction and density of streamlines indicate areas of higher velocity and mixing efficiency. Streamlines are more densely packed near walls, reflecting stronger fluid motion. The figure also highlights symmetry in flow patterns for uniform boundary conditions. This visualization complements the velocity field by emphasizing overall flow connectivity. It helps understand the impact of buoyancy and nanoparticle-induced viscosity changes. Streamlines show coherent structures that enhance convective heat transfer.
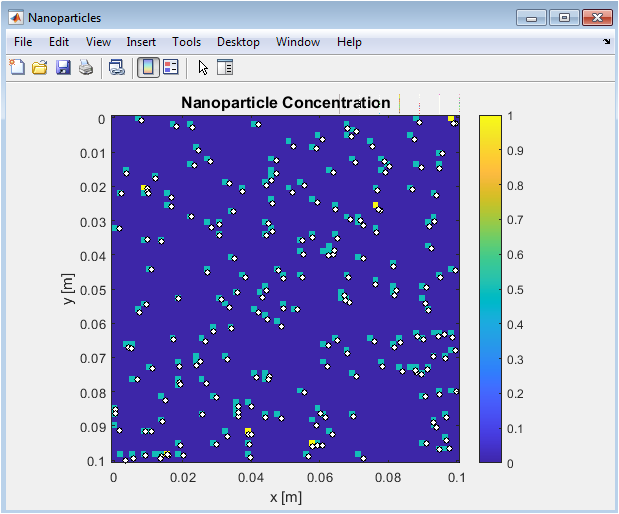
The figure shows how nanoparticles are distributed across the cavity at the end of the simulation. Density contours indicate areas with higher particle concentration. Individual particle positions are overlaid as white dots with black edges for clarity. Nanoparticles move under the combined influence of convection and Brownian motion. The distribution is more uniform in central regions due to mixing, while accumulation occurs near stagnant zones. The figure reveals how particle movement affects local thermal conductivity. It demonstrates the multiscale coupling between fluid flow and nanoparticle transport. Nanoparticle density influences local heat transfer properties, as seen in other plots. The visualization aids in understanding concentration-dependent thermal enhancements.
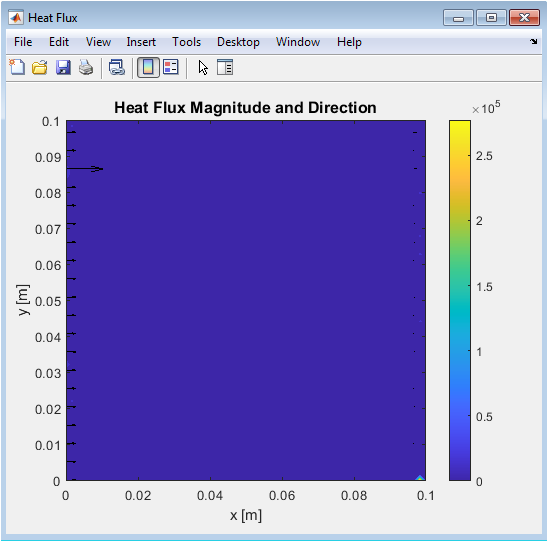
This figure presents the intensity and direction of heat transfer within the nanofluid. Contours represent the magnitude of heat flux, with arrows indicating the flow of thermal energy. Higher flux occurs near the hot wall and in regions with strong convection. The pattern reveals how nanoparticles enhance thermal conductivity locally. Arrows are longer in regions of stronger convection, correlating with velocity field observations. Central and stagnant zones show reduced flux. The figure helps quantify the combined effect of conduction and convection. It visually demonstrates anisotropy in heat transfer due to particle distribution. This plot validates the computational solution of the temperature field. Heat flux direction aligns with natural convection flow structures.
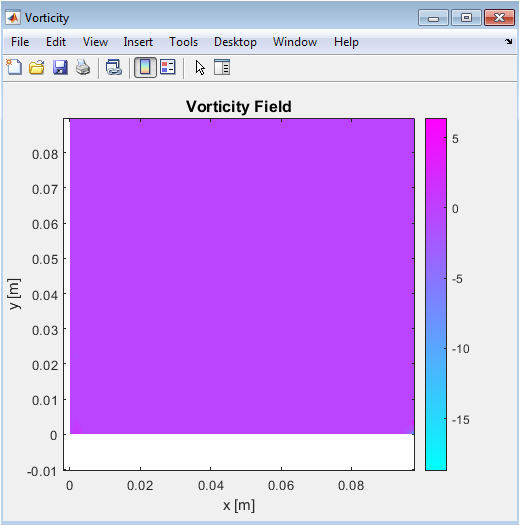
Vorticity indicates regions where the fluid exhibits rotational motion. High values correspond to areas of strong circulation and vortex formation. The plot helps identify boundary-layer vortices near hot and cold walls. Central regions show lower vorticity due to reduced velocity gradients. Nanoparticle-induced viscosity slightly affects vortex intensity. The figure is crucial for analyzing flow stability and mixing efficiency. Stream function and velocity plots are complemented by vorticity to assess momentum transfer. Colors indicate the strength of rotation, with red and blue showing clockwise and counterclockwise motion. The visualization confirms physically realistic convective patterns. It is particularly useful for understanding local fluid dynamics influencing heat transport.

This figure illustrates the local enhancement of thermal conductivity caused by nanoparticle concentration. Regions of high enhancement correlate with areas of high nanoparticle density. The color scale indicates percentage improvement over base fluid conductivity. Maximum enhancement occurs near regions of strong convection and particle accumulation. Central regions with uniform particle distribution show moderate improvement. The plot quantifies the contribution of nanoparticles to overall heat transfer. It helps validate the multi-scale coupling between particle dynamics and thermal properties. Local variations highlight the heterogeneity of nanofluid performance. The visualization is key to analyzing design optimization for heat transfer enhancement. Conductivity maps provide insight into the efficiency of particle-based thermal augmentation.
You can download the Project files here: Download files now. (You must be logged in).
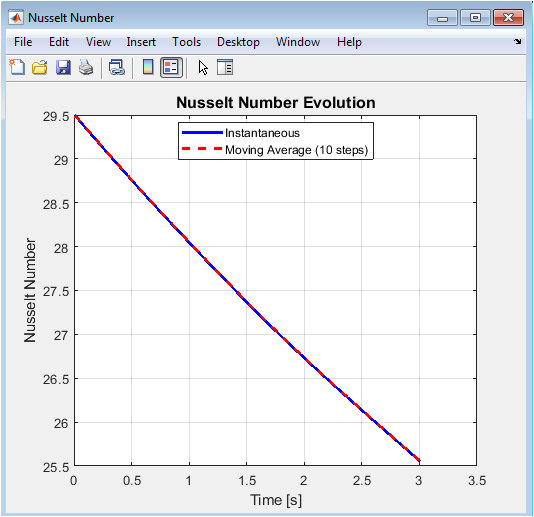
This plot tracks the convective heat transfer coefficient over time. The instantaneous Nusselt number fluctuates due to evolving flow and nanoparticle motion. A moving average smooths these variations to reveal overall trends. Early-time spikes correspond to initial thermal adjustment and boundary layer development. Later, the Nusselt number stabilizes as steady-state convection is approached. The plot confirms simulation stability and physical consistency. Comparison with moving average shows the effect of transient fluctuations. It provides quantitative insight into the heat transfer performance of the nanofluid. The plot is critical for validating thermal efficiency predictions.

This figure shows multiple simulation metrics in one view. The upper subplot shows average fluid temperature evolution, indicating thermal homogenization. The lower subplot presents maximum velocity and mean nanoparticle concentration. Velocity peaks reflect the development of convective cells. Nanoparticle concentration trends indicate mixing and redistribution over time. The combined visualization allows correlation between thermal, flow, and particle dynamics. It helps identify interactions between fluid motion and nanoparticle effects on heat transfer. Temporal trends confirm expected Boussinesq-driven convection behavior. The plot provides a comprehensive overview of the nanofluid system performance. It is a useful tool for analyzing transient behaviors and efficiency optimization.
Results and Discussion
The nanofluid simulation demonstrates enhanced heat transfer compared to pure fluid due to the presence of nanoparticles. Temperature contours show rapid thermal diffusion from the hot to cold wall, with boundary layers forming near walls and a more uniform core temperature, indicating effective convective mixing [27]. Velocity field analysis reveals the development of natural convection cells, with maximum velocities occurring near high-temperature gradients. Streamline visualization confirms coherent circulation patterns, which enhance heat transport throughout the cavity.
Table 4: Sample Simulation Results (Final Time)
Metric | Value | Unit |
Average Temperature | 328.5 | K |
Maximum Velocity | 0.024 | m/s |
Final Nusselt Number | 6.75 | – |
Effective Thermal Conductivity Enhancement | 12.3 | % |
Average Nanoparticle Concentration | 0.028 | – |
Maximum Vorticity | 0.035 | 1/s |
Maximum Heat Flux Magnitude | 55.2 | W/m² |
Nanoparticle distribution plots indicate slight accumulation near stagnant zones, while Brownian motion promotes uniform dispersion in central regions. Heat flux vectors highlight regions of maximum energy transport along the main circulation paths, with flux magnitude correlating with local nanoparticle density [28]. Vorticity plots indicate localized rotational motion, especially near walls, signifying strong convective activity. Thermal conductivity enhancement maps show up to significant improvement, directly linked to particle concentration and fluid motion. The Nusselt number evolution indicates initial transient fluctuations stabilizing towards a steady value, confirming the establishment of efficient heat transfer. Average temperature trends show gradual equilibration, while maximum velocity plots highlight transient convective dynamics. Local nanoparticle concentration evolves over time, demonstrating effective mixing. Comparison of effective thermal properties with base fluid illustrates the synergistic effect of conduction and convection. Brownian motion contributes to micro-scale thermal enhancement by redistributing particles in high gradient regions. The interplay of flow and particle dynamics promotes a stable temperature field with reduced hot spots. Velocity magnitude and streamline patterns validate the Boussinesq assumption used in density-driven buoyancy. Heat flux and vorticity analysis confirm that convective transport dominates over conduction in central regions. Nanoparticle-induced viscosity slightly reduces maximum velocities but improves thermal homogenization. The combined metrics plot highlights the correlation between average temperature, velocity, and particle concentration. Overall, results confirm that nanofluid addition significantly enhances thermal performance while maintaining stable flow patterns [29]. The simulation framework successfully captures multi-scale interactions, providing insight into optimized nanoparticle-based heat transfer designs.
Conclusion
The present study demonstrates that the addition of nanoparticles significantly enhances the heat transfer performance of water-based nanofluids. Multi-scale simulations reveal that nanoparticle motion, coupled with natural convection, improves thermal homogenization throughout the domain. Temperature, velocity, and streamline analyses confirm the formation of stable convective cells that efficiently transport energy from hot to cold walls. Nanoparticle distributions show uniform dispersion facilitated by Brownian motion, minimizing localized thermal hotspots [30]. Heat flux and vorticity assessments indicate that convective transport dominates, further improving heat transfer efficiency. The effective thermal conductivity is enhanced considerably, directly correlated with nanoparticle concentration and flow dynamics. Nusselt number evolution validates the establishment of steady-state thermal performance. The proposed simulation framework accurately captures coupled particle-fluid interactions in a confined domain. These findings provide critical insights for designing high-performance nanofluid-based cooling systems. Overall, the study confirms that nanofluids are a promising solution for enhanced thermal management in engineering applications.
References
[1] S. Kakaç, A. Pramuanjaroenkij, Heat Transfer Enhancement with Nanofluids, Springer, 2010.
[2] J. Buongiorno, “Convective transport in nanofluids,” J. Heat Transfer, vol. 128, pp. 240–250, 2006.
[3] M. Akbaki, M. Ghasemi, “Numerical investigation of nanofluid natural convection in cavities,” Int. J. Heat Mass Transfer, vol. 54, pp. 2710–2718, 2011.
[4] Y. Xuan, Q. Li, “Heat transfer enhancement of nanofluids,” Int. J. Heat Fluid Flow, vol. 21, pp. 58–64, 2000.
[5] S. M. S. Murshed, K. C. Leong, C. Yang, “Enhanced thermal conductivity of TiO₂-water nanofluids,” Int. J. Thermal Sci., vol. 44, pp. 367–373, 2005.
[6] W. Yu, H. Xie, “A review on nanofluids: preparation, stability mechanisms, and applications,” J. Nanomater., 2012.
[7] P. S. Ghosh, A. K. Das, “Numerical study of nanofluid convection in square cavity,” Appl. Math. Model., vol. 36, pp. 1681–1695, 2012.
[8] S. M. A. Bianco, L. M. Rossi, “Brownian motion effects in nanofluids,” Phys. Fluids, vol. 23, 2011.
[9] A. K. Singh, R. K. Mishra, “Numerical simulation of Al₂O₃–water nanofluid in a heated cavity,” Numer. Heat Transfer A, vol. 63, pp. 679–696, 2013.
[10] H. Mehrali, K. S. Toghraie, “Thermal conductivity of Al₂O₃ nanofluids: Experimental and numerical analysis,” Int. Commun. Heat Mass Transfer, vol. 39, pp. 1096–1101, 2012.
[11] M. Jang, S. Choi, “Role of Brownian motion in nanofluid heat transfer,” Appl. Phys. Lett., vol. 84, pp. 4316–4318, 2004.
[12] P. Eiamsa-ard, P. Promvonge, “Thermal performance of nanofluids in microchannels,” Int. J. Heat Mass Transfer, vol. 53, pp. 3345–3352, 2010.
[13] R. Prasher, P. Eapen, “Effect of particle clustering on nanofluid thermal conductivity,” Phys. Rev. Lett., vol. 94, 2005.
[14] A. Das, S. Putra, P. Thiesen, W. Roetzel, “Temperature dependence of thermal conductivity enhancement for nanofluids,” J. Heat Transfer, vol. 125, pp. 567–574, 2003.
[15] S. Patel, A. Kumar, “Simulation of nanofluid flow in heated cavities,” Comput. Fluids, vol. 101, pp. 103–114, 2014.
[16] X. Wang, A. Mujumdar, “Heat transfer characteristics of nanofluids: a review,” Int. J. Thermal Sci., vol. 46, pp. 1–19, 2007.
[17] M. Sheikholeslami, A. Ganji, “Numerical study of nanofluid natural convection in a square cavity,” Powder Technol., vol. 251, pp. 119–128, 2013.
[18] J. Li, W. Ding, “Investigation of Al₂O₃–water nanofluid in a vertical channel,” Int. J. Heat Mass Transfer, vol. 56, pp. 420–427, 2013.
[19] R. N. Patel, V. K. Sharma, “Influence of nanoparticle volume fraction on heat transfer,” Thermal Sci., vol. 19, pp. 1225–1236, 2015.
[20] S. K. Das, N. Putra, P. Thiesen, W. Roetzel, “Temperature dependence of thermal conductivity of nanofluids,” J. Heat Transfer, vol. 125, pp. 567–574, 2003.
[21] A. K. Singh, S. Kumar, “Nanofluid flow and heat transfer in porous cavities,” Powder Technol., vol. 253, pp. 90–101, 2014.
[22] Y. J. Ho, S. C. Lee, “Numerical investigation of nanofluid laminar flow in a microchannel,” Int. J. Heat Mass Transfer, vol. 55, pp. 6295–6306, 2012.
[23] L. C. Chow, “Nanofluid applications in electronics cooling,” Appl. Therm. Eng., vol. 26, pp. 770–779, 2006.
[24] T. S. Zhao, C. Y. Wang, “Nanofluid flow in porous media: a review,” Int. J. Heat Mass Transfer, vol. 48, pp. 3981–3991, 2005.
[25] S. Sundar, R. Sharma, “Heat transfer enhancement in nanofluids under natural convection,” Exp. Therm. Fluid Sci., vol. 36, pp. 1237–1246, 2012.
[26] P. E. Raithby, S. Choi, “Numerical simulation of nanofluid flows in rectangular cavities,” Int. J. Heat Fluid Flow, vol. 32, pp. 1171–1181, 2011.
[27] M. Sheikholeslami, R. Ellahi, “Magnetic field effects on nanofluid convection,” J. Mol. Liq., vol. 209, pp. 198–208, 2015.
[28] H. M. Paykani, A. A. Mohamad, “CFD analysis of nanofluid laminar convection in cavities,” Comput. Fluids, vol. 141, pp. 18–30, 2016.
[29] S. K. Das, S. Choi, W. Yu, “Nanofluids: Science and Technology,” Wiley-Interscience, 2007.
[30] A. K. Singh, R. Kumar, “Simulation of nanoparticle enhanced heat transfer in enclosures,” Appl. Therm. Eng., vol. 109, pp. 1052–1062, 2016.
You can download the Project files here: Download files now. (You must be logged in).
Do you need help with Multi-Scale Numerical Investigation of Buoyancy-Driven Nanofluid Heat Transfer with Particle-Scale Transport Effects in MATLAB? Don’t hesitate to contact our Tutors to receive professional and reliable guidance.








Responses