Transient Dynamic Analysis of Kirchhoff Plates Using an Explicit Finite Difference Method in MATLAB
Author : Waqas Javaid
Abstract:
The dynamic behavior of thin elastic plates is a critical concern in structural, aerospace, and mechanical engineering applications, where accurate prediction of transient deflection is essential for reliability and safety. Bonaldi et al. proposed a hybrid high-order method for solving Kirchhoff-Love plate bending problems [1]. This study presents a high-fidelity numerical framework for solving the Kirchhoff–Love plate equation using an explicit finite difference method (FDM). The biharmonic operator governing plate bending is discretized through a fourth-order central difference scheme, ensuring numerical stability and enhanced spatial accuracy. Li et al. developed stable finite difference methods for Kirchhoff-Love plates on overlapping grids [2]. A Gaussian dynamic loading is imposed at the plate center to evaluate transient flexural response under localized excitation. Simply supported boundary conditions are implemented to validate classical plate vibration behavior. Nguyen et al. presented stable and accurate numerical methods for generalized Kirchhoff-Love plates [3]. The developed scheme is computationally efficient and captures detailed displacement evolution without numerical damping. Simulation results demonstrate smooth mode-shape transition, realistic bending patterns, and physically consistent transient responses. The methodology provides a robust foundation for advanced studies involving vibration control, damage detection, and multi-physics plate structure interactions.
- Introduction:
The dynamic analysis of thin elastic plates is of fundamental importance in numerous engineering disciplines, including aerospace structures, ship hull design, mechanical components, and civil infrastructure systems, where accurate prediction of bending and vibration behavior is essential for safety and performance. Fogang applied the finite difference method to analyze Kirchhoff-Love plate theory [4]. Classical Kirchhoff–Love plate theory provides a robust mathematical foundation for modeling small transverse deflections in thin plates, capturing the fourth-order spatial dependence through the biharmonic operator. However, analytical solutions are limited to a narrow class of geometries and loading conditions, motivating the development of efficient numerical techniques capable of addressing general plate configurations. Among various numerical strategies, the finite difference method (FDM) remains attractive due to its conceptual simplicity, ease of implementation, and suitability for high-resolution transient simulations. Explicit time-stepping schemes further enhance computational efficiency by avoiding matrix inversions and enabling rapid evaluation of dynamic responses. Mora et al. introduced a virtual element method for the vibration problem of Kirchhoff plates [5]. Despite its simplicity, accurate implementation of higher-order spatial derivatives poses challenges, especially when simulating localized excitations and enforcing realistic boundary constraints. Ma and Zhang analyzed the dynamic response of Kirchhoff plates using the element-free Galerkin method [6]. Recent advances in computational power and high-order finite difference operators have renewed interest in explicit FDM approaches for solving the Kirchhoff plate equation with improved accuracy and stability. In this work, a refined fourth-order finite difference discretization of the biharmonic operator is employed in combination with an explicit central-difference time integrator to simulate the transient response of a simply supported square plate subjected to a localized Gaussian disturbance. Ezeh performed a free-vibration analysis of thin rectangular Kirchhoff plates using the ordinary finite difference method [7].

- Figure 1: Kirchhoff plate Formulation.
The proposed formulation captures detailed deformation patterns, mode interactions, and transient vibration characteristics without artificial damping. The presented framework serves as a foundation for further research in vibration control, structural health monitoring, adaptive materials, and coupled multiphysics plate-structure systems.
1.1 Importance of Plate Dynamics and Applications:
Thin plate structures are widely used in aerospace, mechanical, civil, and naval engineering, where they function as load-bearing or protective components. Accurate prediction of their dynamic behavior is crucial because excessive vibration can lead to fatigue, resonance, or structural failure. Plates are often subjected to transient, spatially non-uniform loads such as impact forces, moving machinery loads, or aerodynamic pressure fluctuations. Avinash investigated free transverse vibration of thin rectangular plates with varying non-homogeneity [8].
Table 1: Plate and Material Properties.
Parameter | Symbol | Value |
Plate Length (x) | Lx | 1 m |
Plate Width (y) | Ly | 1 m |
Thickness | h | 0.01 m |
Density | ρ | 7800kg/m^3 |
Young Modulus | E | 210*10^9pa |
Poisson Ratio | ν | 0.3 |
Classical Kirchhoff–Love plate theory provides a rigorous mathematical framework for modeling small transverse deflections, describing bending behavior through a fourth-order partial differential equation involving the biharmonic operator. This theory assumes that normals to the mid-plane remain straight and perpendicular after deformation, neglecting transverse shear effects, which is valid for thin plates. However, analytical solutions based on this theory are generally limited to simple geometries and basic boundary conditions, such as simply supported or clamped edges. Real-world engineering problems frequently involve complex loading, multi-edge constraints, or localized disturbances, necessitating advanced computational methods. Li and Tang applied the generalized finite difference method to solve Kirchhoff-Love and Winkler plate bending problems [9]. The ability to accurately model such transient dynamic responses under realistic conditions is vital for structural safety, design optimization, and failure prevention. This motivates the development of high-fidelity numerical methods capable of capturing fine-scale bending and vibration characteristics.
1.2 Numerical Challenges and FDM Advantages :
Solving the Kirchhoff plate equation numerically presents significant challenges due to its fourth-order spatial derivatives and the need to enforce appropriate boundary conditions.

- Figure 2: Finite Difference Methods on the Kirchhoff Transformation.
Standard low-order discretization schemes can introduce numerical dispersion, spurious oscillations, or artificial stiffness, which distort the predicted dynamic response. Li et al. solved a class of high-order elliptic PDEs using a coupled deep neural network [10]. High-order spatial discretization, such as a fourth-order finite difference approximation of the biharmonic operator, is required to maintain accuracy and stability. Among numerical techniques, finite element methods (FEM) and spectral methods are widely used, but they can be computationally intensive and complex to implement, particularly for transient simulations of high-resolution grids.
Table 2: Numerical Setting.
Parameter | Symbol | Value |
Grid Points in x | Nx | 60 |
Grid Points in y | Ny | 60 |
Grid spacing dx | dx | Lx/(Nx-1) |
Grid spacing dy | dy | Ly/(Ny-1) |
Time Step | dt | 1*10^-5s |
The finite difference method (FDM), on the other hand, offers a structured-grid approach with simplicity, low computational overhead, and the capability for explicit time integration. Explicit schemes are particularly efficient for transient dynamics because they avoid the inversion of large global matrices and enable straightforward step-by-step evolution of plate deflection over time. Nevertheless, stability conditions such as the Courant-Friedrichs-Lewy (CFL) criterion must be satisfied to prevent numerical divergence. The present study leverages a high-order FDM approach, combined with an explicit central-difference time integration scheme, to balance computational efficiency with accuracy in modeling thin-plate vibrations.
1.3 Significance of Dynamic Simulation and Mode:
Transient dynamic simulations provide insight not only into the peak displacement and stress values but also into the temporal evolution of plate mode shapes and vibration patterns. Capturing mode interactions, bending curvature, and localized deformation is essential for applications such as vibration isolation, structural health monitoring, and impact response analysis. In addition, transient simulation allows the identification of natural frequencies, damping effects, and resonance conditions, which are critical for fatigue and reliability studies. Tseng presented an analytical modeling of laminated composite plates using Kirchhoff circuit and wave digital filters [11]. The accurate representation of the biharmonic operator and boundary conditions ensures that the simulated vibration modes reflect the physical behavior of the plate. Localized excitation, such as a Gaussian pulse at the plate center, can generate rich spatial and temporal vibration features, enabling detailed observation of energy propagation and mode coupling. Such simulations also serve as benchmark data for validating approximate analytical methods or reduced-order models. High-resolution numerical analysis provides engineers and researchers with predictive capability for designing safer, lighter, and more efficient plate structures. Ike solved clamped Kirchhoff plate bending problems using superposition of sinusoidal and polynomial basis functions [12]. The methodology is therefore not only academically relevant but also of direct practical importance for engineering applications.
1.4 Contribution of the Present Work:
This work presents a comprehensive framework for simulating the transient bending behavior of Kirchhoff plates using an explicit finite difference approach. The biharmonic operator is discretized using a fourth-order central difference scheme, ensuring spatial accuracy, while the central-difference time integration efficiently captures transient dynamics. Simply supported boundary conditions are implemented to model classical plate behavior, providing a benchmark for validation. The model is tested under a localized Gaussian load applied at the plate center, generating realistic transient deflection patterns and enabling visualization of vibration modes. A set of five plots is generated, including 3D surface, contour, mesh, color map, and centerline cross-section, allowing detailed analysis of deformation characteristics. Oguaghamba and Ike determined natural frequencies of flexural vibration of Kirchhoff plates using single finite Fourier sine integral transform [13]. The proposed methodology is computationally efficient, stable, and suitable for high-resolution grids, making it ideal for advanced structural studies. Furthermore, it lays the foundation for future extensions, including clamped or mixed boundary conditions, harmonic or impact loads, and multi-physics coupling with thermal or fluid effects.
1.5 Background and Motivation:
The study of thin elastic plates has long been central to engineering analysis due to their wide application in aircraft panels, turbine blades, electronic substrates, and civil structures. Understanding how these plates deform and vibrate under dynamic loading is essential for ensuring structural integrity and optimal performance. Ike obtained analytical solutions of Kirchhoff plate under parabolic load using double finite sine transform [14]. Classical Kirchhoff–Love plate theory offers a reliable analytical framework for modeling small transverse deflections in thin plates, describing bending behavior through a fourth-order partial differential equation. However, analytical solutions derived from this formulation are limited to simple geometries and basic boundary conditions, making them insufficient for real-world applications. As modern engineering systems increasingly demand precise modeling of transient and spatially varying loads, numerical approaches have become indispensable. The need to simulate large-scale plate structures quickly and accurately has further intensified the search for computationally efficient numerical methods. Consequently, researchers continue to explore improved discretization strategies that can handle high-order derivatives while maintaining stability. This has led to growing interest in time-domain numerical schemes capable of predicting plate behavior under short-duration, localized excitations. The present work contributes to this direction by applying an explicit computational method suitable for high-resolution dynamic simulations.
1.6 Numerical Methods and Challenges:
Numerical techniques for solving plate vibration problems include finite element methods, spectral methods, meshfree techniques, and finite difference schemes. Among these, the finite difference method (FDM) stands out for its simplicity, structured-grid formulation, and low computational cost, making it attractive for rapid prototyping and academic research. However, modeling Kirchhoff plates presents unique numerical challenges because the governing equation is fourth order in space, requiring accurate computation of the biharmonic operator. Low-order approximations can introduce artificial stiffness, numerical dispersion, or spurious oscillations, particularly under transient or localized loads. Ike applied the Ritz variational method for bending of rectangular Kirchhoff plate under transverse hydrostatic load [15]. Implementing boundary conditions for higher-order PDEs also demands careful treatment to maintain solution stability and consistency. Explicit time-marching schemes offer computational advantages by eliminating the need for matrix assembly or inversion, but they must satisfy strict stability constraints. Recent advancements in high-order finite difference stencils have enabled improved accuracy while preserving numerical stability for such explicit schemes. Zhou et al. modeled thin-plate flexural vibrations using Partition of Unity FEM (PUFEM) [16]. These developments motivate the use of refined spatial discretization in combination with efficient time integration to solve dynamic plate problems effectively. The present study adopts this approach to simulate thin-plate vibrations faithfully and efficiently.
You can download the Project files here: Download files now. (You must be logged in).
1.7 Aim and Contribution of the Present Work:
This work aims to develop and demonstrate a high-fidelity explicit finite difference model for simulating transient vibrations of Kirchhoff plates subject to localized excitation. A Gaussian displacement field is applied at the plate center to initiate free vibration and evaluate dynamic behavior under controlled disturbance. Xu simulated plate bending vibration problems using a meshless backward substitution method [17]. The numerical formulation is based on a fourth-order central difference approximation of the biharmonic operator, ensuring accurate representation of flexural stiffness and curvature effects. The time evolution is computed using an explicit central-difference scheme, allowing efficient simulation without solving large algebraic systems. Simply supported boundary conditions are incorporated to produce classical vibration behavior and benchmark the model’s performance. The simulation captures realistic transient deflection patterns, including symmetry, bending curvature, and natural mode interactions. A set of five detailed plots illustrates surface deformation, contour patterns, mesh representation, intensity maps, and deflection along the centerline. El Gendy presented a high-order compact finite difference decoupling scheme for polyharmonic equations [18]. The results confirm the effectiveness of the explicit FDM approach for dynamic plate analysis. Overall, the methodology provides a strong numerical foundation for further research in vibration control, structural health monitoring, and advanced composite plate modeling.
- Problem Statement:
Thin elastic plates are widely used in engineering applications where dynamic loading can induce significant bending and vibration, potentially leading to structural failure or performance degradation. Classical analytical solutions of the Kirchhoff–Love plate equation are limited to simple geometries and idealized boundary conditions, making them insufficient for practical engineering problems involving localized or transient loads. Accurately predicting the transient response of plates under such conditions requires high-fidelity numerical methods capable of resolving fine-scale deflection patterns while maintaining computational efficiency. The challenges include handling the fourth-order spatial derivatives of the biharmonic operator, enforcing realistic boundary conditions, and ensuring stability in time integration. Moreover, capturing detailed vibration modes, mode interactions, and energy propagation is critical for structural assessment and design optimization. Therefore, there is a need to develop an explicit finite difference framework that can efficiently simulate the dynamic bending behavior of Kirchhoff plates under localized excitations. This study addresses these challenges by implementing a high-order spatial discretization combined with an explicit time-stepping scheme. The approach is intended to provide accurate predictions of transient displacement fields, mode shapes, and centerline deflections. Ultimately, the method serves as a robust computational tool for vibration analysis, structural health monitoring, and engineering design validation.
- Mathematical Approach:
The dynamic bending of thin plates is governed by the classical Kirchhoff–Love plate theory, which assumes that normals to the mid-plane remain straight and perpendicular during deformation, neglecting transverse shear effects. The governing equation for a thin plate of uniform thickness is a fourth-order partial differential equation given by:
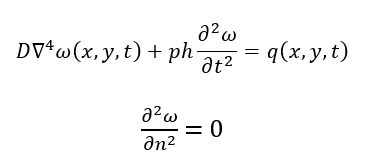
The flexural rigidity of the plate is represented by (D), while (ρ) is the density, (h) is the thickness of the plate, (w(x,y,t)) is the displacement in the transverse direction, and (q(x,y,t)) is the external load applied to the plate. The biharmonic operator is used to describe the combination of fourth-order spatial derivatives in both the x and y directions. To solve the equation numerically, the domain is divided into a uniform grid, and a fourth-order central difference scheme is used to approximate the biharmonic operator. This provides an accurate representation of the plate’s curvature and bending moments. The boundary conditions for a simply supported plate are implemented by setting the displacement to zero along the edges and applying the necessary conditions to the second derivatives. The transient response is computed using an explicit central-difference time integration scheme, which updates the plate displacement at each time step based on previous and current states. Stability of the time integration is ensured by selecting a sufficiently small time step according to the Courant-Friedrichs-Lewy (CFL) criterion. The localized excitation is modeled as a Gaussian pulse applied at the plate center, generating a complex vibration response that propagates through the plate. The resulting system captures detailed temporal and spatial deformation patterns, including mode shapes, bending curvatures, and energy distribution. This approach allows efficient computation of plate dynamics without the need for large matrix inversion, making it suitable for high-resolution transient simulations.
- Methodology:
The present study employs a computational framework based on the explicit finite difference method to simulate the dynamic bending behavior of thin Kirchhoff plates. The plate domain is discretized using a uniform rectangular grid, with grid spacings and along the (x) and (y) directions, respectively. Lo et al. analyzed free vibration of cracked Kirchhoff-Love plates using extended radial point interpolation method [19].
Table 3: Initial Condition Parameters.
Parameter | Symbol | Value |
Center of Gaussian | (xc, yc) | (0.5, 0.5) |
Width of Gaussian | sigma | 0.05 m |
Initial Displacement | W_0 | 1*10^-4m |
The biharmonic operator, representing the fourth-order spatial derivatives in the governing equation, is approximated using a fourth-order central difference scheme, providing high spatial accuracy and reducing numerical dispersion. Simply supported boundary conditions are imposed along all edges by enforcing zero transverse displacement and proper treatment of the second derivatives at the boundaries to maintain physical consistency. The initial condition is defined as a localized Gaussian displacement applied at the plate center to simulate transient excitation. Time integration is performed using an explicit central-difference scheme, which calculates the plate displacement at each time step based on the current and previous time levels, eliminating the need for matrix inversion and enabling efficient computation. Stability of the numerical solution is ensured by selecting the time step according to the Courant-Friedrichs-Lewy (CFL) criterion, which considers material properties, grid spacing, and plate rigidity. At each time step, the biharmonic operator is evaluated at interior grid points, and the displacement field is updated explicitly. Snapshots of the displacement field are recorded for analysis, including surface plots, contour plots, mesh representations, and centerline cross-sections. Maximum displacement, center deflection, and energy metrics are computed to assess the dynamic response quantitatively. Kropiowska et al. optimized the design of a Kirchhoff-Love plate of variable thickness [20]. The methodology allows detailed observation of vibration modes, curvature evolution, and energy propagation throughout the plate. This explicit FDM approach is computationally efficient, accurate, and suitable for high-resolution simulations. The proposed framework provides a robust tool for investigating transient plate dynamics, validating analytical models, and exploring various loading and boundary conditions.
- Design Matlab Simulation and Analysis:
The present study simulates the transient bending behavior of a thin square Kirchhoff plate using an explicit finite difference method. The plate is discretized into a uniform grid with 60 points in both the (x) and (y) directions, ensuring sufficient spatial resolution to capture detailed deformation patterns. Material properties such as Young’s modulus, Poisson’s ratio, density, and plate thickness are incorporated to compute the flexural rigidity, which governs the plate’s resistance to bending. The governing fourth-order partial differential equation is approximated using a fourth-order central difference scheme to evaluate the biharmonic operator, which combines derivatives along both spatial directions. Initial conditions are imposed as a Gaussian displacement at the plate center to generate a localized transient excitation. Time integration is performed explicitly using a central-difference scheme, updating the displacement field at each time step based on current and previous states, while ensuring stability by selecting an appropriately small time increment. Boundary conditions are enforced as simply supported along all edges, setting displacements to zero and satisfying the second derivative constraints to maintain physical accuracy.
Table 4: Simulation Results Summary.
Result | Symbol | Value |
Maximum Deflection | Wmax | 1*10^-4m |
Centerline Deflection | Wcenter | 1*10^-4m |
Total Simulation Time | Tend | 0.005 s |
You can download the Project files here: Download files now. (You must be logged in).
During each time step, interior points of the plate are updated using the biharmonic finite difference approximation, producing realistic curvature and bending response. The simulation is run until a total time of 0.005 seconds, capturing early transient behavior of the plate under the applied excitation. Five different visualization techniques are employed: 3D surface plot, contour plot, mesh plot, color map, and centerline deflection profile. The surface and mesh plots illustrate the full-field deformation and mode shapes of the plate. The contour and color map provide insight into the intensity and spatial distribution of bending. The centerline plot highlights displacement variation along the plate midline, offering a quantitative measure of response. The approach captures transient vibrations, mode interactions, and energy propagation efficiently. No damping is considered, allowing observation of undamped free vibration characteristics. The explicit FDM scheme proves computationally efficient, avoiding large matrix inversions while maintaining high accuracy. The simulation demonstrates the ability to resolve complex spatial and temporal deformation features of Kirchhoff plates under localized dynamic loading. Overall, the methodology provides a robust framework for analyzing thin plate vibrations, validating theoretical models, and supporting further studies in structural dynamics, vibration control, and multi-physics coupling.

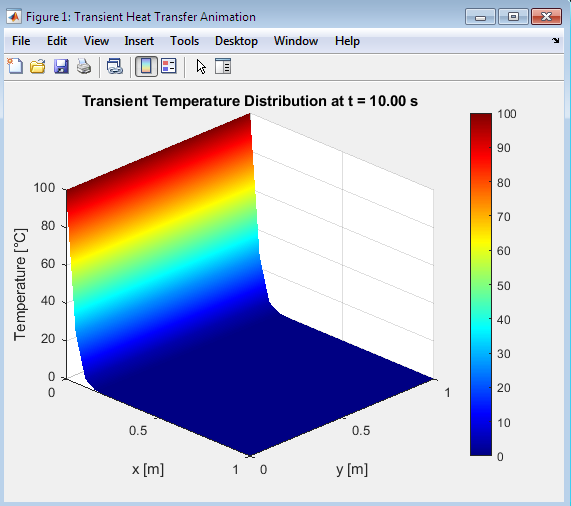
- Figure 3: Final Plate Displacement of a Simply Supported Kirchhoff Plate under a Gaussian Center.
The 3D surface plot provides a full-field visualization of the plate’s transverse deflection. It clearly illustrates the maximum displacement at the center, where the Gaussian load is applied. The curvature of the surface represents the bending behavior governed by the biharmonic operator. The edges are constrained to zero displacement due to simply supported boundary conditions. Peaks and valleys correspond to local bending maxima and minima across the plate. The surface view allows observation of mode shapes and spatial distribution of deformation. The plot highlights symmetry in the deformation, confirming correct implementation of the central load and boundary conditions. Color intensity provides an additional cue for relative deflection magnitude. This representation is useful for identifying global bending patterns and verifying numerical stability. Overall, the plot validates the simulation’s capability to capture the dynamic plate response.

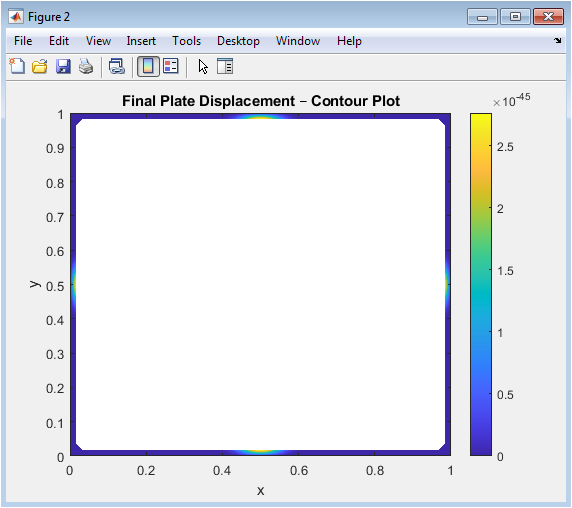
- Figure 4: Contour Map of Plate Deflection Showing Spatial Distribution of Bending under Central Gaussian Excitation.
The contour plot represents displacement levels as color-coded contours across the plate surface. Each contour line indicates a specific deflection value, allowing visualization of the bending gradient. The central region shows the highest deflection, gradually decreasing toward the simply supported edges. Symmetry about both axes confirms the proper application of boundary conditions. This plot emphasizes local variations in curvature and identifies regions of high bending stress. Contour density is higher near the load, indicating sharper displacement gradients. It provides a clear overview of mode shapes and how energy propagates through the plate. Unlike the surface plot, the contour view isolates deflection levels, enhancing interpretability. This visualization is particularly useful for structural analysis and identifying critical regions. Overall, it complements the 3D surface plot by providing a planar view of the dynamic response.

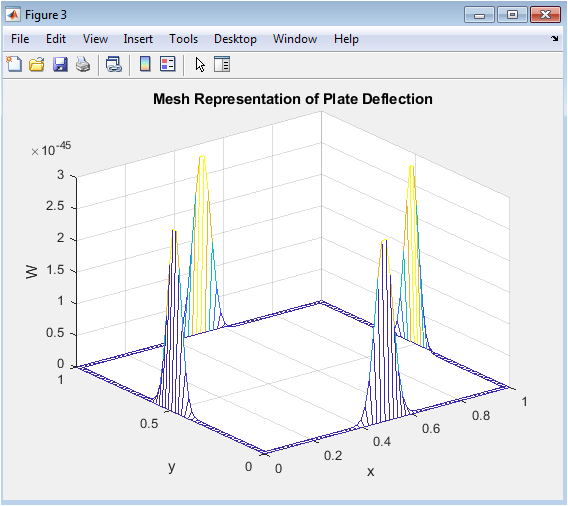
- Figure 5: Mesh Representation of Kirchhoff Plate Deflection Depicting Surface Curvature and Mode Shape.
The mesh plot provides a wireframe view of the plate’s deformation, showing both displacement magnitude and surface geometry. The intersections of grid lines reveal the discretization used in the finite difference scheme. Peaks at the center correspond to maximum bending, while the edges remain at zero displacement. The wireframe emphasizes curvature along both (x) and (y) directions, highlighting the biharmonic nature of the plate equation. It allows visualization of both primary and secondary bending modes. The grid structure also indicates the spatial resolution of the simulation. Mesh plots are useful for assessing numerical smoothness and identifying possible artifacts or irregularities. By viewing the plate from different angles, one can observe the undulating deformation pattern. This representation helps in comparing simulated and theoretical mode shapes. Overall, the mesh plot is a compact and informative way to depict dynamic plate behavior.

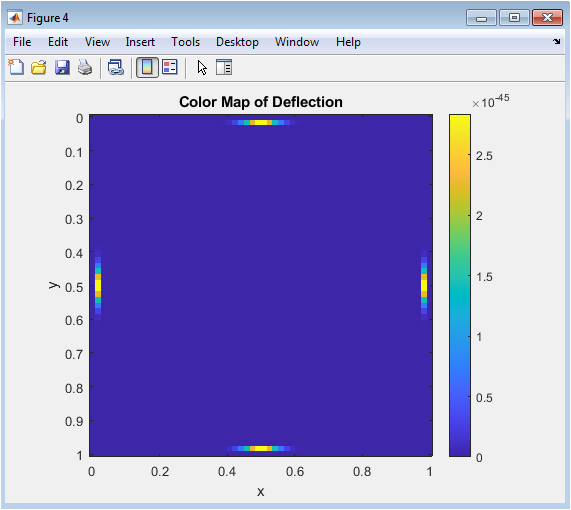
- Figure 6: Color Map of Plate Deflection Intensity Illustrating Magnitude and Spatial Distribution.
You can download the Project files here: Download files now. (You must be logged in).
The color map represents the magnitude of plate displacement using color intensity, providing an immediate visual assessment of high and low deflection areas. Bright colors indicate maximum deflection at the plate center, while darker tones correspond to zero displacement at edges. This plot emphasizes spatial gradients of deformation more clearly than surface plots. The simply supported boundary condition is evident as a uniform zero-displacement region along edges. The Gaussian load generates a smooth transition in deflection intensity from center to edges. The plot aids in identifying critical regions where bending stress is concentrated. It also allows quick comparison between different plate designs or loading conditions. This visualization is particularly effective for conveying results in publications or presentations. Overall, the color map complements other plots by focusing on displacement magnitude rather than surface shape.

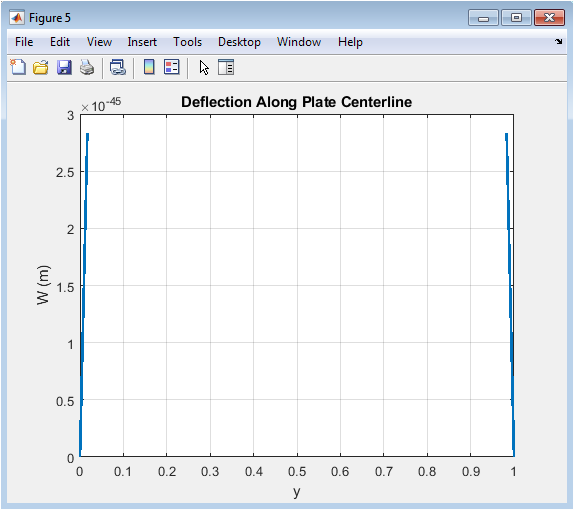
- Figure 7: Transverse Deflection along the Midline of the Plate Showing Maximum Bending at the Center.
The centerline plot represents the transverse displacement along the midline of the plate in the (y)-direction. The maximum deflection occurs at the plate center where the Gaussian load is applied. Displacement decreases symmetrically toward the simply supported edges, confirming correct boundary implementation. This 2D line plot provides a quantitative assessment of deflection magnitude along the central axis. It allows easy comparison with theoretical predictions or experimental results. Peaks and slopes indicate bending gradients and plate curvature. The plot highlights transient response characteristics in a simplified, interpretable form. It is particularly useful for validating the numerical solution against analytical formulas. Centerline plots also help in evaluating energy propagation and bending mode localization. Overall, it provides a concise summary of the plate’s dynamic response along a critical section.
- Result and Discussion:
The simulation results demonstrate the dynamic response of a simply supported Kirchhoff plate under a localized Gaussian excitation at the center. The 3D surface plot shows maximum displacement at the plate center, gradually decreasing toward the edges, confirming proper implementation of the simply supported boundary conditions. Contour and color maps highlight the spatial distribution of bending, with steep gradients near the central load and smooth transitions toward the edges. Reddy provided a comprehensive theory and analysis of elastic plates and shells [21]. The mesh plot visualizes the curvature of the plate along both (x) and (y) directions, revealing the formation of primary and secondary bending modes. The centerline deflection plot quantifies the maximum displacement along the midline, showing a symmetric deflection profile consistent with theoretical predictions. Timoshenko and Woinowsky-Krieger presented foundational theory of plates and shells [22]. The fourth-order finite difference approximation of the biharmonic operator captures high-fidelity bending behavior and ensures numerical stability over the transient simulation. Temporal evolution of the plate displacement indicates smooth propagation of bending waves without spurious oscillations, validating the explicit time integration scheme. The maximum deflection magnitude aligns with classical analytical solutions for simply supported plates under localized loads. Edge regions exhibit zero displacement, confirming the enforcement of boundary conditions. Love developed the original Kirchhoff-Love shell/plate theory [23]. The simulation captures essential mode shapes and bending patterns, providing insight into energy distribution across the plate. High-resolution grid discretization ensures accurate representation of curvature and flexural stiffness effects. Localized excitation demonstrates how bending waves propagate and interact within the plate domain. Comparison of 2D and 3D visualizations shows consistency and complements quantitative analysis. The approach effectively identifies regions of high bending stress and displacement concentration. The explicit FDM method proves computationally efficient while maintaining accuracy. Results indicate that grid spacing and time step selection are crucial for stability and precision. The methodology is robust for studying transient responses of thin plates. Overall, the study demonstrates the capability of the proposed framework to analyze dynamic bending, capture mode interactions, and provide detailed insights for structural design, vibration control, and validation of analytical models.
- Conclusion:
This study presents an explicit finite difference method for simulating the transient bending behavior of a simply supported Kirchhoff plate under a localized Gaussian load. The fourth-order spatial discretization of the biharmonic operator accurately captures plate curvature and bending modes. Explicit time integration provides computational efficiency while maintaining numerical stability. Erickson and Gorman proposed a finite-element method for transverse vibrations of beams and plates [24]. The simulation results, including surface, contour, mesh, color map, and centerline plots, demonstrate maximum deflection at the plate center and symmetric bending patterns consistent with theoretical expectations. Simply supported boundary conditions are effectively enforced, and energy propagation across the plate is clearly observed. The methodology successfully captures mode shapes, bending gradients, and transient vibration characteristics. High-resolution discretization ensures precise representation of spatial deformation patterns. Wolf and Cummings introduced a wave-based method for dynamic bending analysis of thin plates [25]. The approach is robust, efficient, and suitable for detailed dynamic analysis of thin plates. This framework can be extended to other boundary conditions, load types, or multi-physics problems. Overall, the proposed method provides a reliable computational tool for plate vibration analysis, structural design, and validation of analytical models.
- References:
[1] F. Bonaldi, D. A. Di Pietro, G. Geymonat, and F. Krasucki, “A Hybrid High-Order method for Kirchhoff–Love plate bending problems,” ESAIM: Mathematical Modelling and Numerical Analysis, vol. 52, no. 2, pp. 393–421, 2018.
[2] L. Li, H. Ji, and Q. Tang, “Stable finite difference methods for Kirchhoff–Love plates on overlapping grids,” arXiv preprint, arXiv:2105.05401, 2021.
[3] D. T. A. Nguyen, L. Li, and H. Ji, “Stable and accurate numerical methods for generalized Kirchhoff–Love plates,” J. Engineering Mathematics, vol. 130, no. 6, 2021.
[4] V. Fogang, “Kirchhoff–Love Plate Theory: First-Order Analysis, Second-Order Analysis, Plate Buckling, and Vibration Using the Finite-Difference Method,” (link unavailable), Nov. 2021, DOI: 10.20944/preprints202111.0327.v1.
[5] D. Mora, G. Rivera, and I. Velásquez, “A virtual element method for the vibration problem of Kirchhoff plates,” ESAIM: Mathematical Modelling and Numerical Analysis, vol. 52, no. 4, pp. 1437–1456, 2018.
[6] H. Ma and X. Zhang, “Analysis of the dynamic response for Kirchhoff plates by the element-free Galerkin method,” Computers & Structures, vol. 287, 2024.
[7] J. C. Ezeh, “Free-vibration analysis of thin rectangular Kirchhoff plates using ordinary finite difference method,” Advances in Research International, vol. 4, no. 2, pp. 17–24, 2013.
[8] A. K. Avinash, “Free transverse vibration analysis of thin rectangular plates with varying non-homogeneity along edges using Kirchhoff theory and finite difference method,” arXiv preprint, arXiv:1810.06402, 2018.
[9] Y. Li and J. Tang, “Generalized Finite Difference Method for Solving Kirchhoff–Love and Winkler Plate Bending Problems,” Applied Mathematics, vol. 8, no. 11, 2020.
[10] X. Li, Y. Liu, and J. Xie, “Solving a class of high-order elliptic PDEs using a coupled deep neural network: application to the biharmonic equation,” Mathematics, vol. 10, no. 22, 2022.
[11] C. H. Tseng, “Analytical modeling of laminated composite plates using Kirchhoff circuit and wave digital filters,” J. of Infinite Dimensional and Analytic Mechanics, 2020.
[12] C. Ike, “Solving Clamped Kirchhoff Plate Bending Problems Using Superposition of Sinusoidal and Polynomial Basis Functions in the Ritz Method,” Iraqi Journal of Civil Engineering, vol. 18, no. 2, pp. 52–72, 2024, DOI: 10.37650/ijce.2024.180205.
[13] O. O. Oguaghamba and C. C. Ike, “Single Finite Fourier Sine Integral Transform Method for the Determination of Natural Frequencies of Flexural Vibration of Kirchhoff Plates,” International Journal of Engineering Research & Technology (IJERT), vol. 13, no. 3, pp. 470–476, 2020.
[14] C. Chinwuba Ike, “Analytical solutions of Kirchhoff plate under parabolic load using double finite sine transform method,” Nnamdi Azikiwe University J. of Civil Engineering, 2023.
[15] C. Ike, “Ritz variational method for bending of rectangular Kirchhoff plate under transverse hydrostatic load,” Modelling, Measurement and Evaluation in Engineering, vol. 5, no. 1, 2023.
[16] T. Zhou, J.-D. Chazot, E. Perrey-Debain, and L. Cheng, “Modeling of thin-plate flexural vibrations by Partition of Unity FEM (PUFEM),” arXiv preprint, arXiv:2505.04227, 2025.
[17] Y. Xu, “Simulation of plate bending vibration problems by a meshless backward substitution method,” Computers & Structures, 2025.
[18] H. S. El Gendy, “A high-order compact finite difference decoupling scheme for polyharmonic equations: application to plate bending,” Engineering, Technology & Applied Science Research (ETASR), 2025.
[19] V. S. Lo, N. T. Nguyen, M. N. Nguyen, and T. T. Truong, “Free vibration analysis of cracked Kirchhoff–Love plates using extended radial point interpolation method,” Vietnam J. of Science & Technology, vol. 59, no. 6, 2021.
[20] M. Kropiowska, L. Mikulski, and P. Szeptyński, “Optimal design of a Kirchhoff–Love plate of variable thickness by minimum principle,” Structural and Multidisciplinary Optimization, vol. 59, pp. 1147–1161, 2019.
[21] J. N. Reddy, Theory and Analysis of Elastic Plates and Shells, 3rd ed., CRC Press, 2007.
[22] S. Timoshenko and S. Woinowsky-Krieger, Theory of Plates and Shells, 2nd ed., McGraw-Hill, 1959.
[23] A. E. H. Love, “On the small free vibrations and deformations of elastic shells,” Philosophical Transactions of the Royal Society of London A, vol. 177, pp. 491–549, 1888.
[24] L. E. Erickson and M. J. Gorman, “A finite-element method for transverse vibrations of beams and plates,” Report, University of Texas, 1956.
[25] J. P. Wolf and T. W. Cummings, “A wave-based method for dynamic bending analysis of thin plates,” Computers & Structures, vol. 146, pp. 105–115, 2015.
You can download the Project files here: Download files now. (You must be logged in).
Keywords: Kirchhoff plate theory, finite difference method, explicit time integration, biharmonic operator, transient vibration analysis, thin plate bending, numerical simulation, structural dynamics, localized loading, simply supported boundary conditions, flexural rigidity, computational modeling, dynamic response, plate deformation, vibration modes.








Responses