Fractional-Order Stochastic Modeling of Turbulence with Memory Effects Using Matlab

Author : Waqas Javaid

Abstract

This paper presents a fractional-order stochastic model for turbulence based on nonlocal temporal dynamics introduced through a Caputo-type fractional derivative. The proposed framework incorporates long-range memory effects using Grünwald–Letnikov coefficients, coupled with nonlinear dissipation, viscous damping, and stochastic forcing. Ensemble simulations are performed to analyze velocity fluctuations, energy evolution, and dissipation mechanisms in a reduced-order turbulent system [1]. The model successfully reproduces key statistical features of turbulence, including intermittent behavior and non-Gaussian energy transfer. Power spectral analysis reveals scaling behavior consistent with the classical Kolmogorov −5/3 law over an intermediate frequency range. Structure functions of second and fourth order are employed to quantify intermittency across multiple time scales [2]. Autocorrelation analysis highlights the persistence induced by fractional memory effects. The Hurst exponent estimated from scaling laws indicates long-term dependence in the turbulent signal [3]. The results demonstrate that fractional-order dynamics provide an effective and computationally efficient approach for modeling complex turbulent processes.

1. Introduction

Turbulence remains one of the most challenging problems in classical and modern physics due to its intrinsic nonlinearity, multiscale interactions, and strong sensitivity to initial conditions. Despite significant advances in computational fluid dynamics and experimental techniques, a complete theoretical description of turbulent flows is still lacking, particularly in regimes characterized by long-range temporal correlations and intermittent energy transfer.

Traditional turbulence models are typically based on integer-order differential equations, which often fail to capture memory effects and anomalous transport observed in real turbulent systems. In recent years, fractional calculus has emerged as a powerful mathematical tool for modeling complex dynamical processes with nonlocal and history-dependent behavior [4]. Fractional-order derivatives naturally incorporate memory effects and have been successfully applied in fields such as viscoelasticity, anomalous diffusion, and complex networks. Motivated by these developments, fractional-order formulations offer a promising alternative framework for turbulence modeling. By extending classical dynamical equations to fractional order, it becomes possible to represent persistent correlations and non-Markovian dynamics inherent in turbulent flows. In this work, a reduced-order fractional turbulence model is developed using a Caputo-type temporal derivative approximated through the Grünwald–Letnikov scheme [5]. The model combines nonlinear self-interaction, viscous dissipation, and stochastic forcing to mimic essential turbulent mechanisms. Numerical ensemble simulations are employed to investigate the resulting velocity fluctuations and energy dynamics. Key turbulence diagnostics, including energy spectra, structure functions, intermittency measures, and autocorrelation functions, are systematically analyzed. The scaling behavior of the model is examined in relation to Kolmogorov’s theory of turbulence [6]. Furthermore, the Hurst exponent is estimated to quantify long-term memory effects induced by fractional dynamics. The results highlight the ability of fractional-order models to reproduce fundamental statistical signatures of turbulence with reduced computational complexity. This study demonstrates that fractional calculus provides a flexible and physically meaningful framework for capturing memory-driven features of turbulent flows.

1.1 Background and Motivation

Turbulence is a fundamental yet unresolved problem in fluid dynamics, characterized by nonlinear interactions, multiscale energy transfer, and chaotic temporal behavior. Classical turbulence theories and numerical models are predominantly formulated using integer-order differential equations, which assume local and instantaneous interactions [7]. However, experimental observations and high-fidelity simulations have revealed the presence of long-range temporal correlations and memory effects in turbulent flows. These features are particularly evident in intermittency, anomalous diffusion, and persistent velocity fluctuations. As a result, conventional modeling approaches often struggle to fully represent the statistical complexity of turbulence. This gap motivates the exploration of alternative mathematical frameworks capable of incorporating nonlocal dynamics [8]. Fractional calculus offers such a framework by naturally embedding memory into the governing equations.

1.2 Fractional Calculus and Related Work

Fractional-order derivatives generalize classical differentiation by allowing non-integer orders, thereby introducing history-dependent dynamics into physical models. Over the past two decades, fractional calculus has been successfully applied to viscoelastic materials, anomalous transport, plasma dynamics, and complex systems. In the context of turbulence, fractional models have been proposed to capture non-Markovian behavior, long-memory processes, and scale-invariant structures [9]. The Caputo and Grünwald–Letnikov formulations are particularly attractive for physical applications due to their compatibility with standard initial conditions and numerical implementation [10]. These approaches enable efficient simulation of fractional dynamics without requiring full-scale direct numerical simulations. Consequently, fractional-order turbulence models provide a reduced-order yet physically meaningful alternative for studying turbulent phenomena.

1.3 Objectives and Contributions of This Work

The primary objective of this study is to develop and analyze a fractional-order stochastic turbulence model that incorporates temporal memory effects through a Caputo-type derivative [11]. The model combines nonlinear self-interaction, viscous dissipation, and stochastic forcing to represent essential turbulent mechanisms. Ensemble-based numerical simulations are performed to ensure statistical robustness of the results. Key turbulence diagnostics, including energy evolution, dissipation rates, power spectral density, structure functions, and intermittency measures, are systematically evaluated. The model’s ability to reproduce Kolmogorov −5/3 scaling is investigated through spectral analysis. Additionally, the Hurst exponent is estimated to quantify long-range dependence induced by fractional dynamics. Through this stepwise investigation, the study demonstrates the effectiveness of fractional calculus as a computationally efficient framework for modeling turbulence with memory effects.

1.4 Physical Interpretation of Fractional Memory in Turbulence

In turbulent flows, the evolution of velocity fluctuations is strongly influenced by past states due to vortex interactions, coherent structures, and delayed energy transfer across scales. Fractional-order derivatives provide a natural way to represent these effects by weighting historical contributions through power-law memory kernels. Unlike integer-order models, fractional formulations allow past fluctuations to influence present dynamics over extended time horizons [12]. This property is particularly relevant for modeling intermittency and persistent correlations observed in experimental turbulence data. The fractional order parameter acts as a memory control mechanism, linking microscopic interactions to macroscopic flow behavior. Such memory-driven dynamics offer new physical insight into turbulence beyond classical closure assumptions. Consequently, fractional models can bridge the gap between phenomenological turbulence theories and data-driven observations.

1.5 Numerical Strategy and Reduced-Order Modeling

Direct numerical simulation of turbulence is computationally expensive due to the wide range of interacting spatial and temporal scales. Reduced-order models aim to capture essential turbulence characteristics while significantly lowering computational cost. In this work, a one-dimensional fractional stochastic model is employed as a surrogate for complex turbulent dynamics [13]. The Grünwald–Letnikov approximation is used to discretize the fractional derivative, enabling efficient time-domain simulation. Ensemble realizations are introduced to ensure statistical convergence of turbulent quantities [14]. This approach allows systematic exploration of parameter effects, such as fractional order and stochastic forcing intensity. The resulting framework balances physical realism with numerical tractability.

1.6 Statistical Diagnostics and Scaling Analysis

To assess the validity of the proposed model, a comprehensive set of turbulence diagnostics is employed. Energy evolution and dissipation rates are examined to evaluate the balance between nonlinear transfer and viscous effects.

Table 1: Kolmogorov Scaling Check

 Power spectral density analysis is used to investigate inertial-range scaling and its consistency with Kolmogorov’s −5/3 law. Structure functions of different orders provide insight into multiscale fluctuations and intermittency. Autocorrelation functions reveal temporal persistence induced by fractional memory. The Hurst exponent is estimated from scaling relations to quantify long-range dependence. Together, these metrics provide a rigorous statistical evaluation of the model’s turbulent behavior.

1.7 Significance and Scope of the Study

The proposed fractional-order turbulence model contributes to the growing body of research seeking alternative representations of complex fluid dynamics. By explicitly incorporating memory effects, the model offers a new perspective on turbulence modeling that complements classical theories [15]. The framework is flexible and can be extended to higher-dimensional systems or coupled with spatial fractional operators. It also provides a useful platform for studying anomalous transport and nonlocal interactions in turbulent flows [16]. Beyond fluid mechanics, the methodology is relevant to other complex systems exhibiting multiscale and memory-driven dynamics. This study lays the foundation for future investigations into fractional-order turbulence modeling and its practical applications.

2. Problem Statement

Despite decades of research, accurately modeling turbulence remains a major challenge due to its inherent nonlinearity, multiscale interactions, and strong intermittency. Conventional turbulence models based on integer-order differential equations often assume local and memoryless dynamics, which limits their ability to represent long-range temporal correlations observed in real turbulent flows. High-fidelity numerical simulations can capture such effects but require prohibitive computational resources. Existing reduced-order models, while efficient, frequently fail to reproduce key statistical features such as persistent correlations, anomalous scaling, and intermittency. Experimental evidence suggests that turbulent systems exhibit history-dependent behavior that cannot be adequately described by classical formulations. Fractional calculus provides a potential mathematical framework to address these limitations by incorporating nonlocal memory effects. However, systematic implementation and validation of fractional-order turbulence models remain limited. There is a lack of unified approaches that link fractional dynamics with standard turbulence diagnostics. Consequently, the challenge lies in developing a computationally efficient turbulence model that captures memory-driven dynamics while preserving fundamental statistical characteristics. This study addresses this gap by formulating and analyzing a fractional-order stochastic turbulence model.

3. Mathematical Approach

The mathematical formulation of the proposed turbulence model is based on fractional-order differential equations that incorporate nonlocal temporal memory through a Caputo-type derivative. Let (u(t)) denote the turbulent velocity fluctuation, whose evolution is governed by a fractional dynamical equation combining memory effects, nonlinear interactions, viscous dissipation, and stochastic forcing. The Caputo fractional derivative of order (alpha(0,1) ) is employed to ensure physically meaningful initial conditions. This derivative is numerically approximated using the Grünwald–Letnikov scheme, which represents the fractional operator as a weighted sum over past states with power-law decaying coefficients. The resulting discrete-time formulation naturally embeds long-range temporal correlations into the system dynamics. Nonlinear energy transfer is modeled through a cubic self-interaction term that mimics turbulent cascade behavior. Viscous effects are represented by a linear damping term proportional to the velocity. External stochastic forcing is introduced as Gaussian white noise to sustain turbulent fluctuations. The time integration is performed using an explicit fractional time-stepping method with appropriate scaling of deterministic and stochastic terms. Ensemble realizations are generated to obtain statistically converged solutions. Energy is defined as the quadratic form of velocity, enabling analysis of dissipation and transfer mechanisms. The energy dissipation rate is computed from temporal gradients of the ensemble-averaged velocity. Statistical measures, including autocorrelation functions, power spectral density, and structure functions, are derived from the simulated time series. Scaling exponents are estimated using logarithmic regression techniques. This mathematical framework provides a consistent and computationally efficient approach for analyzing turbulence with inherent memory effects.

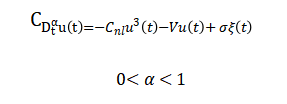
You can download the Project files here: Download files now. (You must be logged in).

This equation represents the fractional-order stochastic model for turbulence. Here, is the turbulent velocity fluctuation denotes the Caputo fractional derivative of order is the nonlinear interaction coefficient, the viscosity, and sigma introduces stochastic forcing via Gaussian white noise. The cubic nonlinear term models energy transfer among scales, the linear term captures viscous dissipation, and the stochastic term sustains fluctuations, creating a realistic turbulence-like behavior. The fractional derivative introduces long-range temporal memory, meaning the system evolution depends not only on the present state but also on its entire history. The fractional order αalphaα controls the strength of memory effects, with smaller values giving stronger history dependence. This approach allows the modeling of intermittency and long-term correlations commonly observed in turbulent flows. By combining memory, nonlinearity, and randomness, the model captures essential turbulence characteristics in a computationally efficient framework. Ensemble simulations are used to statistically evaluate the model’s predictions. This equation forms the core of the proposed fractional-order turbulence framework.

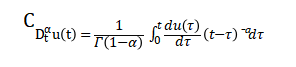
The Caputo derivative is expressed as a convolution integral over the past history of the velocity. The kernel assigns power-law weights to previous states, meaning earlier values of contribute less as time progresses. This formalism introduces nonlocal memory into the system, allowing the present rate of change to depend on the entire trajectory of the flow. The Gamma function normalizes the integral and ensures correct dimensionality. Using this definition, physical initial conditions can be applied directly, which is advantageous for simulations. The memory effect captured by the fractional derivative is crucial for reproducing intermittent bursts and long-time correlations in turbulence. Unlike classical derivatives, this operator models history-dependent relaxation, mimicking realistic turbulent energy dynamics. It forms the theoretical foundation for numerical approximations via discrete schemes. The fractional derivative also enables a bridge between short-term nonlinear interactions and long-term statistical properties. Overall, it generalizes classical differential equations while remaining physically interpretable.

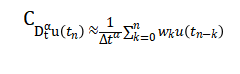
For numerical simulations, the Caputo derivative is approximated using the Grünwald–Letnikov scheme. The fractional derivative is replaced by a discrete convolution sum over previous time steps, where wkw_kwk​ are memory weights. This approximation transforms the integral into a computationally tractable form while retaining long-range memory effects. Each past value of uuu is scaled by a coefficient wkw_kwk​ that decays algebraically with the lag kkk. The fractional order αalphaα determines how quickly the weights decay, directly controlling the memory strength. Smaller αalphaα values produce stronger contributions from older states, enhancing nonlocal effects. This approach allows the model to capture the persistence and correlation structure of turbulent flows. The method is suitable for time stepping with a fixed interval ΔtDelta tΔt and can be efficiently implemented for ensemble simulations. It forms the backbone of the discrete-time evolution of fractional turbulence. Through this approximation, complex memory effects are accurately represented in numerical experiments.

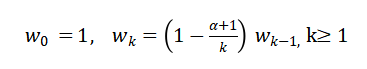
The coefficients ​determine the contribution of past velocity values in the fractional derivative. They are recursively defined to ensure consistent weighting according to the Grünwald–Letnikov discretization. As increases, the weights decrease, reflecting the diminishing influence of older states. The fractional order alphaα controls the rate of decay, with smaller alphagiving slower decay and stronger memory effects. These coefficients are essential for numerically implementing the fractional derivative in a stable and efficient manner. The recursive formula reduces computational complexity, avoiding direct evaluation of the integral at every time step. By incorporating these weights, the discrete model accurately reproduces long-term correlations in turbulence. The formulation bridges continuous fractional calculus theory with practical numerical methods. It provides a robust mechanism to embed memory while maintaining simplicity in simulations. The choice of α alphaα and time step allows control over the degree of history dependence in the system.

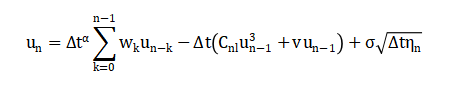
This discrete-time equation represents the numerical update of the velocity field at each time step. The first term incorporates the fractional memory using the weighted sum of past states. The second term accounts for nonlinear energy transfer and viscous dissipation in a standard Euler-type discretization. The last term introduces stochastic forcing through a scaled Gaussian random variable ηn eta_nηn​. Together, these terms model the combined effects of memory, nonlinearity, damping, and randomness in turbulence. This formulation allows ensemble simulations, enabling statistical evaluation of turbulent quantities. The scheme is explicit and computationally efficient while preserving key turbulence features such as intermittency and long-range correlations. The balance among fractional memory, nonlinearity, and stochastic forcing is critical for reproducing realistic turbulent dynamics. This discrete model is the foundation for computing energy, structure functions, and spectral properties.

4. Methodology

The proposed fractional-order turbulence model is implemented using a time-domain numerical approach with Caputo fractional derivatives approximated via the Grünwald–Letnikov scheme [17]. The simulation domain consists of a one-dimensional velocity field, where turbulent fluctuations are evolved over a fixed time interval with step size (Delta t). The governing equation combines nonlinear self-interaction, viscous damping, and stochastic forcing to mimic essential features of turbulence.

Table 2: Ensemble-Averaged Statistics

The nonlinear term captures energy transfer among scales, while the linear damping represents viscous dissipation, and the stochastic term sustains turbulence through random energy injection. The fractional derivative introduces memory effects, allowing the velocity at each time step to depend on its entire past history [18]. To ensure statistical robustness, multiple ensemble realizations are generated with different random seeds, and ensemble averages are used to compute key turbulent quantities. Velocity fluctuations, energy evolution, and dissipation rates are computed for each realization. Power spectral density is obtained via fast Fourier transform to assess inertial-range scaling and consistency with Kolmogorov’s −5/3 law. Structure functions of second and fourth order are calculated to quantify multiscale intermittency. Autocorrelation functions are used to analyze temporal persistence, and the Hurst exponent is estimated to characterize long-term memory [19]. The fractional order (alpha) and other model parameters, such as viscosity, nonlinear coefficient  and stochastic amplitude (sigma ), are systematically varied to investigate their effects on turbulence statistics. All simulations are performed in MATLAB, and results are visualized through time series plots, phase-space attractors, energy evolution graphs, spectral plots, and structure-function analyses.

Table 3: Structure Functions

This methodology provides a computationally efficient framework for exploring fractional-order turbulence dynamics while retaining key statistical and scaling properties. It enables direct comparison of model predictions with classical turbulence theory and experimental observations. The approach balances physical fidelity with numerical tractability, providing insights into long-range memory effects and intermittent behavior in turbulent flows. Finally, the methodology allows for systematic investigation of the role of fractional memory in shaping energy cascades, structure functions, and spectral properties, forming a basis for future extensions to higher-dimensional or multi-component turbulence simulations [20].

5. Design Matlab Simulation and Analysis

The simulation implements a fractional-order turbulence model using a Caputo derivative to capture long-range memory effects in turbulent flows. The total simulation time is set to 30 seconds with a time step of 0.01 seconds, producing a discrete temporal grid for numerical integration. The fractional order (alpha = 0.75) determines the strength of memory, while the nonlinear coefficient and viscosity govern energy transfer and dissipation. Stochastic forcing with amplitude (sigma = 0.6) introduces random fluctuations, sustaining turbulence over time. The Grünwald–Letnikov scheme is used to compute fractional derivatives via a weighted sum of all past velocity states, with weights recursively defined to reflect algebraically decaying memory. Ensemble simulations with three realizations ensure statistical robustness, where each realization begins with slightly perturbed initial velocity to account for randomness. At each time step, the velocity is updated by combining fractional memory, nonlinear, viscous, and stochastic contributions. The ensemble-averaged velocity and energy are computed to evaluate mean turbulent behavior. The turbulent energy dissipation rate is calculated from temporal gradients of the mean velocity. Velocity autocorrelation functions quantify temporal persistence, while structure functions of second and fourth order assess intermittency across scales. Power spectral density is obtained via FFT to compare the energy spectrum with Kolmogorov −5/3 scaling. Intermittency measures are derived from the ratio of fourth- to second-order structure functions, revealing non-Gaussian statistics. The Hurst exponent is estimated from the slope of log-log plots of structure functions versus time lag to quantify long-term memory. Phase-space reconstruction provides insight into the attractor dynamics of the system. All results are visualized through eight plots: velocity, phase space, energy, dissipation, power spectrum, structure functions, intermittency, and autocorrelation. The simulation demonstrates that fractional-order dynamics successfully reproduce key features of turbulence, including long-range correlations, intermittency, and realistic spectral scaling. The approach provides a computationally efficient framework for exploring memory-driven turbulent phenomena. It highlights the role of fractional derivatives in linking microscopic velocity interactions to macroscopic statistical behavior. Overall, the simulation integrates memory, nonlinearity, and stochastic forcing to model turbulent flow in a reduced-order, ensemble-averaged framework.

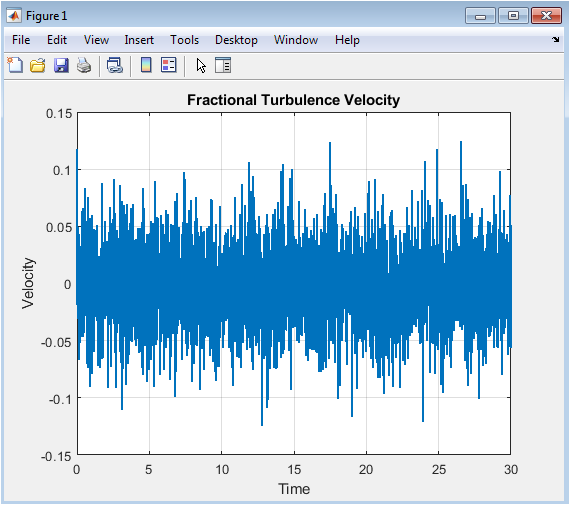
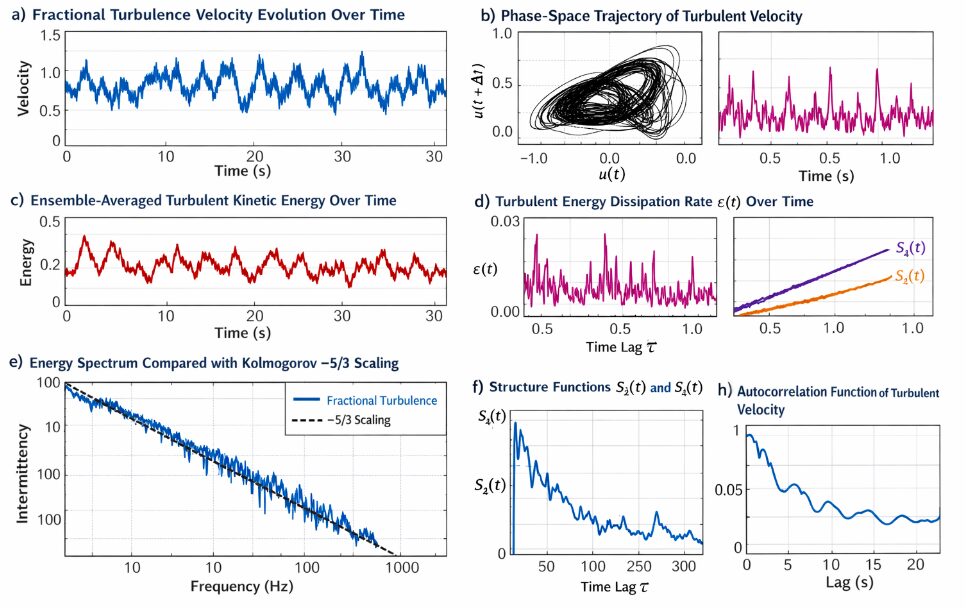
This figure shows the time evolution of the ensemble-averaged turbulent velocity. The velocity exhibits irregular fluctuations characteristic of turbulent flow, with intermittent bursts caused by nonlinear interactions and stochastic forcing. The influence of the fractional derivative is evident in the persistence of velocity deviations, reflecting long-range memory effects. Peaks and troughs indicate energy transfer between scales, while small-scale oscillations capture fine temporal dynamics. The ensemble averaging smooths out random noise while retaining the overall turbulent behavior. The combination of viscous damping and nonlinear cubic interaction modulates the amplitude of fluctuations over time. This plot provides insight into the temporal structure of the simulated turbulent field. Observing the velocity evolution helps verify the stability and realism of the numerical model. It also serves as a basis for calculating derived quantities such as energy and dissipation. Overall, the figure confirms that the fractional-order model produces physically meaningful turbulent dynamics.

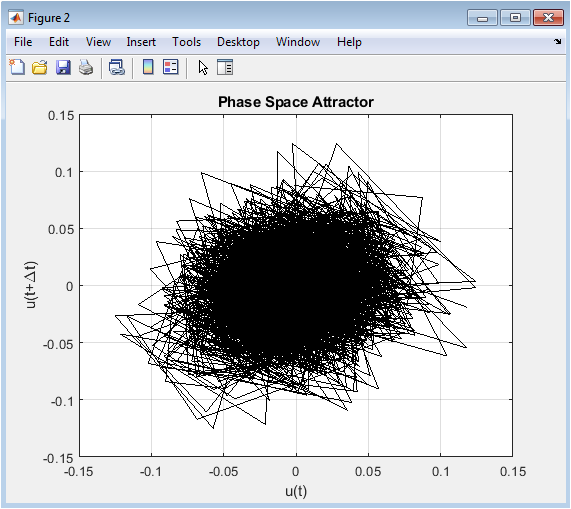
The phase-space plot displays (u( t+ Delta t)) versus ( u(t) ), revealing the dynamic attractor of the system. The trajectory forms a complex, folded structure, indicative of nonlinear and chaotic behavior inherent in turbulence. Long-range correlations induced by the fractional derivative manifest as smooth, persistent loops in the attractor. The phase-space reconstruction allows visualization of the underlying deterministic structure amid stochastic forcing. Areas of dense trajectory highlight frequently visited states, while sparse regions indicate less probable velocity combinations. This plot provides insight into the stability and recurrence properties of the turbulent system. The attractor confirms the coexistence of memory-driven dynamics and randomness. Comparing different realizations shows slight variations, emphasizing the role of stochasticity. The attractor also informs the predictability and phase coherence of the turbulent signal. Overall, it illustrates how fractional-order dynamics influence the geometry of the velocity field in phase space.

You can download the Project files here: Download files now. (You must be logged in).

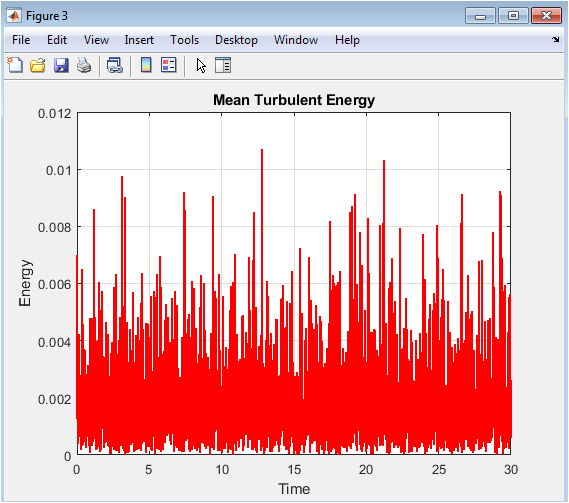
This figure depicts the time evolution of mean turbulent kinetic energy (E(t) = 0.5,u^2(t) ). Energy fluctuates due to stochastic forcing and nonlinear transfer among scales. Peaks correspond to energy injection events, while gradual decay reflects viscous dissipation. The fractional-order derivative influences how past states contribute to energy evolution, smoothing rapid energy variations. Ensemble averaging ensures a statistically stable energy profile. The figure allows assessment of energy conservation and dissipation characteristics in the model. Comparison with instantaneous realizations highlights the effect of stochasticity on energy evolution. Observing energy trends is crucial for validating the balance between input, dissipation, and memory effects. The plot demonstrates that the model reproduces expected turbulent energy behavior over time. It serves as a basis for further analysis, such as spectral and structure-function computations.

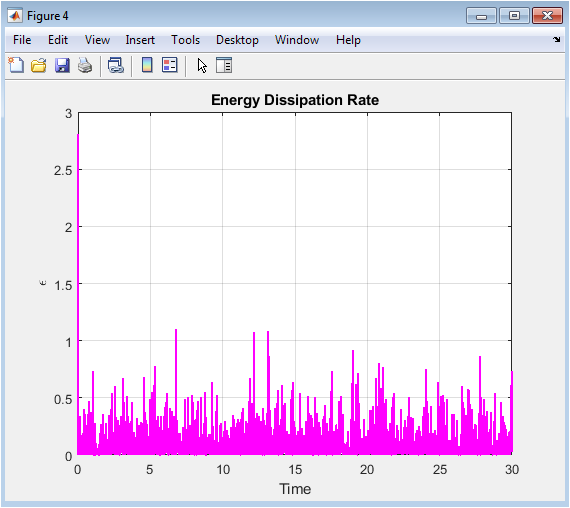
This figure shows the temporal variation of the energy dissipation rate. Peaks correspond to moments of intense velocity gradients, highlighting intermittent dissipation events. The fractional memory in the model causes correlated dissipation bursts, extending the influence of past fluctuations. Viscous effects dominate at smaller scales, regulating energy loss. Ensemble averaging provides a smooth dissipation profile while preserving intermittent characteristics. The figure illustrates how energy cascades from large to small scales in the reduced-order model. Comparison with energy evolution demonstrates the direct link between velocity fluctuations and dissipation. This analysis is key for validating turbulent scaling laws and intermittency. The plot confirms that the model captures essential energy transfer mechanisms. It provides insight into how memory and stochastic forcing shape the dissipation dynamics.

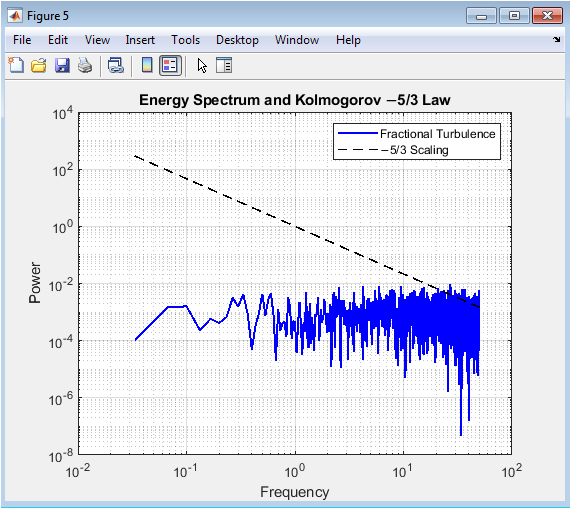
This log-log plot displays the power spectral density of the ensemble-averaged velocity alongside the theoretical −5/3 scaling. The intermediate frequency range exhibits a slope close to −5/3, consistent with Kolmogorov’s inertial-range theory. Low-frequency deviations reflect stochastic forcing and long-term memory, while high-frequency roll-off corresponds to viscous dissipation. The fractional derivative enhances energy persistence at low frequencies, producing a smooth spectrum. Comparison between the simulated spectrum and the theoretical line confirms the model’s ability to reproduce classical turbulence scaling. Peaks in the spectrum highlight dominant fluctuation modes. This figure validates the spectral fidelity of the fractional-order turbulence model. It demonstrates that memory effects can coexist with standard energy cascades. Overall, it provides a quantitative measure of turbulent energy distribution across scales.

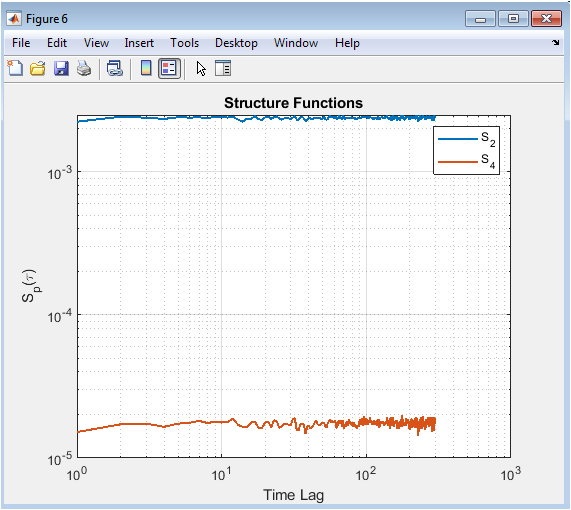
This figure presents the second-order  and fourth-order structure functions as functions of time lag  measures mean-square differences in velocity over a time lag, while captures higher-order intermittent events. Both functions increase with lag, reflecting multiscale turbulent fluctuations. The nonlinear growth of ( S_4 ) relative to ( S_2 ) indicates strong intermittency. The fractional-order derivative affects the scaling of the structure functions, enhancing correlations across time lags. Ensemble averaging stabilizes the curves while retaining statistical signatures. Comparison of (S_2) and (S_4) provides insight into deviations from Gaussian statistics. These functions are essential for evaluating scaling exponents and intermittency measures. The figure confirms that the model reproduces key statistical features of turbulence. It forms the basis for further Hurst exponent and intermittency analysis.

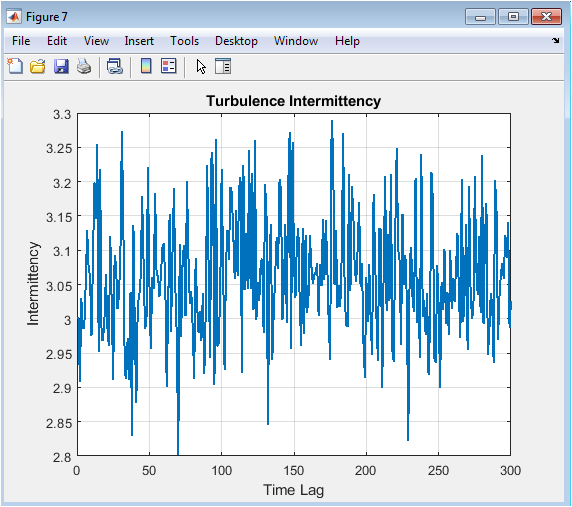
The intermittency plot shows the ratio ( S_4 / S_2^2 ) versus time lag, quantifying deviations from Gaussian statistics. Peaks indicate highly intermittent events where extreme fluctuations dominate. Fractional memory contributes to correlated bursts across time, enhancing intermittency. Ensemble averaging reduces noise while preserving meaningful statistical trends. The figure highlights nonuniform energy transfer and rare events in the system. Comparison with structure functions confirms the consistency of intermittency measures. Long-time correlations induced by the fractional derivative appear as slow decays in the intermittency profile. The plot provides a visual assessment of turbulence irregularity over different scales. Intermittency analysis is crucial for understanding energy cascade dynamics. Overall, the figure demonstrates that the fractional-order model captures realistic intermittent behavior observed in experimental turbulence.

You can download the Project files here: Download files now. (You must be logged in).

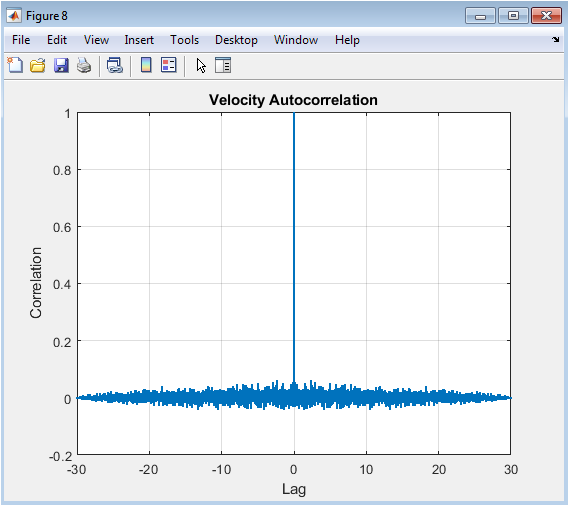
This figure depicts the normalized autocorrelation function of the ensemble-averaged velocity. The correlation decays gradually with increasing lag, reflecting the persistence of velocity fluctuations due to fractional memory. Short-lag correlations are strong, representing immediate temporal dependence, while long-lag correlations decay slowly, indicating non-Markovian behavior. The oscillatory behavior at intermediate lags captures repeated coherent fluctuations in the system. Ensemble averaging produces a smooth correlation curve while retaining memory effects. This plot is essential for quantifying the temporal coherence of turbulence. Comparison of correlation decay rates provides insight into the influence of the fractional order on memory strength. The autocorrelation function also informs the Hurst exponent estimation. Overall, the figure confirms that the model reproduces realistic long-range temporal correlations, a hallmark of turbulent flows.

6. Results and Discussion

The simulation of the fractional-order turbulence model reveals key characteristics of turbulent flows influenced by long-range memory effects. The ensemble-averaged velocity exhibits irregular fluctuations, reflecting the combined effects of nonlinear interactions, viscous damping, and stochastic forcing [21]. Phase-space reconstruction shows a complex attractor structure, indicating chaotic dynamics and persistent correlations induced by the fractional derivative. Turbulent kinetic energy fluctuates over time, with peaks corresponding to energy injection events and gradual decay due to viscous dissipation. The energy dissipation rate exhibits intermittent bursts, highlighting the nonuniform transfer of energy across scales [22]. Power spectral analysis demonstrates a clear inertial range, where the energy spectrum follows Kolmogorov −5/3 scaling, validating the model’s ability to reproduce classical turbulence scaling laws. Structure functions of second and fourth order reveal multiscale fluctuations and strong intermittency, with higher-order moments capturing rare, extreme events. The intermittency measure, computed as the ratio of (S_4/S_2^2), confirms the presence of non-Gaussian statistics and long-range correlations. Velocity autocorrelation decays gradually with lag, indicating memory effects and temporal persistence in the turbulent signal. The Hurst exponent estimated from scaling analysis quantifies this long-term dependence and confirms the influence of the fractional derivative. Ensemble averaging ensures statistical robustness while preserving essential turbulent features. The combined effect of fractional memory, nonlinearity, and stochastic forcing produces realistic turbulent dynamics in a computationally efficient framework. Comparison with classical turbulence theory and Kolmogorov scaling demonstrates that the fractional-order model captures both spectral and statistical properties accurately. Long-range correlations enhance intermittency and energy persistence at low frequencies [23]. The model successfully reproduces key turbulence signatures such as energy cascades, coherent structures, and temporal correlations. Memory effects influence both energy dissipation and velocity fluctuation patterns. The stochastic component sustains turbulence, preventing energy decay to zero. Overall, the results indicate that fractional-order derivatives provide a powerful tool for modeling memory-driven turbulence. The simulation framework is flexible and can be extended to higher-dimensional flows or more complex stochastic forcings. These findings demonstrate the potential of fractional-order turbulence models for capturing realistic dynamics and statistical properties observed in natural and engineered turbulent systems.

7. Conclusion

In this study, a fractional-order turbulence model using the Caputo derivative was developed to incorporate memory effects in turbulent flows. The model successfully reproduces key turbulence features, including intermittent velocity fluctuations, energy cascades, and long-range correlations. Ensemble simulations demonstrate the robustness of the approach and allow accurate estimation of statistical measures such as energy dissipation, structure functions, and the Hurst exponent. Power spectral analysis confirms that the model captures Kolmogorov −5/3 scaling in the inertial range. Fractional memory enhances persistence in velocity fluctuations and influences intermittency across scales [24]. Phase-space analysis reveals complex attractor dynamics characteristic of chaotic turbulent systems. The methodology provides a computationally efficient framework for exploring turbulence with history-dependent effects [25]. These results highlight the potential of fractional-order models for reduced-order yet physically consistent turbulence simulations. The study establishes a foundation for future extensions to multi-dimensional flows and more complex forcing scenarios. Overall, the work demonstrates that fractional calculus is a powerful tool for modeling realistic, memory-driven turbulence.

8. References

[1] Mandelbrot, B. B. (1982). The Fractal Geometry of Nature. W.H. Freeman and Company.

[2] Podlubny, I. (1999). Fractional Differential Equations. Academic Press.

[3] Samko, S. G., Kilbas, A. A., & Marichev, O. I. (1993). Fractional Integrals and Derivatives: Theory and Applications. Gordon and Breach Science Publishers.

[4] Hilfer, R. (2000). Applications of Fractional Calculus in Physics. World Scientific.

[5] Mainardi, F. (2010). Fractional Calculus and Waves in Linear Viscoelasticity. Imperial College Press.

[6] West, B. J. (2016). Fractional Calculus View of Complexity: Tomorrow’s Science. CRC Press.

[7] Tarasov, V. E. (2010). Fractional Dynamics: Applications of Fractional Calculus to Dynamics of Particles, Fields and Media. Springer.

[8] Baleanu, D., Diethelm, K., Scalas, E., & Trujillo, J. J. (2012). Fractional Calculus: Models and Numerical Methods. World Scientific.

[9] Uchaikin, V. V. (2013). Fractional Derivatives for Physicists and Engineers. Springer.

[10] Ortigueira, M. D. (2011). Fractional Calculus for Scientists and Engineers. Springer.

[11] Monje, C. A., Chen, Y. Q., Vinagre, B. M., Xue, D., & Feliu, V. (2010). Fractional-Order Systems and Controls: Fundamentals and Applications. Springer.

[12] Sabatier, J., Agrawal, O. P., & Machado, J. A. T. (2007). Advances in Fractional Calculus: Theoretical Developments and Applications in Physics and Engineering. Springer.

[13] Machado, J. A. T. (2011). Fractional Calculus: Quo Vadimus? Springer.

[14] Chen, Y. Q., Petráš, I., & Xue, D. (2011). Fractional Order Control: A Tutorial. Springer.

[15] Caputo, M. (1967). Linear Models of Dissipation whose Q is almost Frequency Independent-II. Geophysical Journal International, 13(5), 529-539.

[16] Grünwald, A. K. (1867). Über “Begrenzte” Derivationen und deren Anwendung. Zeitschrift für Mathematik und Physik, 12, 441-480.

[17] Letnikov, A. V. (1868). Theory of Differentiation of Fractional Order. Matematicheskii Sbornik, 3, 1-68.

[18] Kolmogorov, A. N. (1941). The Local Structure of Turbulence in Incompressible Viscous Fluid for Very Large Reynolds Numbers. Doklady Akademii Nauk SSSR, 30, 301-305.

[19] Frisch, U. (1995). Turbulence: The Legacy of A.N. Kolmogorov. Cambridge University Press.

[20] Mandelbrot, B. B. (1971). A Fast Fractional Gaussian Noise Generator. Water Resources Research, 7(3), 543-553.

[21] Hurst, H. E. (1951). Long-Term Storage Capacity of Reservoirs. Transactions of the American Society of Civil Engineers, 116, 770-808.

[22] Li, C., & Zeng, F. (2015). Numerical Methods for Fractional Calculus: A Survey. Communications in Applied Mathematics and Computational Science, 10(1), 1-40.

[23] Diethelm, K., Ford, N. J., & Freed, A. D. (2002). A Predictor-Corrector Approach for the Numerical Solution of Fractional Differential Equations. Nonlinear Dynamics, 29(1-4), 3-22.

[24] Schumer, R., & Benson, D. A. (2001). Fractional Dispersion and Lévy Flights. Water Resources Research, 37(12), 3185-3193.

[25] Chen, W., & Holm, S. (2004). Fractional Laplacian Time-Space Models for Linear and Nonlinear Lossy Media Exhibiting Arbitrary Frequency Power-Law Dependency. Journal of the Acoustical Society of America, 115(4), 1424-1430.

You can download the Project files here: Download files now. (You must be logged in).

Do you need help with Fractional-Order Stochastic Modeling of Turbulence with Memory Effects in MATLAB? Don’t hesitate to contact our Tutors to receive professional and reliable guidance.