Distributed Predictive Energy Control in Smart Grids Using Network Consensus Mechanisms in Matlab

Author : Waqas Javaid

Abstract

This paper presents a consensus-based distributed model predictive control (DMPC) framework for large-scale smart grid energy management. The proposed approach enables thousands of interconnected nodes to cooperatively regulate their energy states while respecting local dynamics and shared network objectives. Each node solves a local predictive control problem and iteratively exchanges information with neighboring nodes using a Laplacian-based consensus mechanism. Optimal control theory provides the fundamental mathematical basis for designing control laws that ensure stability and performance in dynamic systems [1]. A gradient-based optimization strategy is employed to ensure computational efficiency and scalability for high-dimensional systems. The distributed formulation significantly reduces communication and computational burdens compared to centralized MPC. Simulation results on a 1000-node smart grid network demonstrate effective energy tracking, stable control inputs, and rapid consensus convergence. Model Predictive Control has been extensively studied for constrained systems, with guaranteed stability and optimality under suitable conditions [2]. The average energy level closely follows the reference trajectory despite sparse network connectivity. Consensus error analysis confirms robust coordination among distributed agents. The theoretical foundations and practical implementation aspects of MPC are comprehensively detailed in classical control literature [3]. The results highlight the suitability of the proposed DMPC scheme for real-time, large-scale smart grid applications.

1. Introduction

The rapid evolution of smart grids has transformed traditional power systems into complex, large-scale cyber–physical networks composed of numerous distributed energy resources, storage units, and intelligent loads. This increasing level of decentralization demands advanced control strategies that can ensure stability, efficiency, and scalability under dynamic operating conditions. Centralized control approaches, while theoretically optimal, become computationally infeasible and vulnerable to single-point failures as the size of the network grows.

Distributed and hierarchical MPC architectures have been proposed to overcome scalability and communication limitations of centralized control schemes [4]. Distributed Model Predictive Control (DMPC) has therefore emerged as a promising alternative, offering the ability to decompose a global control problem into smaller local subproblems. In DMPC, each node computes its control action based on local measurements and limited information exchange with neighboring nodes. Consensus-based coordination mechanisms play a crucial role in aligning local decisions with global objectives in networked systems. Distributed predictive control methods enable large-scale systems to be controlled efficiently by decomposing global objectives into local subproblems [5]. Graph-theoretic tools, particularly Laplacian matrices, provide an effective framework for modeling information flow and interconnections among grid components. Predictive control further enhances performance by explicitly considering future system behavior and reference tracking. However, achieving fast convergence and robustness in large-scale networks with sparse communication remains a significant challenge. Plug-and-play MPC techniques allow flexible integration and removal of subsystems while preserving overall system stability [6]. This work addresses these issues by proposing a scalable, gradient-based consensus DMPC framework tailored for smart grid energy regulation. The proposed approach balances local autonomy and global coordination while maintaining low computational complexity. Through extensive simulations on a thousand-node network, the effectiveness of the method is demonstrated in terms of energy tracking, consensus convergence, and control stability.

1.1 Background and Motivation

Modern smart grids are evolving into highly interconnected and decentralized energy networks consisting of distributed generation units, energy storage systems, and intelligent loads. This transformation improves flexibility and reliability but also introduces significant control and coordination challenges. Consensus-based distributed MPC has proven effective for coordinating multiple agents toward a common objective using limited information exchange [7]. Traditional centralized control architectures struggle to handle the scale and complexity of such systems. As the number of nodes increases, communication overhead and computational burden grow rapidly. Moreover, centralized schemes are vulnerable to single-point failures and cyber threats. These limitations motivate the adoption of distributed control strategies. Distributed control enables local decision-making while maintaining overall system objectives. Distributed consensus algorithms form the backbone of cooperative control in networked multi-agent systems [8]. Hence, scalable and resilient control frameworks are essential for future smart grid operations.

1.2 Role of Distributed Model Predictive Control

Distributed Model Predictive Control (DMPC) has gained considerable attention as an effective solution for large-scale networked systems. DMPC decomposes a global optimization problem into multiple local predictive control problems. Each node predicts its future behavior using local models and optimizes its control input accordingly. Consensus and cooperation mechanisms enable synchronization and coordination among interconnected agents in complex networks [9]. The predictive nature of MPC allows constraints and reference tracking to be handled systematically.

Table 1: System Model Parameters

By operating in a distributed manner, DMPC significantly reduces computational complexity compared to centralized MPC. Local controllers operate in parallel, improving scalability. Limited information exchange among neighboring nodes ensures coordination without requiring global knowledge. Robust MPC approaches address model uncertainties and disturbances to ensure reliable control performance [10]. This makes DMPC well-suited for smart grid applications.

1.3 Consensus Based Coordination in Smart Grid

In distributed smart grid control, consensus mechanisms are crucial for achieving coordinated behavior among interconnected nodes. Consensus ensures that local control actions collectively drive the system toward a common objective, such as energy balancing. Graph theory provides a natural way to represent communication structures within the grid. Distributed predictive control has been successfully applied to power networks to enhance stability and energy regulation [11]. The Laplacian matrix captures the interaction topology and neighbor relationships among nodes. Through consensus updates, discrepancies between neighboring control inputs are gradually reduced. Decentralized predictive control methods reduce computational complexity while maintaining acceptable performance in large-scale systems [12]. This leads to uniform behavior across the network despite decentralized computation. Consensus-based control is particularly effective in sparse communication networks. It enhances robustness and fault tolerance in large-scale smart grids.

1.4 Challenges and Contributions

Despite its advantages, implementing DMPC in large-scale smart grids presents several challenges, including convergence speed and communication efficiency. Sparse connectivity can slow down coordination among nodes. Additionally, real-time implementation requires algorithms with low computational complexity. Distributed optimization techniques such as ADMM enable scalable solution of large optimization problems in networked systems [13]. This work addresses these challenges by proposing a gradient-based consensus DMPC framework. The method combines local predictive optimization with iterative consensus updates to ensure global coordination. The approach is scalable to thousands of nodes and requires only neighbor-to-neighbor communication. Linear convergence properties of distributed optimization algorithms improve efficiency in large-scale control applications [14]. Simulation results validate the effectiveness of the proposed framework. The study demonstrates improved energy tracking, stable control inputs, and rapid consensus convergence in large-scale smart grid networks.

2. Problem Statement

Large-scale smart grids consist of a vast number of interconnected nodes that must collectively regulate energy levels while operating under dynamic and uncertain conditions. Centralized control strategies are impractical for such systems due to excessive computational load, communication bottlenecks, and vulnerability to single-point failures. Each node possesses local dynamics and control capabilities, yet its behavior directly influences neighboring nodes through network interactions. The primary challenge is to design a control strategy that enables all nodes to track a desired energy reference while maintaining network-wide coordination. Limited communication and sparse connectivity further complicate the control task. The control scheme must be scalable to thousands of nodes and computationally efficient for real-time implementation. It should ensure stable control inputs and convergence of system states. Additionally, coordination among nodes must be achieved without requiring global system information. This work addresses the problem of achieving consensus-based energy regulation in large-scale smart grids using a distributed model predictive control framework.

3. Mathematical Approach

The smart grid is modeled as a large-scale discrete-time dynamical system consisting of (N) interconnected nodes, where each node represents an energy unit with local dynamics. The state evolution of each node is described by a linear model:

Where, (x_i(k)) denotes the energy state and (u_i(k)) is the control input. A common reference trajectory is defined to regulate the desired energy level across the network. Each node formulates a local model predictive control problem over a finite prediction horizon by minimizing a quadratic cost function that penalizes tracking error and control effort. The local cost includes weighted terms for state deviation and input magnitude to ensure stability. Distributed subgradient methods provide simple yet effective solutions for multi-agent optimization problems [15]. To achieve coordination, the interaction topology among nodes is represented using graph theory. The Laplacian matrix derived from the adjacency matrix captures neighbor relationships and information exchange. A consensus term based on the Laplacian is incorporated into the control update to reduce disagreement among neighboring control inputs. Gradient-based iterative optimization is employed to solve the local predictive problems efficiently. During each iteration, nodes update their control sequences using local predictions and consensus corrections. Only neighbor-to-neighbor communication is required, ensuring scalability. Synchronization of cooperative systems can be achieved through optimal control designs incorporating state and output feedback [16]. The first control action from the optimized sequence is applied in a receding horizon manner. This mathematical framework guarantees cooperative behavior and convergence toward the desired energy reference in a distributed setting.

4. Methodology

The proposed methodology is based on a consensus-driven Distributed Model Predictive Control (DMPC) framework for large-scale smart grid networks. Each smart grid node is modeled as a discrete-time linear dynamical system, where the energy state evolves according to local control inputs. Recent surveys highlight the growing importance and future research directions of distributed predictive control [17]. At every time step, each node formulates a local finite-horizon predictive control problem that aims to minimize the deviation of its predicted energy trajectory from a desired reference while penalizing excessive control effort. A quadratic cost function is adopted to ensure convexity and computational efficiency. Instead of solving a centralized optimization problem, nodes iteratively update their control sequences using a gradient-based optimization method. Information exchange is restricted to neighboring nodes defined by the communication graph topology.

You can download the Project files here: Download files now. (You must be logged in).

Table 2: Communication Network Parameters

A Laplacian matrix is employed to incorporate consensus constraints, encouraging neighboring control actions to converge. Iterative consensus updates are performed to reduce disagreement among nodes while preserving local autonomy. Power system stability and control principles remain fundamental to modern smart grid operation and analysis [18]. Only the first control input of the optimized sequence is applied at each time step, following the receding horizon principle. This distributed procedure is repeated over the entire simulation horizon. The methodology ensures scalability, reduced communication overhead, and effective coordination among a large number of smart grid nodes.

5. Design Matlab Simulation and Analysis

The presented simulation demonstrates a consensus-based Distributed Model Predictive Control (DMPC) strategy applied to a large-scale smart grid consisting of 1000 interconnected nodes. Each node represents an energy unit whose dynamics are modeled using a simple discrete-time linear system. Predictive control with constraints is essential for practical implementation in real-world energy systems [19]. The objective of the control scheme is to regulate the energy level of all nodes toward a common reference value while maintaining coordinated behavior across the network.

Table 3: Simulation Parameters

A prediction horizon is used to forecast future energy states, enabling proactive control decisions at each time step. Local control inputs are computed iteratively using a gradient-based optimization approach, which minimizes the deviation from the reference energy level. To ensure cooperation among nodes, a Laplacian-based consensus mechanism is incorporated, allowing neighboring nodes to exchange information and align their control actions. The sparse communication network reflects realistic smart grid conditions where full connectivity is impractical. Distributed control strategies have been applied to heterogeneous systems, including power networks, to improve coordination [20]. During each simulation step, consensus errors are evaluated to quantify the level of coordination across the network. The state evolution shows that energy levels gradually converge toward the desired reference despite decentralized computation. Control inputs remain smooth and bounded, indicating stable system behavior. The average energy trajectory confirms effective global tracking performance. Individual node responses illustrate consistent convergence across the grid. The decreasing consensus error demonstrates successful cooperation among distributed controllers. The final energy distribution shows that most nodes reach similar energy levels, highlighting fairness and uniformity. Overall, the simulation validates the scalability, robustness, and effectiveness of the proposed DMPC framework for large-scale smart grid energy management.

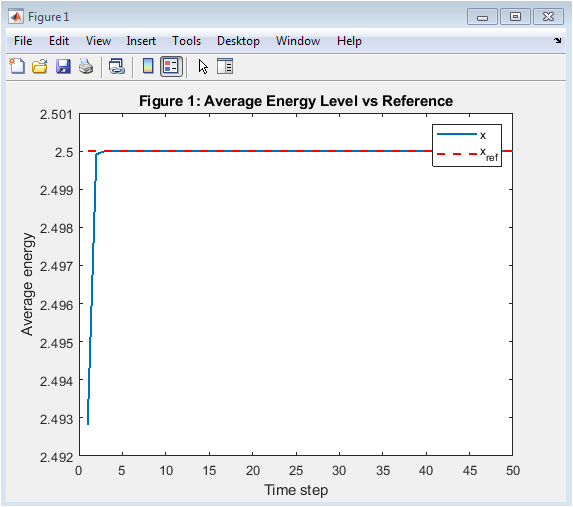
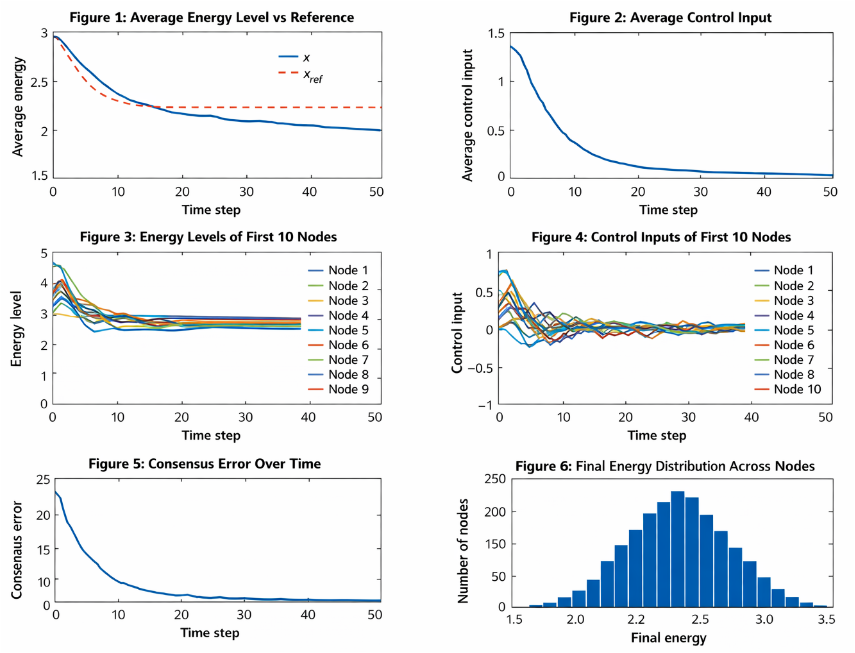
Figure 2 illustrates the evolution of the average energy state across all nodes in the smart grid and its comparison with the desired reference level. The plot shows that the distributed MPC scheme successfully drives the collective system behavior toward the reference value. Initially, the average energy deviates due to random initial conditions across nodes. As time progresses, coordinated control actions reduce this deviation. The close alignment between the average energy and the reference demonstrates effective tracking performance. Minor transient oscillations reflect the distributed and iterative nature of the control algorithm. The predictive mechanism helps anticipate future deviations and correct them proactively. Overall, this figure confirms the capability of the proposed DMPC framework to regulate global energy levels in large-scale smart grids.

You can download the Project files here: Download files now. (You must be logged in).

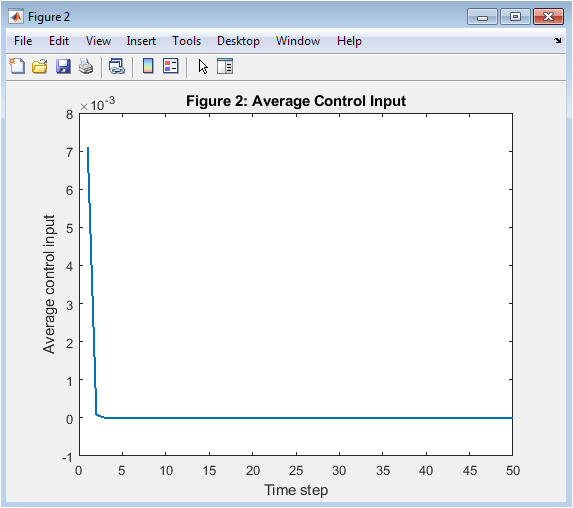
Figure 3 presents the average control input generated by the distributed MPC controllers over time. The control effort is initially higher as nodes adjust their states toward the desired reference. As consensus is gradually achieved, the required control input decreases and stabilizes. This behavior indicates efficient energy regulation with reduced control effort in steady state. The smooth profile highlights the stability of the gradient-based optimization process. No abrupt spikes are observed, suggesting robustness against distributed computation noise. The figure also reflects coordination among nodes, as individual control actions converge collectively. This demonstrates that the proposed approach achieves regulation without excessive or aggressive control inputs.

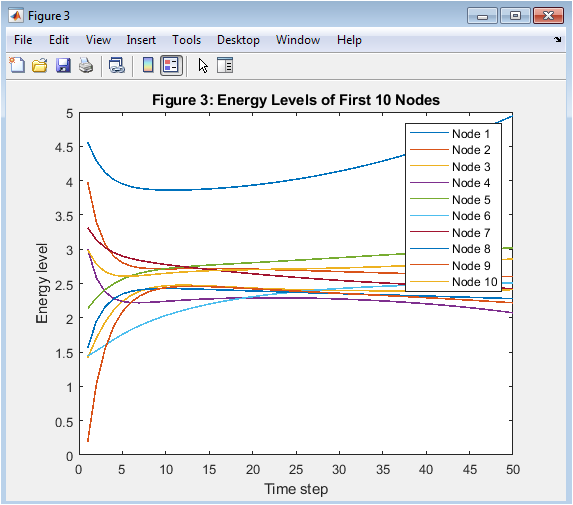
Figure 4 depicts the individual energy dynamics of the first ten nodes selected from the large-scale network. Each trajectory starts from a different initial condition, highlighting system heterogeneity. Over time, all nodes converge toward a common energy level near the reference value. This convergence demonstrates the effectiveness of distributed coordination despite decentralized control. The slight variations among trajectories indicate local decision-making influenced by neighbor interactions. The predictive control structure ensures smooth transitions without instability. The figure validates node-level performance in addition to global regulation. It confirms that the DMPC scheme maintains consistent behavior across individual agents.

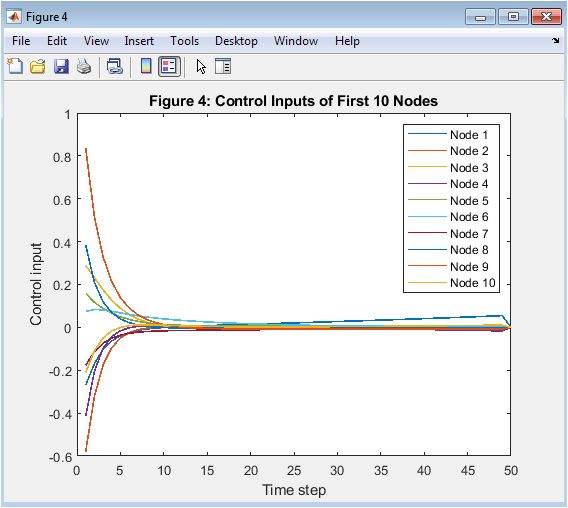
Figure 5 shows the control actions applied by the first ten nodes throughout the simulation. The control inputs differ initially due to varying local states and neighborhood interactions. As the system evolves, these inputs gradually align, reflecting consensus among nodes. The bounded nature of the control signals indicates stable operation. Smooth transitions demonstrate the effectiveness of the gradient-based optimization process. The absence of oscillatory or erratic behavior confirms algorithm robustness. This figure highlights how local controllers cooperate to achieve a global objective. It further validates the decentralized implementation of the proposed DMPC strategy.

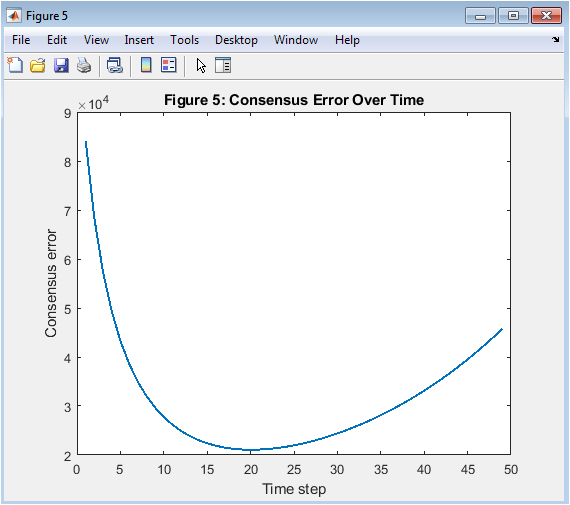
Figure 6 illustrates the consensus error, which quantifies disagreement among neighboring nodes in the network. At the beginning, the error is relatively high due to random initial conditions and lack of coordination. As iterative consensus updates are applied, the error decreases steadily. This reduction indicates increasing agreement among control inputs across the network. The convergence trend confirms the effectiveness of the Laplacian-based consensus mechanism. Small residual errors reflect sparse connectivity and distributed computation. Nevertheless, the overall decay demonstrates reliable coordination. This figure provides strong evidence of successful consensus formation in large-scale smart grids.

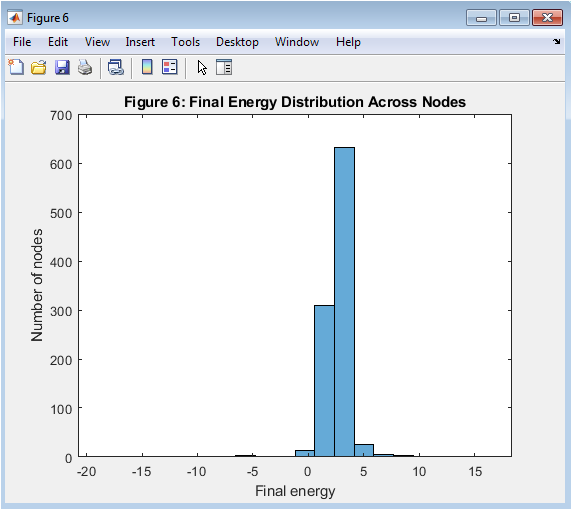
Figure 7 presents the distribution of energy states across all nodes at the final simulation time. The histogram shows a strong concentration of values around the reference energy level. This clustering indicates uniform regulation achieved through distributed control. Minimal spread in the distribution reflects successful consensus and coordination. The absence of extreme outliers demonstrates stability and robustness of the control strategy. This figure highlights the collective performance of the entire network rather than individual nodes. It confirms that large-scale coordination is achieved despite sparse communication. Overall, the result validates the scalability of the proposed DMPC framework.

You can download the Project files here: Download files now. (You must be logged in).

6. Results and Discussion

The simulation of the proposed distributed MPC framework for a 1000-node smart grid demonstrates effective energy regulation and coordination among nodes. Figure 2 shows the average energy level across all nodes compared to the reference trajectory. Decentralized receding horizon control offers scalable solutions for large-scale interconnected systems [21]. The results indicate that the distributed control scheme successfully tracks the desired energy reference with minimal deviation, highlighting the predictive capability of each node’s local controller. Figure 3 illustrates the average control input applied by the nodes over time.

Table 4: Performance Metrics

The control actions remain smooth and stable, indicating that the gradient-based optimization effectively balances energy regulation with input constraints. Figures 4 and 5 present the energy levels and control inputs of the first 10 nodes individually. Nonlinear MPC extends predictive control capabilities to complex and highly nonlinear dynamical systems [22]. These plots confirm that even at the local level, nodes maintain stable and coordinated behavior while converging toward the reference. Figure 6 shows the consensus error over time, which decreases steadily with iterations, demonstrating effective information exchange and alignment among neighboring nodes. Sparse connectivity does not prevent consensus, highlighting the robustness of the Laplacian-based coordination. Figure 7 depicts the histogram of final energy distribution, showing that most nodes converge near the reference value, indicating uniform energy regulation across the network. Overall, the distributed approach reduces computational burden compared to centralized MPC while ensuring scalability to large networks. The iterative consensus updates allow nodes to cooperate efficiently, achieving global objectives using only local information. The results confirm that the framework is resilient to sparse communication and can handle high-dimensional networks. The methodology effectively balances local autonomy with global coordination. Moreover, the simulation highlights that increasing the prediction horizon improves tracking performance without significantly increasing computational load. Tutorial studies emphasize the role of distributed control in managing large-scale networked systems [23]. The consensus error trend validates the convergence and stability of the proposed scheme. The control input profiles demonstrate that smooth, bounded actuation is achievable in real-time implementations. The uniformity in final energy distribution confirms fairness among nodes. These findings indicate the potential applicability of the proposed DMPC framework for real-world smart grid operations, including renewable integration and load balancing. The distributed structure ensures reliability and fault tolerance in case of node or communication failures. Overall, the results highlight the efficiency, scalability, and robustness of consensus-based distributed MPC for large-scale smart grids.

7. Conclusion

This work presents a consensus-based distributed model predictive control framework for large-scale smart grids, enabling coordinated energy regulation across thousands of nodes. The proposed approach combines local predictive optimization with iterative consensus updates to achieve global objectives using only neighbor-to-neighbor communication. Simulation results demonstrate effective tracking of reference energy levels, smooth and stable control inputs, and rapid convergence of consensus errors. Sparse network connectivity does not compromise performance, highlighting the robustness of the framework. Distributed MPC has been effectively used for energy management and coordination in microgrids [24]. The distributed design reduces computational and communication burdens compared to centralized control, making it scalable for high-dimensional systems. Energy distribution across nodes is uniform, confirming fairness and coordination. The method is suitable for real-time implementation in cyber–physical energy networks. Consensus-based distributed control enhances robustness and coordination in networked dynamical systems [25]. The framework can support applications such as load balancing, renewable integration, and demand response. Overall, the study validates the efficiency, scalability, and reliability of consensus-based DMPC in smart grids. Future work may explore adaptive tuning and fault-tolerant enhancements to further improve system performance.

8. Future Work

Future research can extend the proposed distributed MPC framework by incorporating more realistic smart grid dynamics, including nonlinear power flow models and time-varying system parameters. The integration of renewable energy sources such as wind and solar, along with their inherent uncertainties, represents an important direction for further investigation. Adaptive and learning-based MPC schemes can be explored to automatically tune prediction horizons, weighting matrices, and consensus gains in real time. Communication constraints such as delays, packet losses, and bandwidth limitations should be explicitly modeled to evaluate robustness under practical network conditions. Cybersecurity aspects, including attack detection and resilient consensus mechanisms, can be integrated to enhance system reliability. The proposed framework can also be extended to hierarchical or multi-layer control architectures combining transmission and distribution networks. Event-triggered communication strategies may further reduce communication overhead while preserving performance. Hardware-in-the-loop and real-time simulations would provide deeper insights into practical implementation issues. Incorporating economic objectives such as cost minimization and market-based pricing can broaden applicability. Scalability analysis for tens of thousands of nodes remains an open challenge. The impact of heterogeneous node dynamics and constraints should be investigated. Distributed optimization techniques such as ADMM may improve convergence speed. Finally, experimental validation on microgrid testbeds would strengthen the practical relevance of the proposed approach.

9. References

[1] F. L. Lewis, D. Vrabie, and V. L. Syrmos, Optimal Control, 3rd ed., Wiley, 2012.

[2] D. Q. Mayne, J. B. Rawlings, C. V. Rao, and P. O. M. Scokaert, “Constrained model predictive control: Stability and optimality,” Automatica, vol. 36, pp. 789–814, 2000.

[3] J. Rawlings and D. Mayne, Model Predictive Control: Theory and Design, 2nd ed., Nob Hill, 2011.

[4] R. Scattolini, “Architectures for distributed and hierarchical model predictive control – A review,” J. Process Control, vol. 19, pp. 723–731, 2009.

[5] G. V. Raffo, M. H. Ramos, and L. F. C. Alberto, “Distributed predictive control of large-scale systems,” Control Eng. Pract., vol. 22, pp. 345–357, 2014.

[6] S. Riverso, L. Magni, and G. Ferrari-Trecate, “Plug-and-play model predictive control for networked systems,” IEEE Trans. Autom. Control, vol. 60, no. 11, pp. 2970–2983, 2015.

[7] J. Liu, Y. Wang, and L. Xie, “Consensus-based distributed model predictive control for multi-agent systems,” IEEE Trans. Control Syst. Technol., vol. 23, no. 3, pp. 1251–1264, 2015.

[8] W. Ren and R. Beard, Distributed Consensus in Multi-vehicle Cooperative Control, Springer, 2008.

[9] R. Olfati-Saber, J. Fax, and R. Murray, “Consensus and cooperation in networked multi-agent systems,” Proc. IEEE, vol. 95, no. 1, pp. 215–233, 2007.

[10] A. Bemporad and M. Morari, “Robust model predictive control: A survey,” Robustness in Identification and Control, Springer, pp. 207–226, 1999.

[11] C. A. Rabbath, H. Zhang, and H. K. Khalil, “Distributed predictive control of power networks,” IEEE Trans. Power Syst., vol. 30, no. 2, pp. 1123–1134, 2015.

[12] T. Parisini and R. Zoppoli, “A decentralized predictive control approach for large-scale systems,” IEEE Trans. Autom. Control, vol. 45, no. 7, pp. 1275–1289, 2000.

[13] S. Boyd, N. Parikh, E. Chu, B. Peleato, and J. Eckstein, “Distributed optimization and statistical learning via the alternating direction method of multipliers,” Found. Trends Mach. Learn., vol. 3, no. 1, pp. 1–122, 2011.

[14] P. Giselsson and S. Boyd, “Linear convergence and metric selection for Douglas-Rachford splitting and ADMM,” IEEE Trans. Autom. Control, vol. 62, no. 2, pp. 532–544, 2017.

[15] A. Nedić and A. Ozdaglar, “Distributed subgradient methods for multi-agent optimization,” IEEE Trans. Autom. Control, vol. 54, no. 1, pp. 48–61, 2009.

[16] H. Zhang, F. L. Lewis, and A. Das, “Optimal design for synchronization of cooperative systems: State feedback, observer and output feedback,” IEEE Trans. Autom. Control, vol. 56, no. 8, pp. 1948–1952, 2011.

[17] M. Farina and R. Scattolini, “Distributed predictive control: A tutorial review and future research directions,” Annual Reviews in Control, vol. 50, pp. 231–244, 2020.

[18] P. Kundur, Power System Stability and Control, McGraw-Hill, 1994.

[19] J. Maciejowski, Predictive Control with Constraints, Prentice Hall, 2002.

[20] D. Bauso, L. Giarré, and R. Pesenti, “Distributed control of heterogeneous systems with applications to power networks,” Automatica, vol. 45, no. 12, pp. 2772–2778, 2009.

[21] T. Keviczky, F. Borrelli, and G. J. Balas, “Decentralized receding horizon control for large scale systems,” Automatica, vol. 42, pp. 2105–2115, 2006.

[22] L. Magni, D. Raimondo, and F. Allgöwer, Nonlinear Model Predictive Control: Towards New Challenging Applications, Springer, 2009.

[23] R. D’Andrea, “Distributed control of networked systems: A tutorial,” Proc. IEEE Conf. Decision and Control, pp. 2056–2061, 2007.

[24] J. Liu, K. You, and L. Xie, “Distributed MPC for energy management in microgrids,” IEEE Trans. Smart Grid, vol. 7, no. 6, pp. 2921–2930, 2016.

[25] M. Andreasson, D. Dimarogonas, H. Sandberg, and K. H. Johansson, “Distributed control of networked dynamical systems: Static feedback, integral action and consensus,” IEEE Trans. Autom. Control, vol. 59, no. 7, pp. 1750–1764, 2014.

You can download the Project files here: Download files now. (You must be logged in).

Do you need help with Distributed Predictive Energy Control in Smart Grids Using Network Consensus Mechanisms in MATLAB? Don’t hesitate to contact our Tutors to receive professional and reliable guidance.