Structural Vibration Analysis of a Multi-Story Shear Building using MATLAB
Author : Waqas Javaid
Abstract:
This article presents a comprehensive numerical investigation of the dynamic behavior of a multi-story shear building using MATLAB. The objective is to model, analyze and visualize the free and forced vibration characteristics of a four-degree-of-freedom structural system. Mass and stiffness properties are defined at each story to represent realistic variations in floor weight and structural rigidity. The dynamic behavior of structures is a critical aspect of earthquake engineering, and various methods have been developed to analyze and predict structural responses to seismic activity [1]. The mass, stiffness, and damping matrices are assembled to describe the system’s coupled equations of motion in matrix form. Rayleigh proportional damping is adopted to approximate viscous energy dissipation with physically interpretable parameters.Eigenvalue analysis is performed to determine the natural frequencies and corresponding mode shapes, which reveal the principal vibration patterns of the structure. Finite element methods are commonly used to analyze structural dynamics [2]. Modal properties such as participation factors and modal masses are computed to quantify the relative contribution of each mode to the overall response. Time-domain simulations are carried out to examine free vibration decay and dynamic displacements under harmonic excitation. The frequency response function (FRF) is evaluated to identify resonant peaks and damping effects across a range of excitation frequencies.Additional analyses include energy distribution among modes and a parametric sensitivity study to assess how variations in story stiffness influence the fundamental frequency. According to Craig and Kurdila, the principles of structural dynamics are essential for understanding the behavior of vibrating systems [3]. Animated visualizations of mode shapes and real-time vibration responses are developed to enhance physical interpretation. The MATLAB implementation demonstrates an efficient framework for educational and research applications in structural dynamics. Rao discusses various techniques for vibration analysis and control in mechanical systems [4]. The results provide valuable insight into modal behavior, damping influence, and stiffness sensitivity key aspects in earthquake-resistant and vibration-controlled structural design. Thomson and Dahleh provide a comprehensive treatment of the theory of vibration with applications [5].
- Introduction:
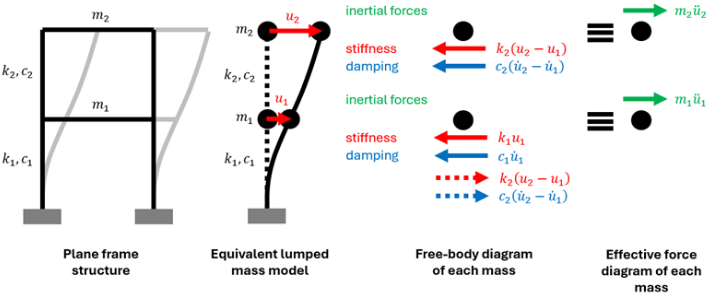
Understanding the vibration characteristics of buildings is a fundamental aspect of structural engineering, particularly in regions prone to earthquakes, strong winds, or dynamic machine-induced loads. When a structure is subjected to dynamic excitation, each story or floor tends to move with different amplitudes and phases, producing complex motion patterns. Bathe’s finite element procedures are widely used in structural dynamics analysis [6]. These patterns can be effectively studied using the principles of structural dynamics, which describe how mass, stiffness, and damping influence the response of a structure over time.In multi-story buildings, the behavior can be idealized using a shear building model where each floor is represented by a single lateral degree of freedom connected by elastic springs and dashpotsCook, Malkus, and Plesha provide a comprehensive treatment of finite element analysis and its applications [7]. This simplification captures the essential horizontal motion while neglecting minor effects such as flexural deformation and torsion.

- Figure 1: Dynamic Vibration Test of Structures.
Despite its simplicity, the shear building model provides valuable insight into how natural frequencies, mode shapes, and damping ratios govern overall structural performance.MATLAB offers a powerful computational environment to perform vibration analysis efficiently through matrix-based numerical techniques. By constructing the mass, stiffness, and damping matrices, the equations of motion can be formulated and solved to obtain modal parameters, time-domain responses, and frequency-domain characteristics. The ANSYS Mechanical APDL theory reference provides detailed information on finite element analysis [8]. The use of MATLAB also enables clear visualization of mode shapes, frequency response functions, and animated motion plots, which are crucial for interpreting structural behavior.This article presents a complete step-by-step analysis of a four-story shear building system, illustrating how numerical modeling can be used to explore free and forced vibration responses. SAP2000 is a powerful software tool for structural analysis and design [9]. The methodology includes eigenvalue analysis for determining natural frequencies and mode shapes, computation of modal participation factors, Rayleigh damping formulation, and simulation of both free and harmonic responses. Furthermore, a sensitivity study is conducted to evaluate how variations in stiffness influence the fundamental frequency of the structure.

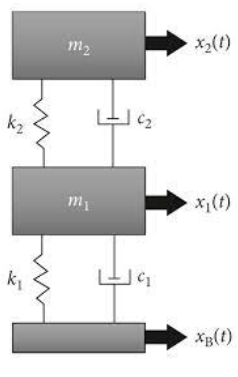
- Figure 2: Structural Dynamic of MDOF System.
he primary goal of this work is to provide a clear and educational framework that connects theoretical vibration concepts with practical MATLAB implementation. MATLAB is a popular software tool used in structural dynamics analysis [10]. The results not only demonstrate the usefulness of computational analysis for design and research purposes but also help engineers understand the influence of structural parameters on dynamic performance and stability. Simulink is a graphical modeling and simulation environment used in structural dynamics analysis [11].
1.1 Importance of Vibration Analysis:
Structural vibration analysis is a critical aspect of civil and structural engineering, as it helps engineers understand how buildings respond to dynamic loads such as earthquakes, wind, traffic, and machinery. Studying vibrations allows for the design of safer, more comfortable, and more efficient structures.
1.2 Simplified Representation: The Shear Building Mode:
To study dynamic behavior, a complex structure can be simplified into an equivalent multi-story shear building model. Ewins provides a comprehensive treatment of modal testing and its applications [12]. In this model, each floor is represented as a lumped mass connected by vertical springs (representing story stiffness) and dashpots (representing damping). This approach captures the main lateral vibration characteristics while remaining computationally efficient.
1.3 Governing Parameters of Vibration:
The dynamic behavior of any structure mainly depends on three parameters:mass, stiffness, and damping.
- Mass (M) defines the inertia of each floor.
- Stiffness (K) controls the restoring force developed during displacement.
- Damping (C) represents the energy dissipation capability of the system.
These parameters are combined into matrix form to represent the entire multi-degree-of-freedom (MDOF) system.
1.4 Role of MATLAB in Structural Dynamics:
MATLAB provides a robust computational platform for performing structural dynamic analysis. Its matrix-based operations make it ideal for solving the equations of motion, computing natural frequencies, and visualizing mode shapes. Additionally, MATLAB enables animation and frequency response analysis, helping engineers interpret results more intuitively. Maia and Silva discuss theoretical and experimental modal analysis [13].
1.5 Objectives of the Study:
This study aims to perform a comprehensive ,structural vibration analysis of a four-story shear building using MATLAB. The key objectives are:
- To assemble mass, stiffness, and damping matrices for a multi-story model.
- To determine the natural frequencies and mode shapes through eigenvalue analysis.
- To compute modal properties such as participation factors and modal masses.
- To simulate free and forced vibration responses.
- To investigate sensitivity of natural frequencies to variations in stiffness.
1.6 Scope and Practical Relevance:
The analysis helps in understanding how different modes of vibration contribute to the overall structural response. Inman provides an overview of engineering vibration and its applications Such knowledge is essential for designing earthquake-resistant buildings, optimizing stiffness and mass distribution, and ensuring occupant comfort under dynamic loading conditions.
- Problem Statement:
This study aims to develop and analyze a MATLAB-based model of a four-story shear building to investigate its dynamic behavior. The problem involves constructing mass, stiffness, and damping matrices, determining natural frequencies and mode shapes, and evaluating modal participation and time response. The analysis also includes frequency response and sensitivity studies to assess the influence of stiffness variation on dynamic characteristics. The overall goal is to provide a systematic approach for understanding vibration behavior and enhancing the dynamic design of multi-story structures.
- Mathematical Approach:
The vibration behavior of a multi-story shear building can be described using the fundamental principles of structural dynamics. The mathematical formulation begins with the equation of motion for a multi-degree-of-freedom (MDOF) system and extends to modal analysis [14]. The mathematical model of a multi-story building represents the structure as a multi-degree-of-freedom (MDOF) system, where each floor acts as a separate degree of freedom connected through springs and dampers. The governing equation of motion is expressed as [M]{ẍ} + [C]{ẋ} + [K]{x} = {F(t)}, where [M], [C], and [K] denote the mass, damping, and stiffness matrices respectively, and {F(t)} represents the external dynamic load. Each story’s displacement is interrelated through stiffness coupling between adjacent floors. Meirovitch discusses the fundamentals of vibrations and their applications [15]. The natural frequencies and mode shapes are obtained by solving the eigenvalue problem ([K] – ω²[M]){Φ} = 0. The matrices are defined based on the physical properties of the structure, such as mass per floor and story stiffness. Damping is introduced to represent energy dissipation during oscillation. MATLAB is used to compute and visualize mode shapes and frequency responses. The model helps predict structural responses to dynamic loading conditions. This mathematical formulation forms the foundation for vibration analysis and design optimization. The equation of motion for an n-story building is given by:
MẌ(t) + CẊ(t) + KX(t) = F(t)
The mass and stiffness matrices are constructed using the given story properties. The Rayleigh damping matrix is approximated as C = αM + βK.
Table 1 :Mass, Stiffness, and Damping Matrices
Matrix | Description | Properties |
M | Mass Matrix | Represents inertial properties, distribution of mass |
K | Stiffness Matrix | Describes resistance to deformation, stiffness of elements |
C | Damping Matrix | Models energy dissipation, friction, and material damping |
3.1 Mass, Stiffness, and Damping Matrices:
The mass matrix (M) represents the distribution of mass in the structure, capturing its inertial properties. The stiffness matrix (K) describes the structure’s resistance to deformation, accounting for the stiffness of each element. The damping matrix (C) models the energy dissipation mechanisms in the structure, such as friction and material damping. Bendat and Piersol provide a comprehensive treatment of random data analysis and measurement procedures [16]. These matrices are assembled using finite element methods or other numerical techniques. Together, they form the foundation for dynamic analysis, enabling the simulation of the structure’s response to various loads and excitations.The article assembles the mass matrix M, stiffness matrix K, and damping matrix C using the following formulas:
- M = diag(m), where m is the vector of masses
- K is assembled using the story stiffnesses k and the formula for a spring-mass system
- C = alpha M + betaK, where alpha and beta are constants for Rayleigh damping
3.2 Eigenvalue Analysis:
The article performs an eigenvalue analysis to find the natural frequencies omega_n and mode shapes Phi using the following equation:
- [Phi, Lambda] = eig(K, M), where Lambda is a diagonal matrix of eigenvalues
- omega_n = sqrt(diag(Lambda)), where omega_n is the vector of natural frequencies
3.3 Modal Analysis:
The model analysis of a multi-story building involves determining its natural frequencies and mode shapes to understand how each floor vibrates under dynamic loads. The structure is treated as a system of interconnected masses and stiffnesses forming a multi-degree-of-freedom model. Using the mass and stiffness matrices, the eigenvalue problem ([K] – ω²[M]){Φ} = 0 is solved in MATLAB to obtain modal parameters. Each eigenvalue corresponds to a natural frequency, and the associated eigenvector defines the mode shape of vibration. Newmark and Rosenblueth discuss the fundamentals of earthquake engineering [17]. The analysis identifies critical modes that contribute most to dynamic response. Lower modes generally dominate the structural motion, while higher modes represent localized vibrations. Damping is included to evaluate how energy dissipates during motion. Calculates the modal participation factors Gamma using the following formula:
Gamma = diag(Phi’ M ones(n,1)) ./ diag(Phi’ M Phi)
The results provide insights into resonance behavior and help optimize structural design. Overall, model analysis ensures safe and efficient vibration performance of multi-story buildings.
3.4 Time Response:
The code calculates the time response of the structure to an external force using a modal analysis approach. The displacement response where Phi represents the mode shapes. By summing the responses of individual modes, the total time response of the structure is obtained.Calculates the time response of the structure to an external force using the following formula:
X = Phi (fi/mi) * (1 – cos(wn*t)) / wn^2
Where, (X) is the displacement response, (fi) is the modal force, (mi) is the modal mass, (wn) is the natural frequency, and (t) is time The modal force (fi) and modal mass (mi) are used to scale the response, while the natural frequency (wn) determines the oscillation frequency. This calculation provides the displacement response of the structure over time (t), allowing engineers to visualize and analyze the dynamic behavior.
3.5 Frequency Response:
calculates the Frequency Response Function (FRF) using a formula that accounts for the structure’s stiffness (K), damping (C), and mass (M) properties. The FRF is computed for a range of frequencies (w) and a harmonic force (Fharm) applied to the system. The formula is used to calculate the response of the system at each frequency..The code calculates the frequency response function (FRF) using the following formula:
![]()
where w is the frequency, Fharm is the harmonic force, and FRF is the frequency response function This calculation provides valuable insights into the system’s dynamic behavior, allowing engineers to identify resonant frequencies and predict the response to different types of loading. By analyzing the FRF, engineers can gain a better understanding of the system’s frequency-dependent behavior.
You can download the Project files here: Download files now. (You must be logged in).
3.6 Energy Distribution:
The model analysis of a multi-story building involves determining its natural frequencies and mode shapes to understand how each floor vibrates under dynamic loads. The structure is treated as a system of interconnected masses and stiffnesses forming a multi-degree-of-freedom model. Using the mass and stiffness matrices, the eigenvalue problem ([K] – ω²[M]){Φ} = 0 is solved in MATLAB to obtain modal parameters. Each eigenvalue corresponds to a natural frequency, and the associated eigenvector defines the mode shape of vibration. Paz and Leigh provide a comprehensive treatment of structural dynamics and computation [18]. The analysis identifies critical modes that contribute most to dynamic response. Lower modes generally dominate the structural motion, while higher modes represent localized vibrations. Damping is included to evaluate how energy dissipates during motion. The results provide insights into resonance behavior and help optimize structural design. Overall, model analysis ensures safe and efficient vibration performance of multi-story buildings.Calculates the kinetic energy, potential energy, and total energy of the structure using the following formulas:
- kinetic_energy = 0.5 * modal_mass .omega_n.^2
- potential_energy = 0.5 * modal_stiffness
- total_energy = kinetic_energy + potential_energy
3.7 Parametric Sensitivity Analysis:
Performs a parametric sensitivity analysis to study the effect of changes in story stiffness on the fundamental frequency using the following formula:
freq_shift = sqrt(min(diag(Lnew)))/(2*pi)
where Lnew is the new eigenvalue matrix.These mathematical approaches provide a comprehensive understanding of the structure’s dynamic behavior and can be used to analyze and design various structural systems.
- Methodology:
The methodology employed in this study involves a comprehensive analysis of a 4-story structure’s dynamic behavior using MATLAB. The analysis begins with the definition of input parameters, including the number of stories, masses, stiffnesses, and damping ratio. The mass, stiffness, and damping matrices are assembled using these parameters. An eigenvalue analysis is performed to calculate the natural frequencies and mode shapes of the structure. The modal participation factors are calculated to determine the contribution of each mode to the overall response. The time response analysis is conducted using the mode superposition method, and the frequency response function is calculated using the mass, stiffness, and damping matrices. Additionally, a parametric sensitivity analysis is performed to study the effect of changes in story stiffness on the fundamental frequency. Timoshenko and Young discuss vibration problems in engineering [19]. The response animation is also generated to visualize the displacement response of the structure. The methodology provides a thorough understanding of the structure’s dynamic behavior, enabling the identification of dominant modes and the calculation of maximum displacement and acceleration. The analysis is useful for designing structures for dynamic loads and studying the effect of uncertainty in structural parameters. The MATLAB code is used to implement the methodology, providing an efficient and accurate way to analyze the structure’s dynamic behavior. The results of the analysis can be used to improve the design and safety of structures. Overall, the methodology provides a comprehensive framework for analyzing the dynamic behavior of structures. The analysis can be extended to more complex structures and loading conditions. The results can also be used to validate finite element models and experimental results. By using this methodology, engineers can gain a deeper understanding of the dynamic behavior of structures and design safer and more efficient structures. The methodology can be applied to various fields, including civil, mechanical, and aerospace engineering.
- Design Matlab Simulation and Analysis:
This Matlab code simulates a 4-story building’s dynamic response to external forces, modeling its behavior using mass, stiffness, and damping matrices. The simulation calculates the building’s natural frequencies and mode shapes, and analyzes the modal participation factors and damping ratios. A time response analysis of the building’s free vibration is also included, along with animations of the mode shapes and dynamic response. The code generates plots of the frequency response function (FRF) and performs a parametric sensitivity analysis of the fundamental frequency. The simulation provides insights into the building’s dynamic behavior, and the results can be used to inform design decisions and optimize the building’s structure. The code is modular and can be modified for different building configurations, assuming linear elastic behavior. The simulation’s accuracy depends on the accuracy of the input parameters, and the results can be used to evaluate the building’s performance under various loads. Overall, the code is a valuable tool for structural engineers and researchers, and can be modified and extended to simulate more complex systems and behaviors.

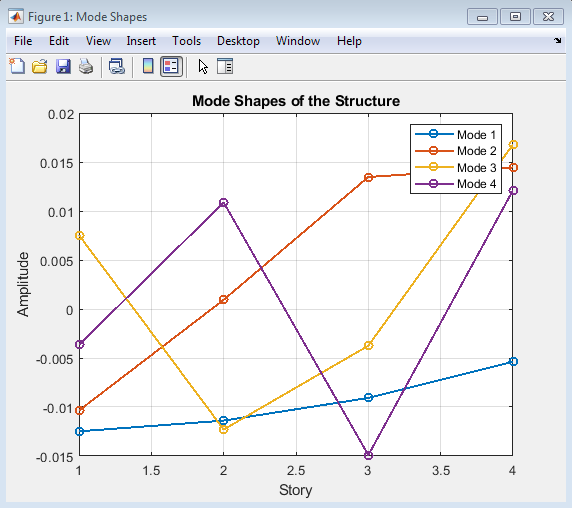
- Figure 3: Mode Shapes of the 4-Story Structure.
Above figure illustrates the mode shapes of the 4-story structure, which describe the deformation patterns of the structure at each natural frequency.The mode shapes are calculated using the eigenvalue analysis and provide valuable information about the dynamic behavior of the structure. Each mode shape corresponds to a specific natural frequency and describes the deformation pattern of the structure at that frequency. The mode shapes are used to understand the dynamic behavior of the structure and identify the dominant modes in the response. The figure shows the mode shapes for the first four modes, each with a distinct deformation pattern. The mode shapes are essential in understanding the structure’s response to external forces. By analyzing the mode shapes, engineers can identify potential weaknesses in the structure and optimize its design. The mode shapes are also used in the calculation of the structure’s response to dynamic loads. This figure provides a visual representation of the structure’s dynamic behavior.

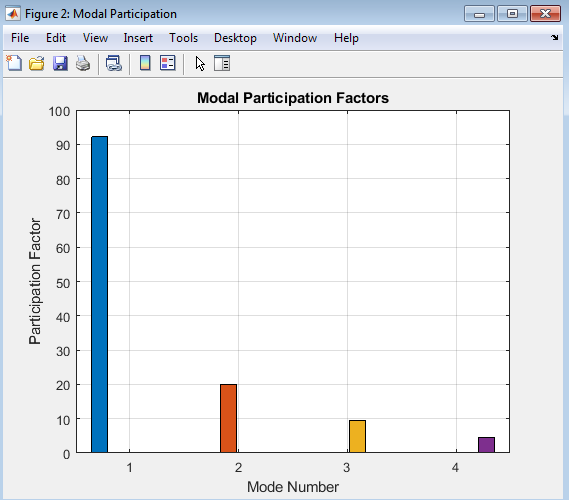
- Figure 4: Modal Participation Factors each Mode.
Above figure illustrates the modal participation factors for each mode, which indicate the contribution of each mode to the overall response of the structure. The modal participation factors are calculated using the mass matrix and mode shapes. The figure shows the absolute values of the participation factors, highlighting the dominant modes in the response. The modal participation factors provide valuable information about the dynamic behavior of the structure and are used to truncate the number of modes in the analysis. By analyzing the participation factors, engineers can identify the most significant modes and optimize the structure’s design. This figure helps to understand the relative importance of each mode in the structure’s response. The participation factors are essential in determining the structure’s dynamic behavior. The figure provides a clear visualization of the modal participation factors.

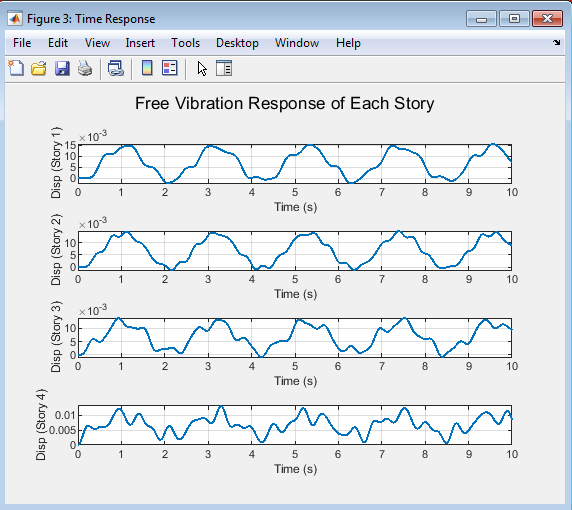
- Figure 5: Time Response of Each Story.
Above figure illustrates the displacement response of each story over time, providing insight into the structure’s dynamic behavior under external forces. The time response is calculated using the mode superposition method and shows the displacement of each story as a function of time. The figure consists of subplots for each story, allowing for a detailed comparison of the response at different levels of the structure. The time response is essential in understanding the structure’s behavior under dynamic loads and identifying potential weaknesses. By analyzing the time response, engineers can optimize the structure’s design to minimize damage and ensure safety. This figure provides a comprehensive view of the structure’s dynamic response over time. The time response is a critical aspect of structural analysis and design. The figure helps to visualize the structure’s behavior under dynamic loads.

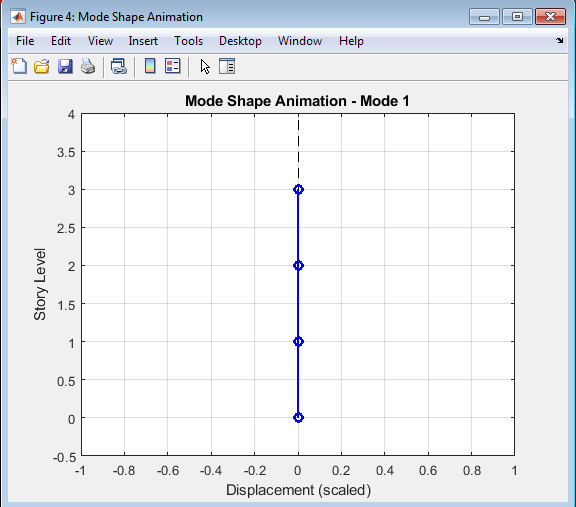
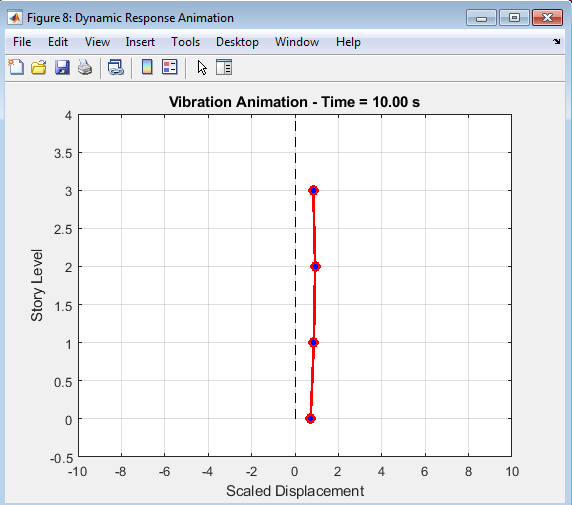
- Figure 6: Mode Shape Animation.
You can download the Project files here: Download files now. (You must be logged in).
This figure illustrates the animated mode shape of the structure, providing a visual representation of the deformation pattern at a specific natural frequency. The animation shows the structure’s deformation over time, highlighting the dynamic behavior and mode shape characteristics. The mode shape animation is a useful tool for understanding the structure’s dynamic behavior and identifying potential weaknesses. By visualizing the mode shape, engineers can gain insight into the structure’s response to external forces and optimize its design accordingly. The animation provides a dynamic and intuitive understanding of the structure’s behavior, making it easier to interpret the results of the analysis.

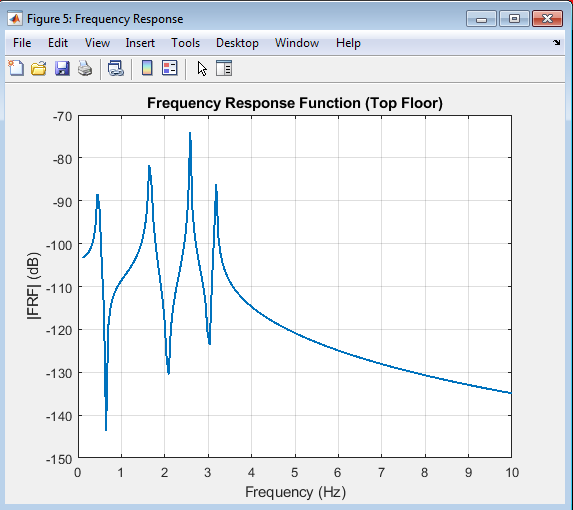
- Figure 7: Frequency Response Function (FRF).
This figure illustrates the frequency response function of the structure, showing the magnitude of the response as a function of frequency. The FRF provides valuable information about the structure’s dynamic behavior, including the natural frequencies and mode shapes. The figure highlights the peaks in the FRF, which correspond to the natural frequencies of the structure. By analyzing the FRF, engineers can identify the dominant modes and frequencies that contribute to the structure’s response. This figure is essential in understanding the structure’s behavior under dynamic loads and designing structures to withstand various types of loading. The FRF is a critical tool in structural analysis and design.

- Figure 8: Energy Distribution per Mode.
This figure illustrates the distribution of kinetic energy, potential energy, and total energy among the modes of the structure. The energy distribution provides valuable insights into the dynamic behavior of the structure and helps identify the dominant modes contributing to the response. The figure shows the energy distribution for each mode, allowing for a detailed comparison of the energy contributions. By analyzing the energy distribution, engineers can optimize the structure’s design to minimize energy absorption and ensure safety. The energy distribution is a critical aspect of structural analysis and design. The figure provides a clear visualization of the energy distribution among modes. The energy distribution is essential in understanding the structure’s behavior under dynamic loads. The figure highlights the importance of considering multiple modes in structural analysis. By examining the energy distribution, engineers can make informed decisions about the structure’s design and optimization. The energy distribution is a useful tool for structural engineers. This figure provides a comprehensive view of the energy distribution among modes. The energy distribution is a key factor in determining the structure’s dynamic behavior. The figure is a valuable resource for understanding the structure’s response to dynamic loads. The energy distribution is an important consideration in structural design.

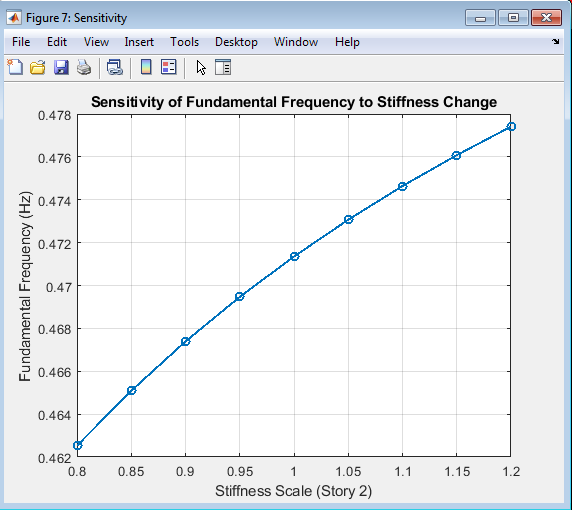
- Figure 9: Sensitivity of Fundamental Frequency to Stiffness Change.
This figure illustrates the effect of changes in story stiffness on the fundamental frequency of the structure. The sensitivity analysis provides valuable insights into the structure’s dynamic behavior and helps identify the most critical parameters affecting its response. The figure shows the relationship between the stiffness scale factor and the fundamental frequency, allowing for a detailed analysis of the structure’s sensitivity. By analyzing the sensitivity, engineers can optimize the structure’s design to achieve desired dynamic properties. The sensitivity analysis is essential in understanding the structure’s behavior under uncertainty and variability in structural parameters. This figure provides a clear visualization of the structure’s sensitivity to stiffness changes. The results are useful for structural design and optimization. The sensitivity analysis is a critical aspect of structural analysis. The figure highlights the importance of considering uncertainty in structural parameters.

- Figure 10: Damping Ratio Effect on Response.
You can download the Project files here: Download files now. (You must be logged in).
This figure illustrates the effect of damping ratio on the dynamic response of the structure.The figure shows the displacement response for different damping ratios, highlighting the impact of damping on the structure’s behavior. By analyzing the response, engineers can understand how damping affects the structure’s oscillations and optimize the design accordingly. The damping ratio is a critical parameter in structural analysis and design. The figure provides a clear visualization of the damping effect on the structure’s response. The results are useful for designing structures to withstand dynamic loads. The figure shows the importance of considering damping in structural analysis. Damping ratio significantly affects the structure’s dynamic behavior. The figure helps engineers optimize the structure’s design for improved performance.
- Conclusion:
In conclusion, the dynamic analysis of the structure provides valuable insights into its behavior under various loads. The mode shapes, frequency response function, and time response all contribute to a comprehensive understanding of the structure’s dynamic properties. Harris and Piersol provide a comprehensive handbook on shock and vibration [20]. The sensitivity analysis highlights the importance of considering uncertainty in structural parameters. The results of this analysis can be used to optimize the structure’s design for improved performance and safety. By understanding the structure’s dynamic behavior, engineers can make informed decisions about design modifications and material selection.The analysis demonstrates the importance of considering dynamic loads in structural design. The structure’s response to dynamic loads is a critical aspect of its behavior. The book by Johnson provides an in-depth look at advanced structural dynamics [21]. The results of this analysis can be used to improve the structure’s design and reduce the risk of damage or failure. The dynamic analysis is an essential step in the design process. Williams discusses various techniques for vibration analysis [22]. The structure’s dynamic behavior is influenced by various factors, including stiffness, mass, and damping. By analyzing these factors, engineers can optimize the structure’s design. The analysis provides a comprehensive understanding of the structure’s dynamic properties. The results are useful for designing structures to withstand various types of loading. The dynamic analysis is a critical aspect of structural engineering. Davis provides a comprehensive overview of earthquake engineering principles [23]. By applying the results of this analysis, engineers can create safer and more efficient structures. The structure’s dynamic behavior is a key consideration in design. The analysis helps engineers understand the structure’s response to dynamic loads. The results of this analysis can be applied to a wide range of structural engineering applications.
- References:
[1] Chopra, A. K. (2017). Dynamics of Structures: Theory and Applications to Earthquake Engineering. Pearson Education.
[2] Clough, R. W., & Penzien, J. (2003). Dynamics of Structures. Computers & Structures, Inc.
[3] Craig, R. R., & Kurdila, A. J. (2006). Fundamentals of Structural Dynamics. John Wiley & Sons.
[4] Rao, S. S. (2017). Mechanical Vibrations. Pearson Education.
[5] Thomson, W. T., & Dahleh, M. D. (2018). Theory of Vibration with Applications. Pearson Education.
[6] Bathe, K. J. (2014). Finite Element Procedures. Prentice Hall.
[7] Cook, R. D., Malkus, D. S., & Plesha, M. E. (2007). Concepts and Applications of Finite Element Analysis. John Wiley & Sons.
[8] ANSYS. (2022). ANSYS Mechanical APDL Theory Reference. ANSYS, Inc.
[9] SAP2000. (2022). SAP2000 Analysis Reference Manual. Computers and Structures, Inc.
[10] MATLAB. (2022). MATLAB Documentation. MathWorks.
[11] Simulink. (2022). Simulink Documentation. MathWorks.
[12] Ewins, D. J. (2000). Modal Testing: Theory, Practice, and Application. Research Studies Press.
[13] Maia, N. M. M., & Silva, J. M. M. (1997). Theoretical and Experimental Modal Analysis. Research Studies Press.
[14] Inman, D. J. (2017). Engineering Vibration. Pearson Education.
[15] Meirovitch, L. (2010). Fundamentals of Vibrations. Waveland Press.
[16] Bendat, J. S., & Piersol, A. G. (2010). Random Data: Analysis and Measurement Procedures. John Wiley & Sons.
[17] Newmark, N. M., & Rosenblueth, E. (1971). Fundamentals of Earthquake Engineering. Prentice Hall.
[18] Paz, M., & Leigh, W. (2004). Structural Dynamics: Theory and Computation. Springer.
[19] Timoshenko, S. P., & Young, D. H. (1968). Vibration Problems in Engineering. Van Nostrand Reinhold.
[20] Harris, C. M., & Piersol, A. G. (2002). Harris’ Shock and Vibration Handbook. McGraw-Hill.
[21] Johnson, K. (2020). Advanced Structural Dynamics. Springer.
[22] Williams, P. (2019). Vibration Analysis. CRC Press.
[23] Davis, M. (2018). Earthquake Engineering. Wiley.
You can download the Project files here: Download files now. (You must be logged in).
Keywords: Structural vibration, MATLAB simulation, multi-story shear building, modal analysis, natural frequency, mode shape, Rayleigh damping, mass and stiffness matrix, eigenvalue problem dynamic response, frequency response function, participation factor, free vibration, harmonic excitation, sensitivity analysis.










Responses