A Multi-Agent Reinforcement Learning-Based Data-Driven Method for Home Energy Management

Abstract

This paper proposes a novel framework for home energy management (HEM) based on reinforcement learning in achieving efficient home-based demand response (DR). The concerned hour-ahead energy consumption scheduling problem is duly formulated as a finite Markov decision process (FMDP) with discrete time steps. To tackle this problem, a data-driven method based on neural network (NN) and Q-learning algorithm is developed, which achieves superior performance on cost-effective schedules for HEM system. Specifically, real data of electricity price and solar photovoltaic (PV) generation are timely processed for uncertainty prediction by extreme learning machine (ELM) in the rolling time windows. The scheduling decisions of the household appliances and electric vehicles (EVs) can be subsequently obtained through the newly developed framework, of which the objective is dual, i.e., to minimize the electricity bill as well as the DR induced dissatisfaction. Simulations are performed on a residential house level with multiple home appliances, an EV and several PV panels. The test results demonstrate the effectiveness of the proposed data-driven based HEM framework.

1. INTRODUCTION

WITH recent advances in communication technologies and smart metering infrastructures, users can schedule their real-time energy consumption via the home energy management (HEM) system. Such actions of energy consumption scheduling are also referred to as demand response (DR), which balances supply and demand by adjusting elastic loads [1], [2]. Many research efforts have been paid on studying HEM system from the demand side perspective. In [3], a hierarchical energy management system is proposed for home microgrids with consideration of photovoltaic (PV) energy integration in day-ahead and real-time stages. Reference [4] studies a novel HEM system in finding optimal operation schedules of home energy resources, aiming to minimize daily electricity cost and monthly peak energy consumption penalty. Authors in [5] propose a stochastic programming based dynamic energy management framework for the smart home with plug-in electric vehicle storage. The work presented in [6] proposes a new smart HEM system in terms of the quality of experience, which depends on the information of consumer’s discontent for changing operations of home appliances. In [7], for the smart home equipped with heating, ventilation and air condition, Yu et al. investigate the issue of minimizing electricity bill and thermal discomfort cost simultaneously from the perspective of a long-term time horizon. Reference [8] proposes a multi-time and multi-energy building energy management system, which is modeled as a non-linear quadratic programming problem. Reference [9] utilizes an approximate dynamic programming method to develop a computationally efficient HEM system where temporal difference learning is adopted for scheduling distributed energy resources.

The study reported in [10] introduces a new approach for HEM system to solve a DR problem which is formulated using the chance-constrained programming optimization, combining the particle swarm optimization method and the two-point estimation method. Till now, most studies related to HEM system adopt centralized optimization approaches. Generally, due to the assumption of the accurate uncertainty prediction, the optimization method is able to show the perfect performance. However, this assumption is not very reasonable in reality since the optimization model knows all environment information meanwhile removing all prediction errors. Besides, due to a large number of binary or integer variables involved, some of these methods may suffer from expensive computational cost. As an emerging type of machine learning, reinforcement learning (RL) [11] shows excellent decision-making capability in the absence of initial environment information. The deployment of RL in decision-makings has considerable merits. Firstly, RL seeks the optimal actions by interacting with the environment so it has no requirement for initial knowledge, which may be difficult to acquire in practice. Secondly, RL can be flexibly employed to different application objects by off-line training and on-line implementation, considering relative uncertainties autonomously. Thirdly, RL is easier to implement in real-life scenarios as compared with conventional optimization methods. The reason is that RL can obtain the optimal results in a look-up table, so its computational efficiency is fairly high. In recent literature, the RL has received growing interests for solving energy management problems. Vázquez-Canteli and Nagy comprehensively summarizes the algorithms and modeling techniques for reinforcement learning for demand response. Interested readers can further refer to [12]. Reference [13] proposes a batch RL based approach for residential DR of thermostatically controlled loads with predicted exogenous data. In [14], Wan et al. use deep RL algorithms to determine the optimal solutions of the EV charging/discharging scheduling problem. In [15], RL is adopted to develop a dynamic pricing DR method based on hierarchical decision-making framework in the electricity market, which considers both profits of the service provider and costs of customers.

Reference [16] proposes an hour-ahead DR algorithm to make optimal decisions for different home appliances. Reference [17] proposes a residential energy management method considering peer-to-peer trading mechanism, where the model-free decision-making process is enhanced by the fuzzy Q-learning algorithm. In [18], a modelfree DR approach for industrial facilities is presented based on the actor-critic-based deep reinforcement learning algorithm. Based on RL, [19] proposes a multi-agent based distributed energy management method for distributed energy resources in a microgrid energy market. Reference [20] focuses on the deep RL based on-line optimization of schedules for the building energy management system. In [21], the deep neural network and the model-free reinforcement learning is utilized to manage the energy in a multi-microgrid system. Reference [22] presents a novel RL based model for residential load scheduling and load commitment with uncertain renewable sources. In consideration of the state-of-the-art HEM methods in this field, there are still two significant limitations. Firstly, most HEM studies focus only on one category of loads, such as home appliance loads or electric vehicle (EV) loads, ignoring the coordinated decision-makings for diverse loads. This weakly reflects the operational reality. Secondly, the integration of renewables, especially solar PV generation, is rarely considered during the decision-making process. With the rapid growth of rooftop installation of residential PV panels [23], allocation of self-generated solar energy should be considered when scheduling residential energy consumption. To address the above issues, this paper proposes a novel multi-agent reinforcement learning based data-driven HEM method. The hour-ahead home energy consumption scheduling problem is formulated as a finite Markov decision process (FMDP) with discrete time steps. The bi-objective of the formulated problem is to minimize the electricity bill as well as DR induced dissatisfaction cost. The main contributions of this paper are threefold.

1. Under the data-driven framework, we propose a novel model-free and adaptable HEM method based on extreme learning machine (ELM) and Q-learning algorithm. To our best knowledge, such method is rarely investigated before. The test results show that the proposed HEM method can not only achieve promising performance in terms of reducing electricity cost for householders but also improve the computational efficiency.
2. The conventional HEM methods are based on optimization algorithms with the assumption of perfect uncertainty prediction. However, this assumption is infeasible and unreasonable since the prediction errors are unavoidable. By contrast, our proposed model-free data-driven based HEM method can overcome the future uncertainties by the ELM based NN and discover the optimal DR decisions by the learning capability of the Q-learning algorithm.
3. In confronting with different types of loads in a residential house (e.g., non-shiftable loads, power-shiftable loads, time-shiftable loads and EV charging loads), a multi-agent Q-learning algorithm based RL method is developed to tackle the HEM problem involved with multiple loads. In this way, optimal energy consumption scheduling decisions for various home appliances and EV charging can be obtained in a fully decentralized manner. The remainder of this paper is organized as follows. Section II models the home energy consumption scheduling

Problem as a FMDP. Then our proposed solution approach is presented in Section III. In Section IV, test results are given to demonstrate the effectiveness of our proposed methodology. Finally, Section V concludes the paper.

2.  PROBLEM MODELLING

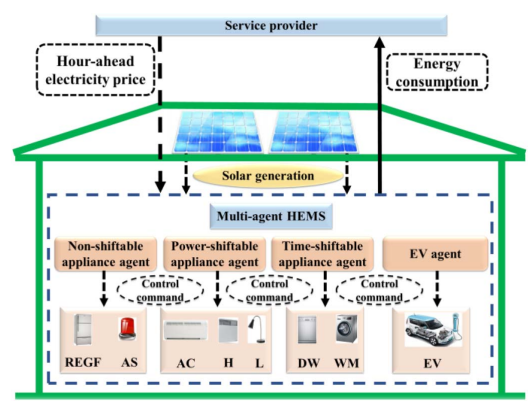
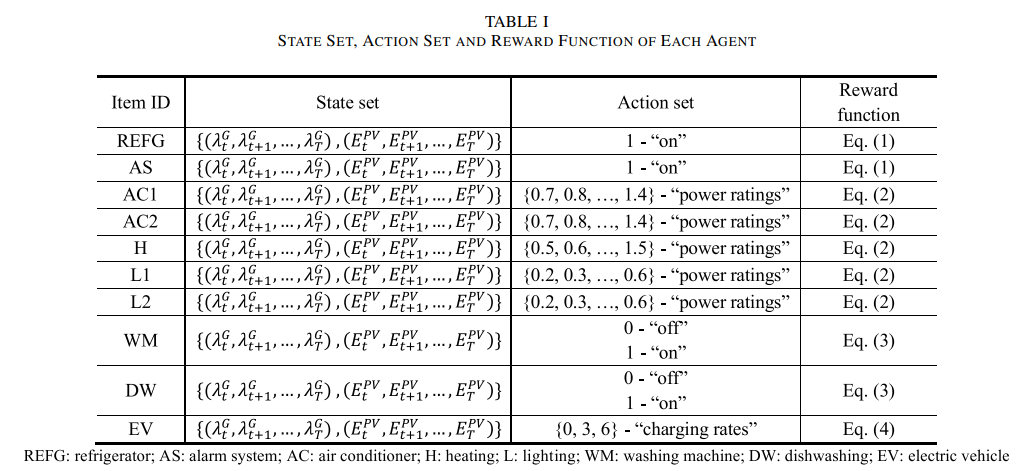
As illustrated in Figure. 1, this paper considers four agents in a HEM system, which correspond to non-shiftable appliance load, power-shiftable appliance load, time-shiftable appliance load, and EV load, respectively. In this paper, we envision the proposed HEM system includes multiple agents, which are virtual to control different kinds of smart home appliances in a decentralized manner. It should note that smart meters are assumed to be installed on smart home appliances to monitor the devices and receive the control command given by the agents. In each time slot, we determine the hour-ahead energy consumption actions for home appliances and EVs. Specifically, in time slot t, the agent observes the state st and chooses the action at. After taking this action, the agent observes the new state st+1 and chose a new action at+1 for the next time slot t + 1. This hour-ahead energy consumption scheduling problem can be formulated as a FMDP, where the outcomes are partly controlled by the decisionmaker and partly random. The FMDP of our problem contains five tuples, i.e., (S,A,R(·, ·), γ , θ ), where S denotes the state set, A denotes the finite action set, R(·, ·) denotes the reward set, γ denotes the discount rate and θ denotes the learning rate. The details about the FMDP formulation are described as follows.

• State

The state st can describe the current situation in the FMDP. In this paper, the state st in time slot t can be defined as a vector, defined as,

You can download the Project files here: Download files now. (You must be logged in).

• Action

In this study, the action denotes the energy consumption scheduling of each home appliance as well as EV battery charging, described as follows.

1) Action Set for Non-Shiftable Appliance Agent: Nonshiftable appliances, e.g., refrigerator and alarm system, require high reliability to ensure daily-life convenience and safety, so their demands must be satisfied and cannot be scheduled. Therefore, only one action, i.e., “on”, can be taken by the non-shiftable appliance agent.

2) Action Set for Power-Shiftable Appliance Agent: Powershiftable appliances, such as air conditioner, heating and light, can operate flexibly by consuming energy in a predefined range. Hence, power-shiftable agents can choose discrete actions, i.e., 1, 2, 3,…, which indicate the power ratings at different levels.

3) Action Set for Time-Shiftable Appliance Agent: The time-shiftable loads can be scheduled from peak periods to off-peak periods to reduce the electricity cost and avoid peak energy usage. Time-shiftable appliances, including wash machine and dishwasher, have two operating points, “on” and “off”. 4) Action Set for EV Agent: As the EV user, the householder would like to reduce electricity cost by scheduling EV battery charging. It should be noted that in this paper, EV battery discharging is not considered since it can significantly shorten the useful lifetime of EV battery [26]. As suggested by [27], the EV charger can provide discrete charging rates.

• Reward

The reward represents the inverse utility cost of each agent, described as follows.

The Reward of Non-Shiftable Appliance Agent:

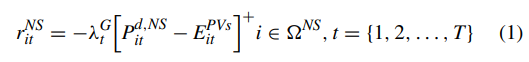
The reward of non-shiftable appliance agent only concerns on electricity cost since the non-shiftable loads are immutable. Note that [ · ] + represents the projection operator onto the nonnegative orthant, i.e., [x] + = max(x, 0).

3. PROPOSED DATA-DRIVEN BASED SOLUTION METHOD

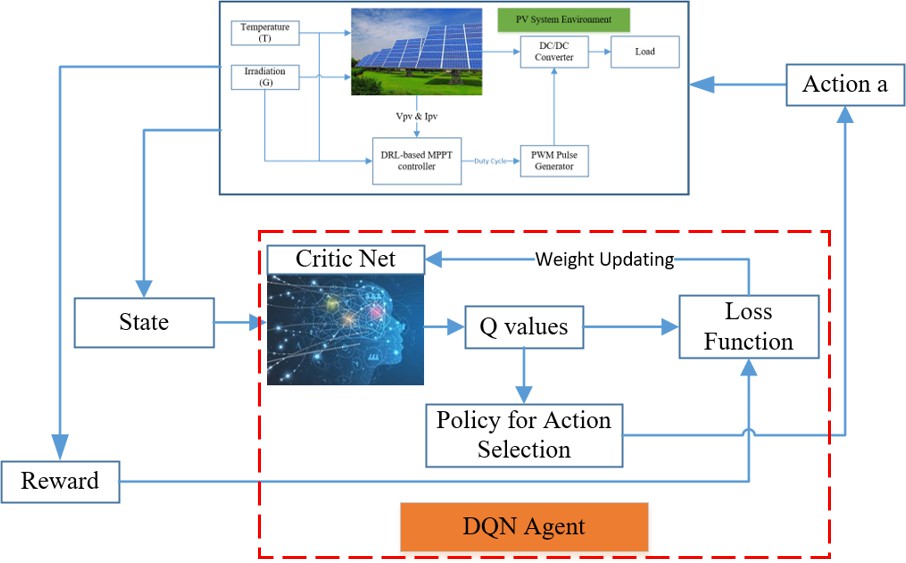
In this paper, the proposed reinforcement learning based data-driven method is comprised of two parts (see Fig. 2), (i) an ELM based feedforward NN is trained for predicting the future trends of electricity price and PV generation, (ii) a multi-agent Q-learning algorithm based RL method is developed for making hour-ahead energy consumption decisions. Details of this data-driven based solution method are given in the following subsections.

• ELM Based Feedforward NN for Uncertainty Prediction

As a well-studied training algorithm, ELM algorithm has become a popular topic in the fields of load forecasting [29], electricity price forecasting [30] and renewable generation forecasting [31]. Since the input weights and biases of the hidden layer are randomly assigned and free to be tuned further when using ELM algorithm, some exceptional features can be obtained, e.g., fast learning speed and good generalization. To deal with the uncertainties of electricity prices and solar generations, we propose an ELM based feedforward NN to dynamically predict future trends of these two uncertainties. Specifically, at each hour, the inputs of the trained feedforward NN are past 24-hour electricity price data and solar generation data, and its outputs are the forecasted future 24-hour trends of electricity prices and solar generations. This predicted information will be fed into the decision-making process of energy consumption scheduling, as described in the following subsection.

• Multi-Agent Q-Learning Algorithm for Decision-Making

After acquiring the predicted future electricity prices and solar panel outputs, we employ the Q-learning algorithm to use this information to find the optimal policy π∗. As an emerging machine learning algorithm, Q-learning algorithm is widely used for the decision-making process to gain the maximum cumulative rewards [32]. The basic mechanism of

This algorithm is to construct a Q-table where Q-value Q(st, at) of each state-action pair is updated in each iteration until the convergence condition is satisfied. In this way, the optimal action with optimal Q-value in each state can be selected. The optimal Q-value Q∗ π (st, at) can be obtained by using Bellman equation [33], given as below,

The Q-value can be updated in terms of reward, learning rate and discount factor, described as follows,

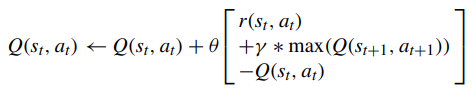
where θ ∈ [0, 1] denotes the learning rate indicating to what extent the new Q-value can overturn the old one. When θ = 0, the agent exploits the prior information exclusively, whereas θ = 1 indicates that the agent considers only the current estimate and overlooks the prior information. A value of a decimal between 0 and 1 should be applied to θ, trading off the new Q-value and old Q-value.

• Implementation Process of Proposed Solution Method

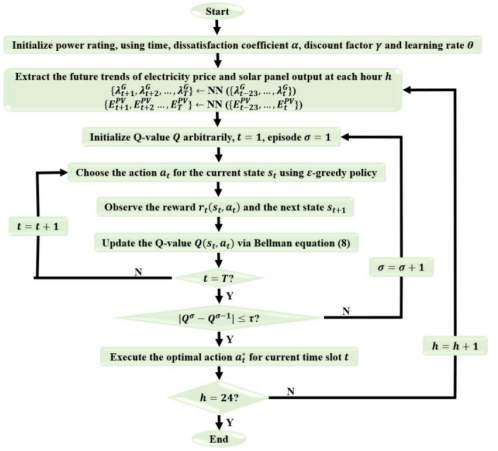
Algorithm  1 demonstrates the implementation process of our proposed solution approach for solving the FMDP problem as described in Section II. Specifically, in the initial time slot, i.e., t = 1, the HEM system initializes power rating, dissatisfaction coefficient, discount rate, and learning rate. In each time slot,the trained DFM is used to forecast future 24-hour electricity prices as well as solar panel outputs, as shown in Algorithm 2. Upon obtaining the predicted information, the multi-agent Q-learning algorithm is adopted to make ideal energy scheduling decisions for different residential

Appliances and EV battery charging iteratively, as shown in Algorithm 3. Specifically, in each episode σ, the agent observes the state st and then chooses an action at using the exploration and exploitation mechanism. To realize the exploration and exploitation, the ε-greedy policy (ε
[0, 1]) [34] is adopted so the agent can either execute a random action form the set of available actions with probability ε or select an action whose current Q-value is maximum, with probability 1−ε. After taking an action, the agent acquires an immediate reward r(st, at), observes the next state st+1 and updates the Q-value Q(st, at) via Eq. (8). This process is repeated until the state st+1 is terminal. After one episode, the agent checks the episode termination criterion, i.e., |Qσ −Qσ−1| ≤ τ , where τ is a system-dependent parameter to control the accuracy of the convergence. If this termination criterion is not satisfied, the agent will move to the next episode and repeat the above process. Finally, each agent will gain optimal actions for each coming hour, i.e., h = 1, 2,… 24. Note that only the optimal action for the current hour is taken. The above procedure will be repeated until the end hour, namely, h = 24. Besides, the flowchart in Fig. 3 clearly depicts the process.

You can download the Project files here: Download files now. (You must be logged in).

4.  TEST RESULTS

• Case Study Setup

In this study, real-world data is utilized for training our proposed feedforward NN. The hourly data electricity prices and solar generations from January 1, 2017 to December 31, 2018 lasting 730 days are collected from PJM [35]. After a number of accuracy tests, the trained feedforward NN for electricity price data consists of three layers, i.e., one input

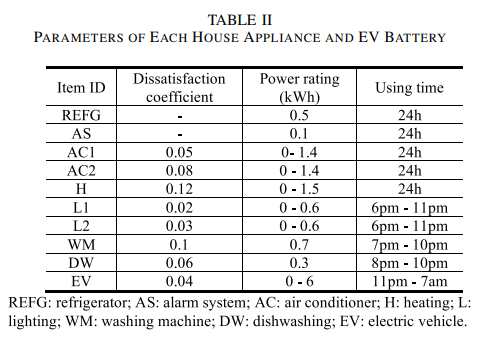
layer with 24 neurons, one hidden layer with 40 neurons and one output layer with 24 neurons, and the trained feedforward NN for solar generation data also includes three layers, i.e., one input layer with 24 neurons, one hidden layer with 20 neurons and one output layer with 24 neurons. The number of training episode is 50,000. As for the parameters related to the Q-learning algorithm. The discount rate γ is set to 0.9, so the obtained strategy is foresighted. To ensure that the agent can call all state-action pairs and learn new knowledge from the system, the learning rate θ as well as turning parameter ε are both set to 0.1. In this paper, simulations are conducted on a detached residential house with two same solar panels, two non-shiftable appliances (REFG and AS), five power-shiftable appliances (AC1, AC2, H, L1 and L2), two time-shiftable appliances (WM and DW) and one EV. Detailed parameters of these home appliances and the EV battery are listed in Table II. Besides, our proposed HEM method can be applied to residential houses with more home appliances and renewable resources.

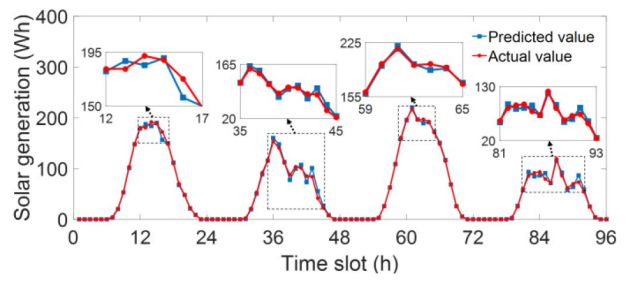
All simulations are implemented by using MATLAB with an Intel Core i7 of 2.4 GHz and 12GB memory.

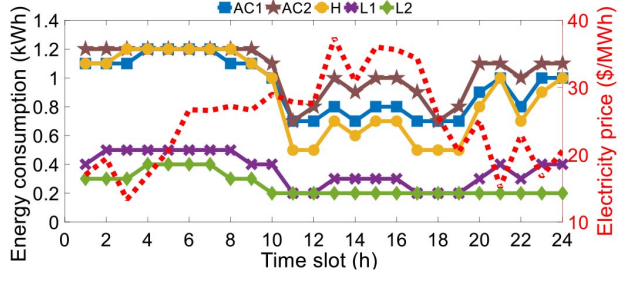
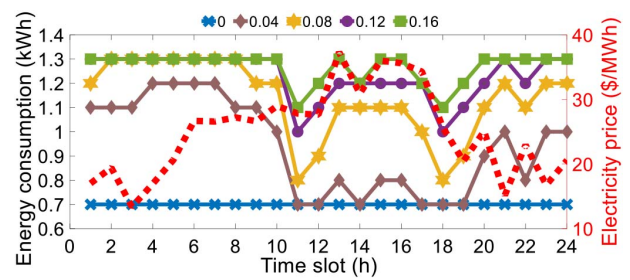
Figure 7 demonstrates the results of daily energy consumption for AC1 with different five dissatisfaction coefficients. We can see that as the dissatisfaction coefficient increases, the daily energy consumption goes up since the dissatisfaction coefficient can be regarded as a penalty factor. This creates a trade-off between saving electricity bill and decreasing dissatisfaction caused by reducing power rating of AC1. Besides, this figure also shows that the agent leans to increase energy consumption for low dissatisfaction during the off-peak time slots and decrease energy consumption for low electricity cost during the on-peak time slots. These observations verify that the proposed method can be applied to consumers for helping them manage their individual energy consumption.

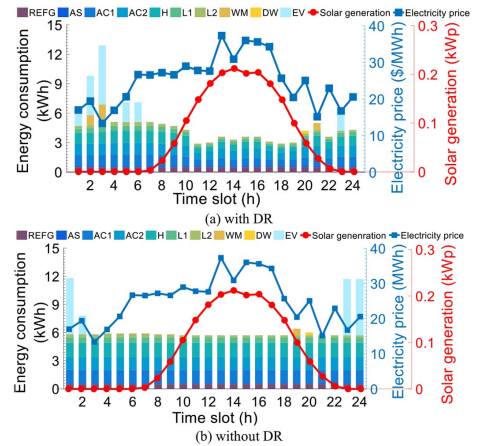
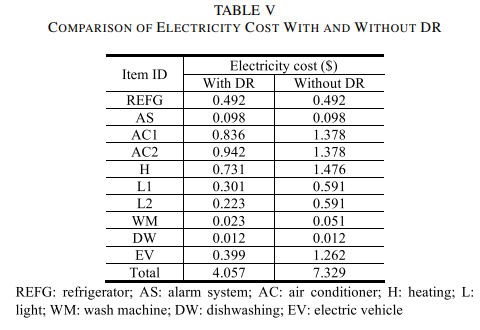
Figure 8 gives the daily energy consumption of each home appliance and EV in two different cases with and without DR, along with the electricity prices and solar panel outputs. With DR mechanism, more energy is consumed when the price is low, and the load demand is reduced when the price is high, as shown in Figure 8 (a). Thus, the power-shiftable or time-shiftable loads can be reduced or scheduled to off-peak periods, maintaining the overall energy consumption at a low level during the on-peak periods. By contrast, for the case without DR, as shown in Figure 8 (b), no reduction or shift on energy consumption can be observed. The comparison of electricity costs in these two cases is listed in Table V, which shows that the electricity cost can be significantly reduced with DR.

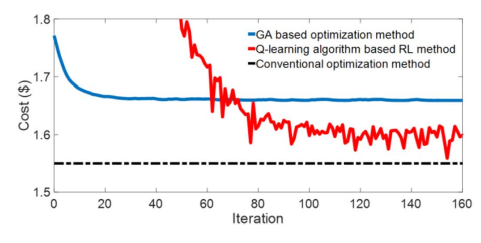
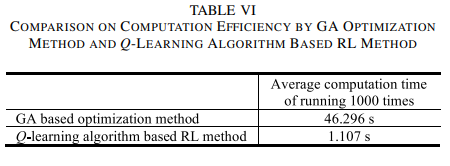
method adapts to the learning environment and adjusts its policy via exploration and exploitation mechanism. For a longer time, it outperforms the GA based solution method (blue line). The reason is that the RL agent not only considers the current reward but also the future rewards so it can learn from the environment while the GA algorithm has low learning capability. Note that the black dashed line in Fig. 11 is plotted as the benchmark to show the optimal result obtained by the conventional optimization method, which knows all environment information and removes prediction errors. Besides, Table VI is added to compare the computation efficiency between the proposed solution method and benchmark. It can be observed that our proposed solution method is able to significantly reduce the computation time. The reasons can be summarized into two aspects: 1) GA algorithm is based on Darwin’s theory of evolution, which is a slow gradual process that works by making changes to the making slight and slow changes. Moreover, GA usually makes slight changes to its solutions slowly until getting the best solution. 2) In the Q-learning algorithm, the agent chooses an action using the exploration and exploitation mechanism, so it is fast by employing the ε-greedy policy to explore and exploit the optimum from the look-up table. Note that only a small number of state-action pairs need to be searched by the Q-learning algorithm, resulting in a high computation efficiency. In this regard, considering the adaptivity of model-free RL to the external environment, our proposed Q-learning based solution method is suggested to solve HEM problems.

You can download the Project files here: Download files now. (You must be logged in).

4. CONCLUSION

Based on a feedforward NN and Q-learning algorithm, this paper proposes a new multi-agent RL based data-driven method for HEM system. Specifically, ELM is employed to train the feedforward NN to predict future trends of electricity price and solar generation according to real-world data. Then, the predicted information is fed into the multiagent Q-learning algorithm based decision-making process for scheduling the energy consumption of different home appliances and EV charging. To implement the proposed HEM method, the FMDP is utilized to model the hour-ahead energy consumption scheduling problem with the objective of minimizing the electricity bill as well as DR included dissatisfaction. Simulations are performed on a residential house with multiple home appliances, an EV and several PV panels. The test results show that the proposed HEM method can not only achieve promising performance in terms of reducing electricity cost for householders but also improve the computational efficiency. In the future, energy storage for rooftop solar PV systems will also be considered in the HEM system. Besides, more effective uncertainty prediction model will be developed to facilitate the decision-making process of DR.

REFERENCES

1. Shareef, M. S. Ahmed, A. Mohamed, and E. Al Hassan, “Review on home energy management system considering demand responses, smart technologies, and intelligent controllers,” IEEE Access, vol. 6, pp. 24498–24509, 2018.
2. Chen, Y. Xu, Z. Li, and X. Feng, “Optimally coordinated dis- patch of combined-heat-and-electrical network with demand response,” IET Gener. Transm. Distrib., vol. 13, no. 11, pp. 2216–2225, Jun. 2019.
3. Luo, G. Ranzi, S. Wang, and Z. Y. Dong, “Hierarchical energy man- agement system for home microgrids,” IEEE Trans. Smart Grid, vol. 10, no. 5, pp. 5536–5546, Sep. 2019.
4. Luo, W. Kong, G. Ranzi, and Z. Y. Dong, “Optimal home energy management system with demand charge tariff and appliance opera- tional dependencies,” IEEE Trans. Smart Grid, vol. 11, no. 1, pp. 4–14, Jan. 2020.
5. Wu, X. Hu, X. Yin, and S. J. Moura, “Stochastic optimal energy management of smart home with PEV energy storage,” IEEE Trans. Smart Grid, vol. 9, no. 3, pp. 2065–2075, May 2018.
6. Pilloni, A. Floris, A. Meloni, and L. Atzori, “Smart home energy management including renewable sources: A QoE-driven approach,” IEEE Trans. Smart Grid, vol. 9, no. 3, pp. 2006–2018, May 2016.
7. Yu, T. Jiang, and Y. Zou, “Online energy management for a sustain- able smart home with an HVAC load and random occupancy,” IEEE Trans. Smart Grid, vol. 10, no. 2, pp. 1646–1659, Mar. 2019.
8. Sharma, Y. Xu, A. Verma, and B. K. Panigrahi, “Time- coordinated multi-energy management of smart buildings under uncer- tainties,” IEEE Trans. Ind. Informat., vol. 15, no. 8, pp. 4788–4798, Aug. 2019.
9. Keerthisinghe, G. Verbiè, and A. C. Chapman, “A fast technique for smart home management: ADP with temporal difference learning,” IEEE Trans. Smart Grid, vol. 9, no. 4, pp. 3291–3303, Jul. 2018.
10. Huang, L. Wang, W. Guo, Q. Kang, and Q. Wu, “Chance constrained optimization in a home energy management system,” IEEE Trans. Smart Grid, vol. 9, no. 1, pp. 252–260, Jan. 2018.
11. S. Sutton and A. G. Barto, Introduction to Reinforcement Learning. Cambridge, MA, USA: MIT Press, 1998.
12. R. Vázquez-Canteli and Z. Nagy, “Reinforcement learning for demand response: A review of algorithms and modeling techniques,” Appl. Energy, vol. 235, pp. 1072–1089, Feb. 2019.
13. Ruelens, B. J. Claessens, S. Vandael, B. De Schutter, R. Babuška, and R. Belmans, “Residential demand response of thermostatically con- trolled loads using batch reinforcement learning,” IEEE Trans. Smart Grid, vol. 8, no. 5, pp. 2149–2159, Sep. 2017.
14. Wan, H. Li, H. He, and D. Prokhorov, “Model-free real-time EV charging scheduling based on deep reinforcement learning,” IEEE Trans. Smart Grid, vol. 10, no. 5, pp. 5246–5257, Sep. 2019.
15. Lu, S. H. Hong, and X. Zhang, “A dynamic pricing demand response algorithm for smart grid: Reinforcement learning approach,” Appl. Energy, vol. 220, pp. 220–230, Jun. 2018.
16. Lu, S. H. Hong, and M. Yu, “Demand response for home energy management using reinforcement learning and artificial neural network,” IEEE Trans. Smart Grid, vol. 10, no. 6, pp. 6629–6639, Nov. 2019.
17. Zhou, Z. Hu, W. Gu, M. Jiang, and X.-P. Zhang, “Artificial intel- ligence based smart energy community management: A reinforcement learning approach,” CSEE J. Power Energy Syst., vol. 5, no. 1, pp. 1–10, 2019.
18. Huang, S. H. Hong, M. Yu, Y. Ding, and J. Jiang, “Demand response management for industrial facilities: A deep reinforcement learning approach,” IEEE Access, vol. 7, pp. 82194–82205, 2019.
19. Foruzan, L.-K. Soh, and S. Asgarpoor, “Reinforcement learning approach for optimal distributed energy management in a microgrid,” IEEE Trans. Power Syst., vol. 33, no. 5, pp. 5749–5758, Sep. 2018.
20. Mocanu et al., “On-line building energy optimization using deep reinforcement learning,” IEEE Trans. Smart Grid, vol. 10, no. 4, 3698–3708, Jul. 2019.
21. Du and F. Li, “Intelligent multi-microgrid energy management based on deep neural network and model-free reinforcement learning,” IEEE Trans. Smart Grid, early access, doi: 10.1109/TSG.2019.2930299.
22. Remani, E. A. Jasmin, and T. P. I. Ahamed, “Residential load scheduling with renewable generation in the smart grid: A reinforce- ment learning approach,” IEEE Syst. J., vol. 13, no. 3, pp. 3283–3294, Sep. 2019.
23. McCabe, D. Pojani, and A. B. van Groenou, “Social housing and renewable energy: Community energy in a supporting role,” Energy Res. Soc. Sci., vol. 38, pp. 110–113, Apr. 2018.
24. A. Green, Solar Cells: Operating Principles, Technology, and System Applications. Englewood Cliffs, NJ, USA: Prentice-Hall, 1982.
25. Walker, “Evaluating MPPT converter topologies using a MATLAB PV model,” J. Elect. Electron. Eng., vol. 21, no. 1, p. 49, 2001.
26. M. Rezvanizaniani, Z. Liu, Y. Chen, and J. Lee, “Review and recent advances in battery health monitoring and prognostics technologies for electric vehicle (EV) safety and mobility,” J. Power Sources, vol. 256, 110–124, Jun. 2014.
27. Le Floch, E. C. Kara, and S. Moura, “PDE modeling and control of electric vehicle fleets for ancillary services: A discrete charging case,” IEEE Trans. Smart Grid, vol. 9, no. 2, pp. 573–581, Mar. 2018.
28. Yu and S. H. Hong, “Incentive-based demand response considering hierarchical electricity market: A Stackelberg game approach,” Appl. Energy, vol. 203, pp. 267–279, Oct. 2017.
29. Rafiei, T. Niknam, J. Aghaei, M. Shafie-Khah, and J. P. Catalão, “Probabilistic load forecasting using an improved wavelet neural network trained by generalized extreme learning machine,” IEEE Trans. Smart Grid, vol. 9, no. 6, pp. 6961–6971, Nov. 2018.
30. Chai, Z. Xu, and Y. Jia, “Conditional density forecast of electricity price based on ensemble ELM and logistic EMOS,” IEEE Trans. Smart Grid, vol. 10, no. 3, pp. 3031–3043, May 2019.
31. Fu, K. Wang, C. Li, and J. Tan, “Multi-step short-term wind speed forecasting approach based on multi-scale dominant ingredient chaotic analysis, improved hybrid GWO-SCA optimization and ELM,” Energy Convers. Manag., vol. 187, pp. 356–377, May 2019.
32. J. Watkins and P. Dayan, “Q-learning,” Mach. Learn., vol. 8, nos. 3–4, 279–292, 1992.
33. J. Kappen, “Optimal control theory and the linear Bellman equation,” in Inference Learning Dynamic Models, 2011, pp. 363–387. [Online]. Available: http://hdl.handle.net/2066/94184
34. Tokic and G. Palm, “Value-difference based exploration: Adaptive control between epsilon-greedy and softmax,” in Proc. Annu. Conf. Artif. Intell., 2011, pp. 335–346.
35. Attar, O. Homaee, H. Falaghi, and P. Siano, “A novel strategy for optimal placement of locally controlled voltage regulators in tra- ditional distribution systems,” Int. J. Elect. Power Energy Syst., vol. 96, 11–22, Mar. 2018.
36. R. Koza, Genetic Programming II, vol. 17. Cambridge, MA, USA: MIT Press, 1994.

You can download the Project files here: Download files now. (You must be logged in).

Keywords: Multi-Agent, Reinforcement Learning, Data-Driven, Home Energy Management, MATLAB, finite Markov decision process (FMDP), neural network (NN), Q-learning algorithm, solar photovoltaic (PV)

Do you need help with Energy management and MATLAB? Don’t hesitate to contact our Tutors to receive professional and reliable guidance.