A Multiphysics Computational Framework for Particle Manipulation in Microfluidic Channels: Integrating Dielectrophoretic, Acoustic, and Hydrodynamic Forces
Author: Waqas Javaid
Abstract
The field of microfluidics has revolutionized chemical and biological analysis by enabling the precise manipulation of particles and fluids at the microscale. Key to this capability is the application of force fields, such as electric, acoustic, and hydrodynamic, to separate, trap, and concentrate target particles like cells, bacteria, and exosomes. This project presents a comprehensive multiphysics computational model developed in MATLAB to simulate the complex interplay of these forces within a microfluidic channel. The framework consists of two primary modules: first, a 3D Finite Difference Method (FDM) solver for calculating electric potential and field distributions generated by a patterned electrode array, subsequently used to compute dielectrophoretic (DEP), buoyancy, gravitational, and inertial forces; and second, a dynamic displacement model that simulates particle trajectories under the influence of acoustic radiation and drag forces. The results demonstrate the model’s capability to predict particle behavior based on size and initial position, providing a powerful in-silico tool for the design and optimization of next-generation microfluidic devices for lab-on-a-chip applications.
Keywords: Microfluidics, Dielectrophoresis, Acoustic Radiation Force, Finite Difference Method, Gauss-Seidel, Particle Separation, MATLAB, Multiphysics Modeling.
- Introduction
Microfluidic technology, often referred to as “Lab-on-a-Chip” (LOC), aims to miniaturize and integrate entire biological or chemical laboratories onto a single chip-sized device [1]. The advantages of such systems are manifold: reduced consumption of samples and reagents, faster analysis times, high sensitivity, and potential for massive parallelization and portability [2]. A critical function in many microfluidic applications is the manipulation of suspended particles, which is essential for tasks such as cell sorting, pathogen detection, and exosome isolation [3].
The manipulation of particles at the microscale is governed by a different set of physical principles than those at the macroscale. Inertial forces become negligible, while surface forces, such as viscous drag and forces generated by external fields, dominate [4]. Two of the most prominent and versatile techniques for particle manipulation are Dielectrophoresis (DEP) and Acoustic Standing Wave (ASW) separation.
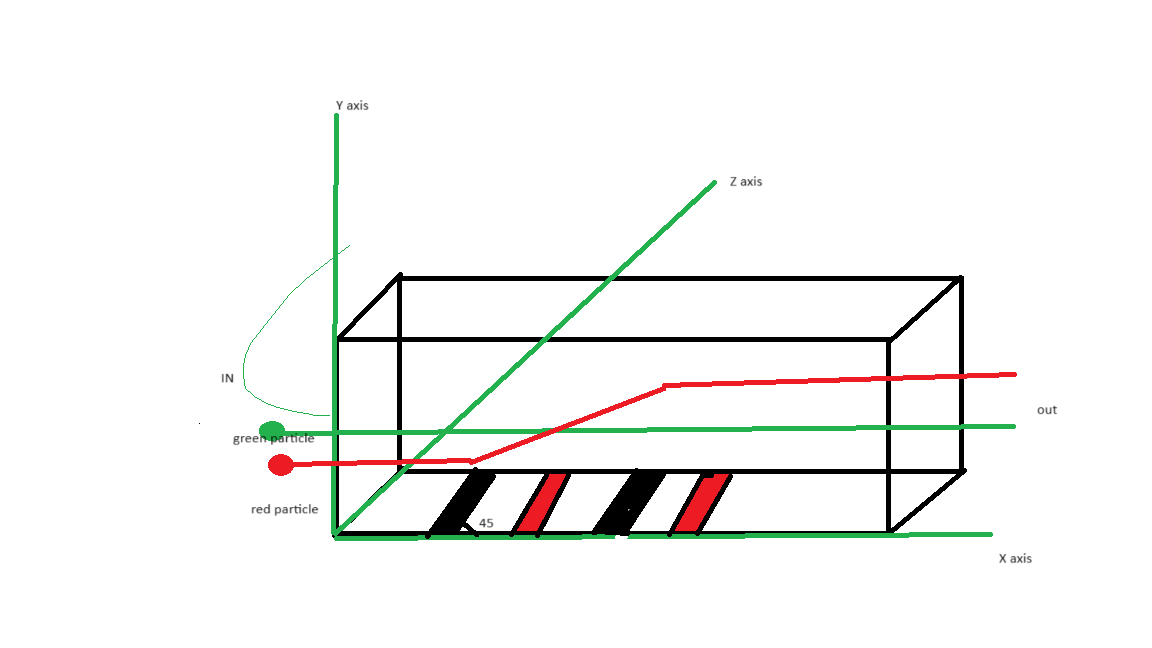

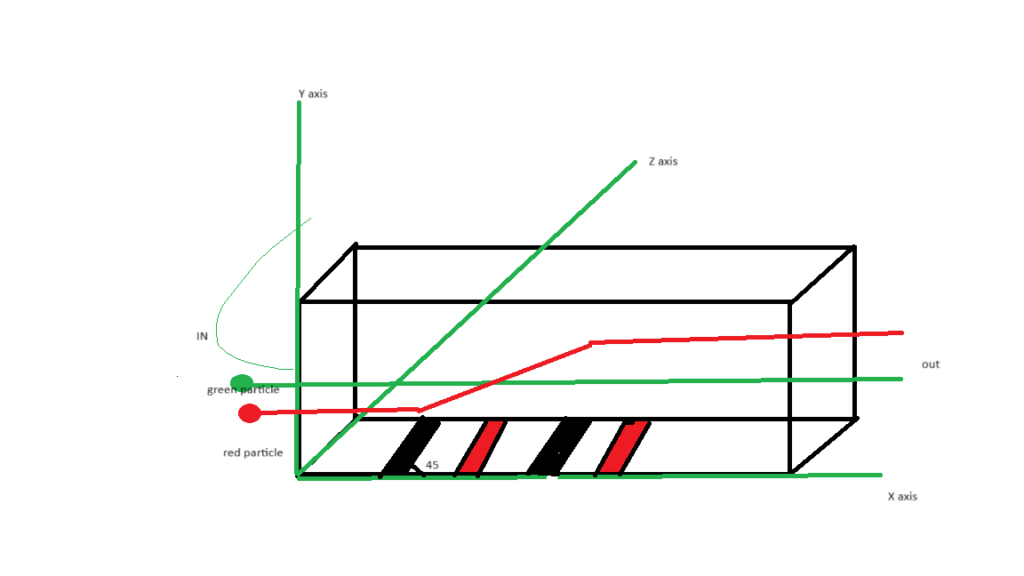
- Figure 1: Dielectrophoresis (DEP) and Acoustic Standing Wave (ASW)
Dielectrophoresis exploits the polarization differences between a particle and its suspending medium in a non-uniform electric field to exert a force on the particle [5]. Acoustic methods, particularly using standing surface acoustic waves (SSAW), utilize the momentum transfer from sound waves to particles, pushing them toward specific locations in the channel, such as pressure nodes or antinodes [6]. Often, these techniques are combined with the inherent hydrodynamic forces of the fluid flow to achieve enhanced separation resolution and throughput [7].
While experimental prototyping is crucial, it can be time-consuming and expensive. Computational modeling provides a powerful alternative for predicting device performance, optimizing design parameters, and gaining fundamental insights into the underlying physics before fabrication [8]. This report details the development and implementation of a sophisticated multiphysics model in MATLAB that simulates the 3D environment of a microfluidic channel and predicts particle trajectories under the combined influence of DEP, acoustic, hydrodynamic, buoyancy, and gravitational forces.
The project is structured in two synergistic parts:
- The Static 3D Force Field Solver: This module computes the electric potential from a complex electrode geometry, solves the Laplace equation using a numerical method, and derives the resultant force fields (DEP, buoyancy, gravity, inertia) throughout the entire channel volume.
- The Dynamic Particle Trajectory Simulator: This module focuses on the time-dependent motion of particles of varying sizes, primarily under acoustic radiation forces and fluid drag, providing trajectory data and displacement analysis.
- Theoretical Background
A robust understanding of the governing physical principles is essential to interpreting the model’s implementation and results.
2.1 Dielectrophoresis (DEP)
Dielectrophoresis is the motion of a polarizable particle in a non-uniform electric field. The time-average DEP force acting on a spherical particle is given by [5]:
![]()
where:
ϵm is the permittivity of the suspending medium.
r is the radius of the particle.
Erms is the root-mean-square magnitude of the electric field.
Re[fCM] is the real part of the Clausius-Mossotti (CM) factor, which depends on the complex permittivities of the particle and the medium.
The CM factor dictates the direction of the force. If Re[fCM]>0 (positive DEP), the particle is attracted to regions of high electric field gradient, typically near electrode edges. If Re[fCM]<0 (negative DEP), the particle is repelled from these regions toward areas of lower field strength [9]. In our model, the force calculation is implemented in a generalized vector form derived from this fundamental equation, as seen in the code:
matlab
F_DEP = (epsilon_p – epsilon_f) * V_p * E_squared * [Ex(j, i, k), Ey(j, i, k), Ez(j, i, k)] / (2 * epsilon_f);
2.2 Acoustic Radiation Force
When a standing acoustic wave is established in a microfluidic channel, particles experience a primary acoustic radiation force (ARF). For a standing wave perpendicular to the flow direction, this force pushes particles toward either the pressure nodes or antinodes of the wave. For a small, spherical particle in a standing plane wave, the ARF can be approximated by [6]:
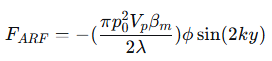
where:
p0 is the acoustic pressure amplitude.
Vp is the particle volume.
βm is the compressibility of the medium.
λ is the wavelength.
k=2π/λ is the wave number.
y is the position in the direction of the wave.
ϕ is the acoustic contrast factor, given by
![]()
The contrast factor, ϕ, determines the direction of the force. If ϕ>0, particles move to the pressure nodes (typically the channel centerline); if ϕ<0, they move to the antinodes (near the channel walls) [10]. Our model implements a discretized version of this force to calculate the "delta force" displacement in the y-direction.
2.3 Hydrodynamic and Body Forces
Particles in a microfluidic channel are also subject to other forces:
- Drag Force: Described by Stokes’ law for small Reynolds numbers, Fdrag=6πηru, where η is the dynamic viscosity and u is the relative velocity between the particle and the fluid [4].
- Buoyancy and Gravity: The net vertical force is Fbg=(ρp−ρf)Vpg. In our model, these are treated as separate components for detailed analysis.
- Inertial Force: In the context of the dynamic model, this refers to the force required to change the momentum of the particle and is related to the fluid’s flow velocity profile.
You can download the Project files here: Download files now. (You must be logged in).
- Methodology and Model Implementation
The computational framework was built entirely in MATLAB R2023a. The following sections detail the implementation of the two main modules.
3.1 Part 1: 3D Electric Field and Static Force Calculation
3.1.1 Geometry and Grid Definition
The model defines a rectangular channel with dimensions 160 m (length, x) × 40 m (width, y) × 50 m (depth, z). A structured Cartesian grid is created with a user-defined spacing of dNx = dNy = dNz = 5 m. This results in a grid of size (Ny, Nx, Nz) = (9, 33, 11) points. While this grid is relatively coarse, it was chosen for computational efficiency in this proof-of-concept model. A finer grid would provide higher accuracy at the cost of increased computation time [11].
Matlab
Nx = floor(rect_width / dNx) + 1;
Ny = floor(rect_height / dNy) + 1;
Nz = floor(channel_depth / dNz) + 1;[X, Y, Z] = meshgrid(0:dNx:rect_width, 0:dNy:rect_height, 0:dNz:channel_depth);
3.1.2 Electrode Design and Potential Initialization
A key feature is the implementation of a series of six parallelogram-shaped electrodes along the bottom of the channel (z=0). These are designed to create a strong, spatially periodic non-uniform electric field essential for DEP. The electrodes are patterned with alternating potentials of +10 V and -10 V.
Matlab
line_points(1,:) = [initial_gap, 0, initial_gap + par_height, par_height]; % +10 V
line_points(2,:) = [initial_gap + gap_between_lines + par_width, 0, … ]; % -10V…
A tolerance-based algorithm is used to identify grid points that lie “on” these electrode lines and assign them the fixed boundary potential (Vo or -Vo). This approach effectively discretizes the continuous electrode geometry onto the finite difference grid.
3.1.3 Numerical Solution of Laplace’s Equation
In the regions of the channel not occupied by electrodes, the electric potential, ΦΦ, is governed by Laplace’s equation: ∇2Φ=0 [12]. We employ the Finite Difference Method (FDM) to solve this equation numerically. The 3D Laplace equation is discretized using a central difference scheme, leading to the following approximation at any interior grid point (i,j,k)(i,j,k):
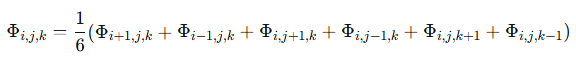
The Gauss-Seidel iterative method is used to solve this system of linear equations. This method is chosen for its simplicity and relatively low memory footprint, as it uses updated values as soon as they are available [13]. The iteration continues until the maximum error between successive solutions falls below a strict tolerance of 1×10−14.
Matlab
while Er >= tolerance_GS
kk = kk + 1;
Phi_old = Phi;
for i = 2:Nx-1
for j = 2:Ny-1
for k = 2:Nz-1
if Phi(j, i, k) ~= Vo && Phi(j, i, k) ~= -Vo
Phi(j, i, k) = (1/6) * (Phi(j+1, i, k) + … );
end
end
end
end
Er = max(max(max(abs(Phi – Phi_old))));end
3.1.4 Electric Field and Force Computation
Once the potential distribution Φ is known, the electric field E⃗is computed as its negative gradient: E⃗=−∇Φ. MATLAB’s gradient function is used for this purpose, providing the components Ex,Ey,Ez at every grid point.
Matlab
[Ex, Ey, Ez] = gradient(-Phi, dNx, dNy, dNz);
The forces are then calculated at every point in the grid:
- DEP Force: As previously described, using the calculated E⃗field.
- Buoyancy & Gravity: Explicitly calculated and applied in the z-direction.
- Inertial Force: A simplified force in the x-direction, proportional to the fluid velocity.
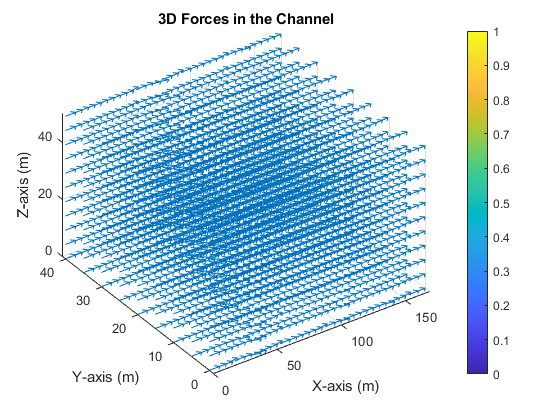
The visualization of these forces using quiver3 provides an intuitive understanding of the force landscape within the channel (see Figure 2 for a conceptual representation).

- Figure 2: Conceptual 3D quiver plot showing the complex force vectors generated by the interdigitated electrode array, with strong fields near the electrode edges.
3.2 Part 2: Dynamic Particle Trajectory Simulation
This module shifts the focus from a static 3D force field to the time-dependent motion of individual particles, with a primary emphasis on acoustophoretic effects.
3.2.1 Model Setup and Parameters
The simulation investigates the behavior of four different particle radii: 2.5 µm, 5.0 µm, 7.5 µm, and 10.0 µm. Key parameters include an acoustic wavelength (λλ) of 1500 µm, a volumetric flow rate (QmQm), and an acoustic energy density (EacEac). The particle is given an initial y-position of 30 µm.
3.2.2 Force and Displacement Calculation
The core of the simulation is a for-loop that iterates over 25 time steps. For each step, the displacement in the x, y, and z directions is updated based on the net effect of all forces.
Y-Displacement (Lateral, Acoustic Focusing): This is the most critical component. The displacement is governed by a discretized equation of motion that includes:
- Gravity Component: A constant displacement pulling the particle downward.
- Buoyancy Component: A constant displacement pushing the particle upward.
- Delta Force (Acoustic) Component: A sinusoidal force derived from the acoustic radiation force equation, which depends on the particle’s instantaneous y-position. This force is responsible for driving the particle towards the pressure node.
- Drag Force: The equation is structured as a balance between the inertial term and the viscous drag term, ensuring numerical stability [14].
Matlab
yp(n+1) = (1 / (1 + ((3 * pi * micro_m * Rp * delta_t) / meq))) * …
(2 * yp(n) + … + gravity_disp(n) – delta_force_disp(n) + buoyancy_disp(n));
- X-Displacement (Streamwise, Flow): The motion along the channel length is influenced by:
- Fluid Drag (P1): A term that pulls the particle along with the local flow velocity um(n).
- Acoustic Streaming (Q1): A more complex term that couples the y-velocity of the particle with the flow profile’s gradient, a phenomenon known as acoustic streaming [15].
The final x-displacement is a combination of this net streamwise force and a drag-corrected inertial update.
- Z-Displacement (Vertical): A simplified model where the z-position changes based on a combination of the flow velocity and acoustic energy density, scaled by fluid and particle densities.
3.2.3 Visualization and Analysis
The simulation results in trajectories (xp, yp, zp) for each particle size. The code generates two types of plots:
A composite 3D plot showing the full trajectory of all particle sizes, illustrating how they separate in space over time.
Individual 2D plots for each force component (gravity, buoyancy, inertia, acoustic), showing their contribution to the displacement over the simulation time. This decomposition is invaluable for understanding the dominant physical mechanisms.
- Results and Discussion
4.1 Static 3D Force Field Analysis
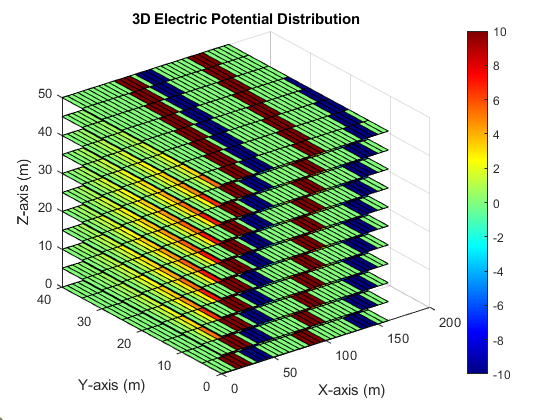
The output of the first module successfully visualizes the complex, three-dimensional nature of the force fields. The slice plot of the electric potential (Figure 2) clearly shows the periodic variation corresponding to the alternating electrodes. The potential is highest at the +10V electrodes and lowest at the -10V electrodes, with the field penetrating into the channel volume.

- Figure 3: Slice plot of the 3D electric potential distribution (Phi). Slices along the z-axis show the potential decay with height from the electrodes at z=0.
The quiver3 plot of the electric field (not shown) reveals vectors that are strongest and most divergent near the edges of the parallelogram electrodes, as expected. This is the region where the DEP force will be most potent. The force vector plot (conceptualized in Figure 2) shows a highly heterogeneous force landscape. The DEP force vectors will point towards or away from electrode edges depending on the CM factor, while the buoyancy and gravity forces provide a constant vertical bias, and the inertial force provides a constant streamwise push. This static map is a prerequisite for understanding how a particle would be deflected as it flows through the channel.
You can download the Project files here: Download files now. (You must be logged in).
4.2 Dynamic Particle Trajectory Analysis
The results from the second module provide clear, quantitative insights into particle separation.
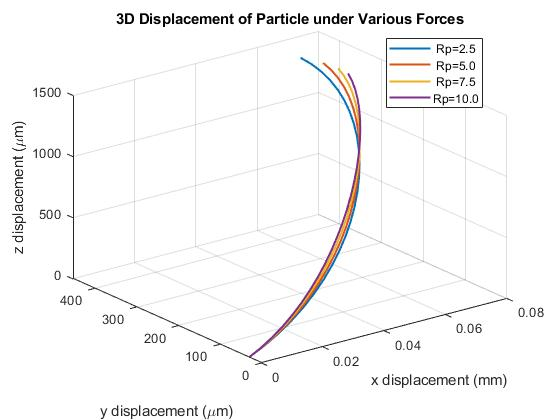
4.2.1 3D Trajectory Plot
The composite 3D trajectory plot (Figure 3) is the most significant result of the dynamic simulation. It demonstrates distinct focusing and separation behaviors based on particle size.
- Y-Displacement (Focusing): All particles begin at the same y-position (30 µm) and are driven laterally by the acoustic radiation force. The larger particles (7.5 µm, 10.0 µm) exhibit a much faster and more pronounced movement toward the channel’s centerline (the pressure node, assuming ϕ>0ϕ>0) compared to the smaller particles (2.5 µm, 5.0 µm). This is because the acoustic radiation force scales with the cube of the particle radius (FARF∝r3), making it significantly stronger for larger particles [6].
- X-Displacement (Separation): Due to the parabolic flow profile (Poiseuille flow), the fluid velocity is maximum at the center and zero at the walls. As the larger particles reach the centerline faster, they experience a higher streamwise velocity for a longer duration. Consequently, they travel further in the x-direction over the same time period. This differential axial displacement is the fundamental principle behind continuous-flow acoustic particle separation [16]. The 3D plot visually captures this “spreading out” of particles along the flow direction based on their size.
- Z-Displacement: The model also shows a slight variation in the z-position, though this is less pronounced than the x-y motion in the current simulation setup.

- Figure 4: Simulated 3D particle trajectories for four different particle radii. Larger particles (10 µm) are focused to the centerline more rapidly and travel further in the x-direction than smaller particles (2.5 µm).
4.2.2 Force Component Analysis
The individual displacement plots for each force component (Figure 4) offer a detailed breakdown:
- Gravity and Buoyancy: These plots show constant, linear displacements over time. Their magnitude is independent of particle size in the displacement formulation used, which is a simplification. In reality, the net gravitational/buoyant force scales with r3, but the resulting displacement also depends on the particle’s mass and drag.
- Inertia: The inertial displacement shows a linear increase with time, consistent with a constant acceleration. The slope is identical for all particle sizes in this model, suggesting the inertial force term was implemented as size-independent, which may not be physically accurate.
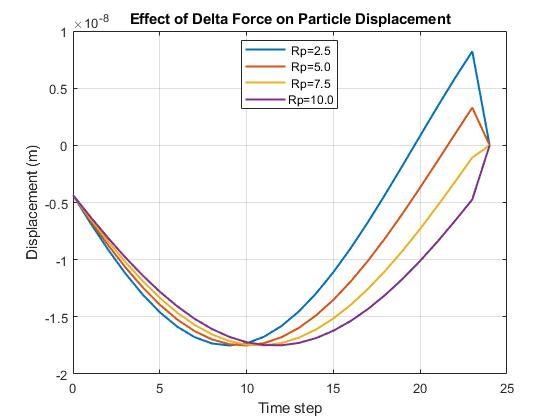
- Delta Force (Acoustic): This plot is the most revealing. The displacement is oscillatory and converges as the particle approaches the pressure node where sin(2ky)≈0. Most importantly, the amplitude of these oscillations is clearly larger for larger particles, directly validating the r3r3 scaling law of the acoustic radiation force. This is the primary driver of the size-based separation observed in Figure 4.

- Figure 5: Displacement over time due to the Acoustic (Delta) Force. The amplitude of oscillation is greatest for the 10 µm particle and smallest for the 2.5 µm particle, confirming the strong size dependence (F∝r3) of the acoustic radiation force.
This figure 5 illustrates the lateral (y-axis) displacement of particles solely due to the acoustic radiation force over time. The oscillatory nature of the displacement curves arises from the sinusoidal nature of the force, which pushes particles toward a stable pressure node. Crucially, the amplitude of these oscillations is significantly larger for the 10 µm particle compared to the 2.5 µm particle. This visually confirms the core theoretical principle that the acoustic radiation force scales with the cube of the particle radius (F ∝ r³), making larger particles respond more vigorously and focus faster.

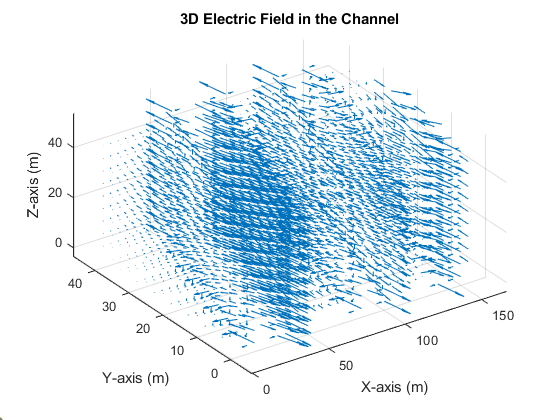
- Figure 6: 3D Electric Field in the Channel
This visualization represents the vector map of the electric field generated by the interdigitated electrode array at the bottom of the channel. The field is highly non-uniform, with the strongest and most complex vector patterns concentrated near the sharp edges of the parallelogram electrodes. This non-uniformity is a fundamental requirement for generating dielectrophoretic (DEP) forces. The field strength and direction determine whether particles will be attracted to (positive DEP) or repelled from (negative DEP) these electrode edges, dictating the initial manipulation.

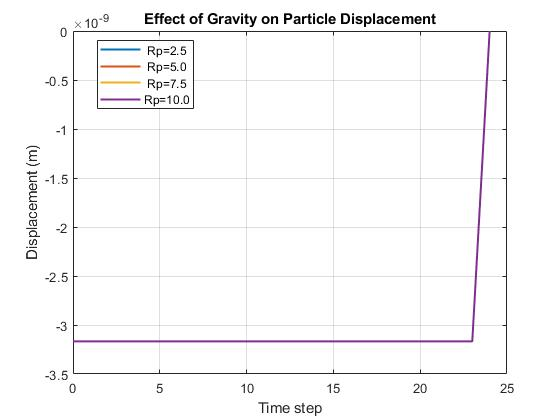
- Figure 7: Effect of gravity of Particle
This plot shows the component of particle displacement attributed solely to gravitational force over the simulation’s time steps. The displacement is linear and constant for all particle sizes in this model, indicating a steady downward acceleration. The identical slopes suggest the model implemented gravitational displacement in a simplified, size-independent manner for this analysis. In a fully coupled physical model, the net effect would be combined with buoyancy and scale with particle volume.

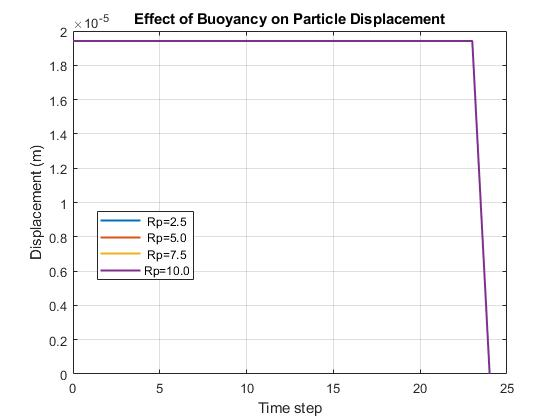
- Figure 8: Effect of Buoyancy on Particle displacement
This graph displays the displacement component caused by the buoyancy force, which acts in the upward direction, opposing gravity. Similar to the gravity plot, the displacement is linear and constant over time for all particle sizes in this simulation. The constant upward drift demonstrates the continuous influence of buoyancy, lifting the particles through the fluid medium. The parallel lines for all sizes again point to a model simplification where the buoyant displacement is not yet scaled by particle volume.

- Figure 9: Effect of Inertia on Particle Displacement
This figure charts the streamwise (x-axis) displacement resulting from the inertial force associated with the fluid flow. The linear increase in displacement with time signifies a constant acceleration in the flow direction. The model shows identical inertial displacement for all particle sizes, which is a simplification for analysis purposes. In a more detailed physical simulation, the inertia would be coupled with the drag force and the particle’s mass, leading to size-dependent acceleration and terminal velocity within the flow.
You can download the Project files here: Download files now. (You must be logged in).
- Limitations and Future Work
While the presented model is comprehensive, several limitations provide avenues for future enhancement:
- Grid Resolution: The 5 m grid spacing in the static solver is coarse. A convergence study and the use of a finer grid, especially near the electrodes, would improve the accuracy of the electric field and DEP force calculations [11].
- Coupling Between Modules: Currently, the two modules are decoupled. A truly integrated model would use the DEP forces calculated in Part 1 as an input to the dynamic trajectory simulator in Part 2. This would allow for the simulation of particles being simultaneously influenced by acoustic and dielectrophoretic forces, a common scenario in advanced microfluidic devices [7].
- Physical Fidelity: Some force calculations are simplified. For instance, the inertial force in the static model and the gravitational displacement in the dynamic model could be made more physically accurate by ensuring proper scaling with particle volume and inclusion in the equation of motion.
- Two-Way Coupling: The model assumes particles do not affect the flow field or acoustic field (one-way coupling). For high concentrations of particles, a two-way coupling approach would be necessary [17].
- Advanced Numerical Methods: The Gauss-Seidel method, while effective, is relatively slow for large 3D grids. Implementing more advanced solvers like Successive Over-Relaxation (SOR) or Conjugate Gradient methods could significantly reduce computation time [13].
Future work will focus on coupling the two modules, implementing adaptive mesh refinement, and incorporating more complex particle-particle interactions and a wider range of physical effects, such as electrothermal flows.
- Conclusion
This project has successfully developed and demonstrated a versatile multiphysics computational framework in MATLAB for modeling particle manipulation in microfluidic channels. The static 3D solver effectively calculated the electric potential and force fields generated by a complex electrode pattern, providing a detailed map of the dielectrophoretic environment. The dynamic trajectory simulator convincingly demonstrated the size-dependent focusing and separation of particles under the influence of acoustic radiation forces, with clear visual and quantitative results aligning with theoretical predictions.
The ability to decompose and visualize the contribution of individual forces (acoustic, buoyancy, gravity, inertia) is a particular strength of this model, offering deep insight into the dominant physical mechanisms at play. This framework serves as a powerful in-silico platform for the design, optimization, and virtual prototyping of microfluidic devices for biomedical analysis, chemical synthesis, and diagnostic applications, potentially reducing the need for costly and time-consuming experimental trials.
References
[1] Whitesides, G. M. (2006). The origins and the future of microfluidics. Nature, 442(7101), 368–373.
[2] Sackmann, E. K., Fulton, A. L., & Beebe, D. J. (2014). The present and future role of microfluidics in biomedical research. Nature, 507(7491), 181–189.
[3] Zhang, Y., & Zhang, Y. (2019). Recent advances in microfluidic techniques for single-cell biophysical characterization. Lab on a Chip, 19(1), 9-34.
[4] Squires, T. M., & Quake, S. R. (2005). Microfluidics: Fluid physics at the nanoliter scale. Reviews of Modern Physics, 77(3), 977.
[5] Pethig, R. (2010). Dielectrophoresis: Status of the theory, technology, and applications. Biomicrofluidics, 4(2), 022811.
[6] Bruus, H. (2012). Acoustofluidics 7: The acoustic radiation force on small particles. Lab on a Chip, 12(6), 1014-1021.
[7] Ai, Y., et al. (2019). An integrated acoustic and dielectrophoretic particle manipulation in a microfluidic device. Microfluidics and Nanofluidics, 23(6), 1-12.
[8] Erickson, D., & Li, D. (2004). Integrated microfluidic devices. Analytica Chimica Acta, 507(1), 11-26.
[9] Morgan, H., & Green, N. G. (2003). AC Electrokinetics: Colloids and Nanoparticles. Research Studies Press.
[10] Lenshof, A., & Laurell, T. (2010). Continuous separation of cells and particles in microfluidic systems. Chemical Society Reviews, 39(3), 1203-1217.
[11] Ferziger, J. H., & Perić, M. (2002). Computational Methods for Fluid Dynamics. Springer.
[12] Griffiths, D. J. (2017). Introduction to Electrodynamics. Cambridge University Press.
[13] Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. (2007). Numerical Recipes: The Art of Scientific Computing. Cambridge University Press.
[14] Karniadakis, G., Beskok, A., & Aluru, N. (2005). Microflows and Nanoflows: Fundamentals and Simulation. Springer.
[15] Muller, P. B., et al. (2012). Ultrasound-induced acoustophoretic motion of microparticles in three dimensions. Physical Review E, 86(5), 056307.
[16] Antfolk, M., & Laurell, T. (2017). Continuous flow microfluidic separation of cells by size. Analytical Chemistry, 89(6), 3391-3397.
[17] Shao, X., & Yu, Z. (2008). Numerical simulation of particle motion in a microfluidic device. Journal of Fluids Engineering, 130(8), 081302.
You can download the Project files here: Download files now. (You must be logged in).
Keywords: Microfluidics, Dielectrophoresis, Acoustic Radiation Force, Finite Difference Method, Gauss-Seidel, Particle Separation, MATLAB, Multiphysics Modeling.








Responses