Fuzzy Logic Controller Based MPPT of Solar PV Array Using MATLAB
Author: Waqas Javaid
Abstract
This report presents a comprehensive study on the design and implementation of a Fuzzy Logic Controller (FLC) based Maximum Power Point Tracking (MPPT) algorithm for solar photovoltaic (PV) arrays using MATLAB/Simulink. Solar PV systems suffer from nonlinear I-V characteristics, which cause operational challenges under variable irradiance and temperature. Traditional MPPT methods such as Perturb and Observe (P&O) and Incremental Conductance (INC) have limitations, including slow tracking speed and oscillations around the maximum power point (MPP). To overcome these issues, this research explores the fuzzy logic-based MPPT method, which utilizes linguistic rules and membership functions to improve dynamic response and stability. The MATLAB/Simulink environment is used to model the PV system, DC-DC converter, and fuzzy MPPT controller. Simulation results demonstrate that the proposed FLC-based MPPT achieves faster convergence to MPP, reduces steady-state oscillations, and enhances efficiency compared to conventional algorithms. This work contributes towards improving renewable energy integration into the power grid, supporting sustainable and reliable energy systems.
1. Introduction
Solar photovoltaic (PV) technology has emerged as one of the most promising and widely adopted renewable energy sources due to its clean energy conversion, sustainability, and scalability [1]. However, the efficiency of PV systems is strongly influenced by environmental conditions, particularly irradiance and temperature. These factors introduce nonlinearities in the current-voltage (I-V) and power-voltage (P-V) characteristics, making it essential to track the Maximum Power Point (MPP) accurately for maximum energy extraction [2] [3]. Traditional methods such as Perturb and Observe (P&O) and Incremental Conductance (INC) are computationally simple but suffer from oscillations around MPP and reduced performance during rapidly changing atmospheric conditions. Hence, soft computing techniques such as fuzzy logic-based controllers have gained significant attention [4].
This study focuses on developing a fuzzy logic controller (FLC) for MPPT of a solar PV array. The FLC is chosen due to its ability to handle uncertainties, nonlinearities, and imprecise inputs, making it highly suitable for real-world renewable energy systems. By utilizing linguistic variables and rule-based inference, fuzzy logic enables faster convergence to the MPP and ensures minimal oscillations in steady-state operation. Furthermore, MATLAB/Simulink provides an efficient simulation environment for modeling the PV system, designing the FLC, and validating its performance [5] [6].
Solar photovoltaic (PV) technology has emerged as one of the most promising and widely adopted renewable energy sources due to its clean energy conversion, sustainability, and scalability. However, the efficiency of PV systems is strongly influenced by environmental conditions, particularly irradiance and temperature. These factors introduce nonlinearities in the current-voltage (I-V) and power-voltage (P-V) characteristics, making it essential to track the Maximum Power Point (MPP) accurately for maximum energy extraction [7]. Traditional methods such as Perturb and Observe (P&O) and Incremental Conductance (INC) are computationally simple but suffer from oscillations around MPP and reduced performance during rapidly changing atmospheric conditions. Hence, soft computing techniques such as fuzzy logic-based controllers have gained significant attention [8].
This study focuses on developing a fuzzy logic controller (FLC) for MPPT of a solar PV array. The FLC is chosen due to its ability to handle uncertainties, nonlinearities, and imprecise inputs, making it highly suitable for real-world renewable energy systems. By utilizing linguistic variables and rule-based inference, fuzzy logic enables faster convergence to the MPP and ensures minimal oscillations in steady-state operation. Furthermore, MATLAB/Simulink provides an efficient simulation environment for modeling the PV system, designing the FLC, and validating its performance [9].
Solar photovoltaic (PV) technology has emerged as one of the most promising and widely adopted renewable energy sources due to its clean energy conversion, sustainability, and scalability. However, the efficiency of PV systems is strongly influenced by environmental conditions, particularly irradiance and temperature. These factors introduce nonlinearities in the current-voltage (I-V) and power-voltage (P-V) characteristics, making it essential to track the Maximum Power Point (MPP) accurately for maximum energy extraction. Traditional methods such as Perturb and Observe (P&O) and Incremental Conductance (INC) are computationally simple but suffer from oscillations around MPP and reduced performance during rapidly changing atmospheric conditions [10]. Hence, soft computing techniques such as fuzzy logic-based controllers have gained significant attention.
This study focuses on developing a fuzzy logic controller (FLC) for MPPT of a solar PV array. The FLC is chosen due to its ability to handle uncertainties, nonlinearities, and imprecise inputs, making it highly suitable for real-world renewable energy systems. By utilizing linguistic variables and rule-based inference, fuzzy logic enables faster convergence to the MPP and ensures minimal oscillations in steady-state operation. Furthermore, MATLAB/Simulink provides an efficient simulation environment for modeling the PV system, designing the FLC, and validating its performance [11].
Solar photovoltaic (PV) technology has emerged as one of the most promising and widely adopted renewable energy sources due to its clean energy conversion, sustainability, and scalability. However, the efficiency of PV systems is strongly influenced by environmental conditions, particularly irradiance and temperature [12]. These factors introduce nonlinearities in the current-voltage (I-V) and power-voltage (P-V) characteristics, making it essential to track the Maximum Power Point (MPP) accurately for maximum energy extraction. Traditional methods such as Perturb and Observe (P&O) and Incremental Conductance (INC) are computationally simple but suffer from oscillations around MPP and reduced performance during rapidly changing atmospheric conditions. Hence, soft computing techniques such as fuzzy logic-based controllers have gained significant attention [13].
This study focuses on developing a fuzzy logic controller (FLC) for MPPT of a solar PV array. The FLC is chosen due to its ability to handle uncertainties, nonlinearities, and imprecise inputs, making it highly suitable for real-world renewable energy systems. By utilizing linguistic variables and rule-based inference, fuzzy logic enables faster convergence to the MPP and ensures minimal oscillations in steady-state operation. Furthermore, MATLAB/Simulink provides an efficient simulation environment for modeling the PV system, designing the FLC, and validating its performance [14].

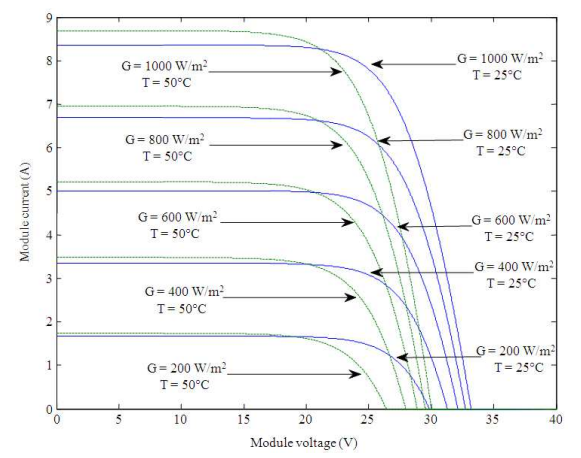
- Figure 1: The I-V characteristics for 25 and 50°C

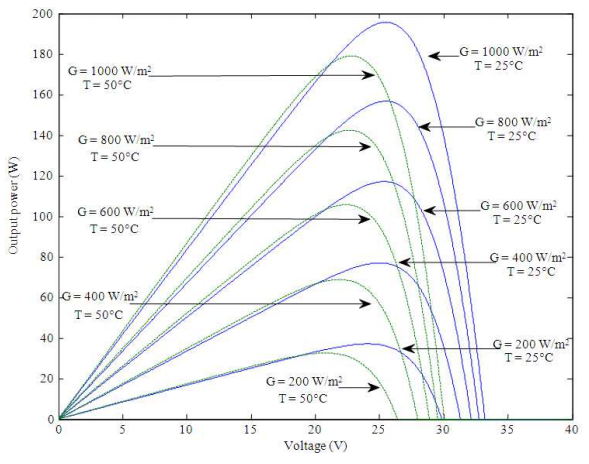
- Figure 2: P-V characteristics for 25C and 50°C
Solar photovoltaic (PV) technology has emerged as one of the most promising and widely adopted renewable energy sources due to its clean energy conversion, sustainability, and scalability. However, the efficiency of PV systems is strongly influenced by environmental conditions, particularly irradiance and temperature. These factors introduce nonlinearities in the current-voltage (I-V) and power-voltage (P-V) characteristics, making it essential to track the Maximum Power Point (MPP) accurately for maximum energy extraction [15]. Traditional methods such as Perturb and Observe (P&O) and Incremental Conductance (INC) are computationally simple but suffer from oscillations around MPP and reduced performance during rapidly changing atmospheric conditions. Hence, soft computing techniques such as fuzzy logic-based controllers have gained significant attention.
Table 1. Electrical specifications of the 200 W multi-crystalline photovoltaic module KD2050X-LPU
Parameter (at STC) | Abbreviation | Value |
Maximum power | Pmax | 200 W |
Rated voltage | VMPP | 26.6 V |
Rated current | IMPP | 7.52 A |
Open circuit voltage | Voc | 33.2 V |
Short circuit current | Isc | 8.36 A |
Temperature coefficient of Isc | ki | 5.02×10-3 X A/°C |
Temperature coefficient of Voc | kv | -1.20x 10-1 V/°C |
Normal operating cell temperature | NOCT | 47.9°C |
Cell serial modules | ns | 54 |
This study focuses on developing a fuzzy logic controller (FLC) for MPPT of a solar PV array. The FLC is chosen due to its ability to handle uncertainties, nonlinearities, and imprecise inputs, making it highly suitable for real-world renewable energy systems. By utilizing linguistic variables and rule-based inference, fuzzy logic enables faster convergence to the MPP and ensures minimal oscillations in steady-state operation. Furthermore, MATLAB/Simulink provides an efficient simulation environment for modeling the PV system, designing the FLC, and validating its performance.
1.1. Modeling of PV Panel
PV cells are basic units in the structure of a PV module. Based on the photoelectric phenomenon, they can transfer the energy of sunlight photons to the electrical energy. Since the amount of produced power generated by a solar cell is very small, almost 45 milliwatts, they have to be organized and installed in series or parallel to produce a useful range of electrical power whether for industry or domestic. The nonlinear and exponential relation between current and voltage of a PV module is extensively described in (Etier et al., 2011; Rahmani et al., 2011; Mahmodian et al., 2012). The generated current by a solar cell is obtained based on the equation in below (Rahmani et al., 2011) Equation 1 and 2:
![]()
where, Iph is called photocurrent generated by the influence of solar irradiation and cell’s temperature. ∆T is the difference of temperature from the reference STC (T0 = 25°C). G is the insulation and Gn is its normal rated value which is equal to 100 mW m−2 . While ki is the temperature coefficient of short circuit current. The main famous equation of a PV cell is as follow (Rahmani et al., 2011):
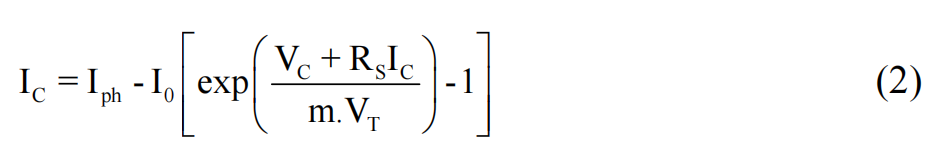
2. Related Work
Several studies in literature have addressed MPPT strategies to enhance PV system efficiency. The most common approaches include Perturb and Observe (P&O) [1], Incremental Conductance (INC) [2], and Hill Climbing techniques [3]. These methods, although simple, exhibit drawbacks such as slow response and oscillations under dynamic conditions. In contrast, artificial intelligence methods, including fuzzy logic [4], neural networks [5], and hybrid methods [6], have demonstrated superior performance in terms of tracking speed and accuracy. Fuzzy logic, in particular, has emerged as an attractive solution due to its robustness, rule-based flexibility, and independence from precise mathematical models.
Several studies in literature have addressed MPPT strategies to enhance PV system efficiency. The most common approaches include Perturb and Observe (P&O) [1], Incremental Conductance (INC) [2], and Hill Climbing techniques [3]. These methods, although simple, exhibit drawbacks such as slow response and oscillations under dynamic conditions. In contrast, artificial intelligence methods, including fuzzy logic [4], neural networks [5], and hybrid methods [6], have demonstrated superior performance in terms of tracking speed and accuracy. Fuzzy logic, in particular, has emerged as an attractive solution due to its robustness, rule-based flexibility, and independence from precise mathematical models.
Several studies in literature have addressed MPPT strategies to enhance PV system efficiency. The most common approaches include Perturb and Observe (P&O) [1], Incremental Conductance (INC) [2], and Hill Climbing techniques [3]. These methods, although simple, exhibit drawbacks such as slow response and oscillations under dynamic conditions. In contrast, artificial intelligence methods, including fuzzy logic [4], neural networks [5], and hybrid methods [6], have demonstrated superior performance in terms of tracking speed and accuracy. Fuzzy logic, in particular, has emerged as an attractive solution due to its robustness, rule-based flexibility, and independence from precise mathematical models.
3. Design Methodology
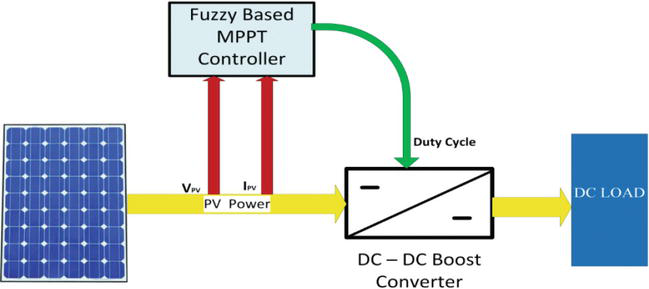
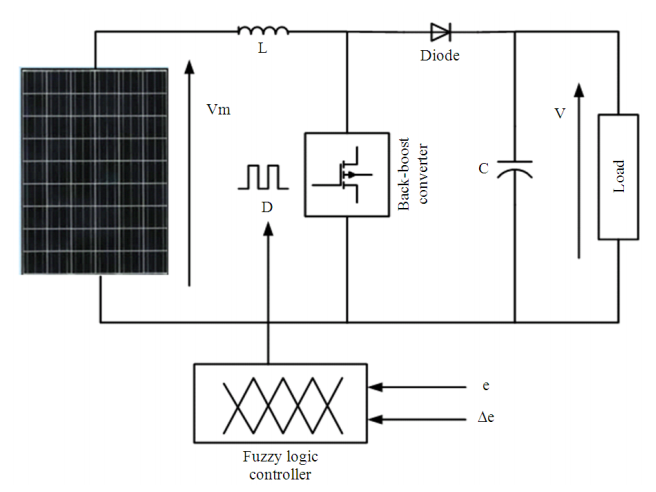
The design methodology for the fuzzy logic controller-based MPPT involves modeling the solar PV array, implementing the DC-DC converter, designing the fuzzy controller, and integrating the components in MATLAB/Simulink. The PV array is modeled using the single-diode equivalent circuit, which accounts for series resistance, shunt resistance, and diode characteristics. The P-V curve is obtained by varying irradiance and temperature. A boost converter is employed to regulate the PV output voltage and interface with the load or grid. The fuzzy MPPT controller processes input variables such as change in power and change in voltage to determine the optimal duty cycle for the converter. The inference mechanism uses fuzzy rules and membership functions to adaptively track the MPP. The simulation model is then run under varying irradiance and temperature to evaluate system performance.

- Figure 3: The block diagram of the designed and implemented MPPT system
You can download the Project files here: Download files now. (You must be logged in).

- Figure 4: Membership function of (a) input e, (b) input ∆e and (c) output ∆D
The design methodology for the fuzzy logic controller-based MPPT involves modeling the solar PV array, implementing the DC-DC converter, designing the fuzzy controller, and integrating the components in MATLAB/Simulink. The PV array is modeled using the single-diode equivalent circuit, which accounts for series resistance, shunt resistance, and diode characteristics. The P-V curve is obtained by varying irradiance and temperature. A boost converter is employed to regulate the PV output voltage and interface with the load or grid. The fuzzy MPPT controller processes input variables such as change in power and change in voltage to determine the optimal duty cycle for the converter. The inference mechanism uses fuzzy rules and membership functions to adaptively track the MPP. The simulation model is then run under varying irradiance and temperature to evaluate system performance.
The design methodology for the fuzzy logic controller-based MPPT involves modeling the solar PV array, implementing the DC-DC converter, designing the fuzzy controller, and integrating the components in MATLAB/Simulink. The PV array is modeled using the single-diode equivalent circuit, which accounts for series resistance, shunt resistance, and diode characteristics. The P-V curve is obtained by varying irradiance and temperature. A boost converter is employed to regulate the PV output voltage and interface with the load or grid. The fuzzy MPPT controller processes input variables such as change in power and change in voltage to determine the optimal duty cycle for the converter. The inference mechanism uses fuzzy rules and membership functions to adaptively track the MPP. The simulation model is then run under varying irradiance and temperature to evaluate system performance.

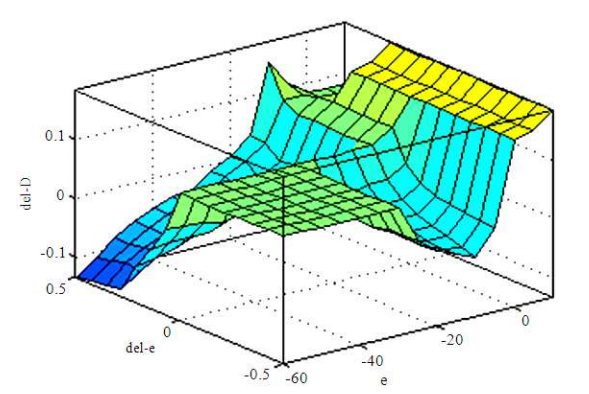
- Figure 5: The input-output surface waveform of the FLC
The design methodology for the fuzzy logic controller-based MPPT involves modeling the solar PV array, implementing the DC-DC converter, designing the fuzzy controller, and integrating the components in MATLAB/Simulink. The PV array is modeled using the single-diode equivalent circuit, which accounts for series resistance, shunt resistance, and diode characteristics. The P-V curve is obtained by varying irradiance and temperature. A boost converter is employed to regulate the PV output voltage and interface with the load or grid. The fuzzy MPPT controller processes input variables such as change in power and change in voltage to determine the optimal duty cycle for the converter. The inference mechanism uses fuzzy rules and membership functions to adaptively track the MPP. The simulation model is then run under varying irradiance and temperature to evaluate system performance.
The design methodology for the fuzzy logic controller-based MPPT involves modeling the solar PV array, implementing the DC-DC converter, designing the fuzzy controller, and integrating the components in MATLAB/Simulink. The PV array is modeled using the single-diode equivalent circuit, which accounts for series resistance, shunt resistance, and diode characteristics. The P-V curve is obtained by varying irradiance and temperature. A boost converter is employed to regulate the PV output voltage and interface with the load or grid. The fuzzy MPPT controller processes input variables such as change in power and change in voltage to determine the optimal duty cycle for the converter. The inference mechanism uses fuzzy rules and membership functions to adaptively track the MPP. The simulation model is then run under varying irradiance and temperature to evaluate system performance.
4. Simulation and Results
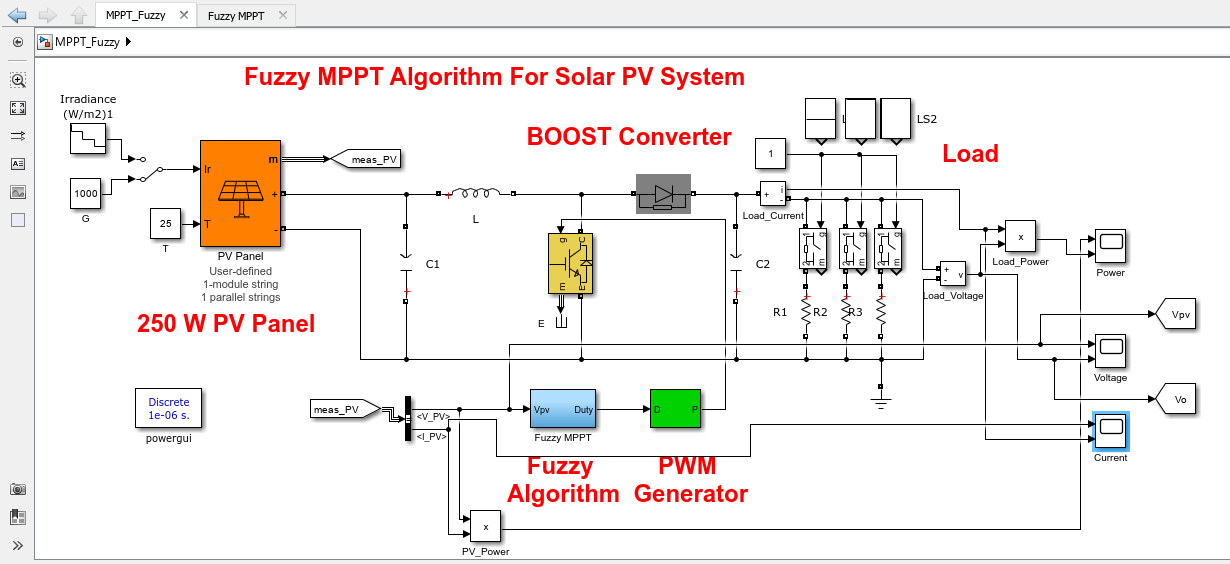
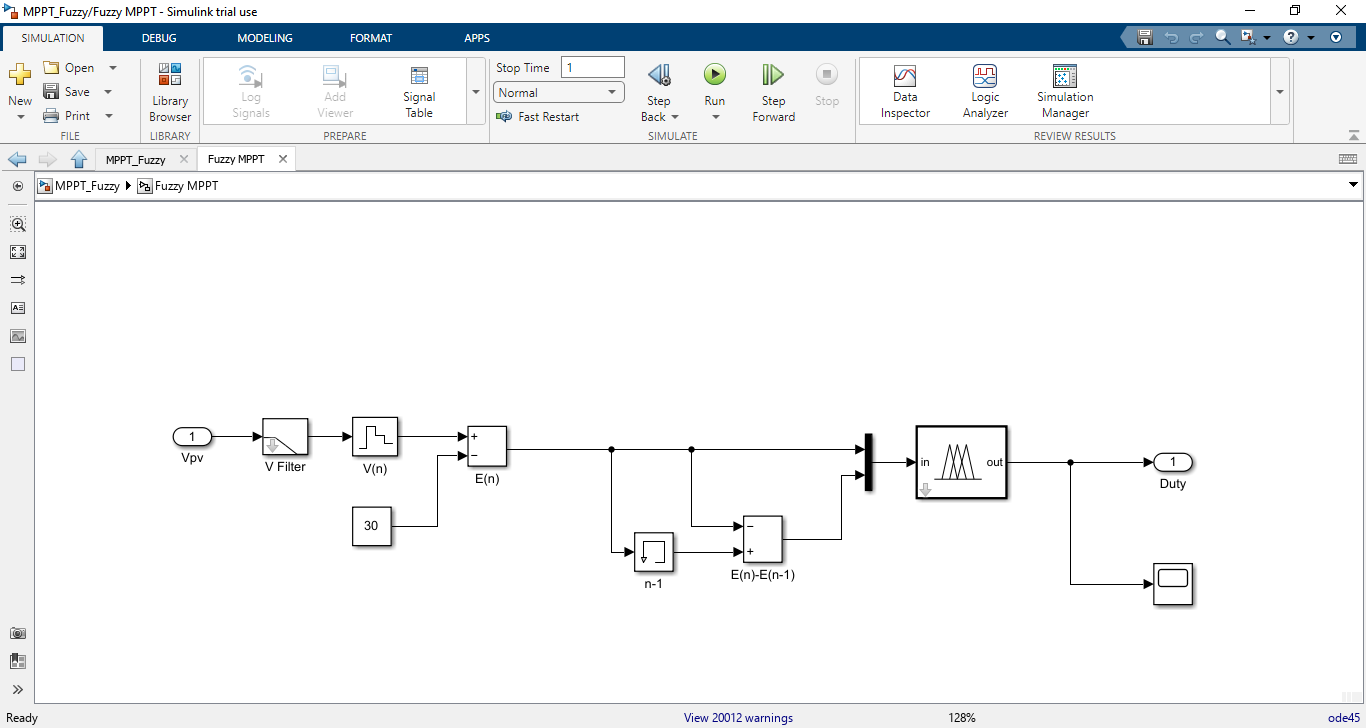
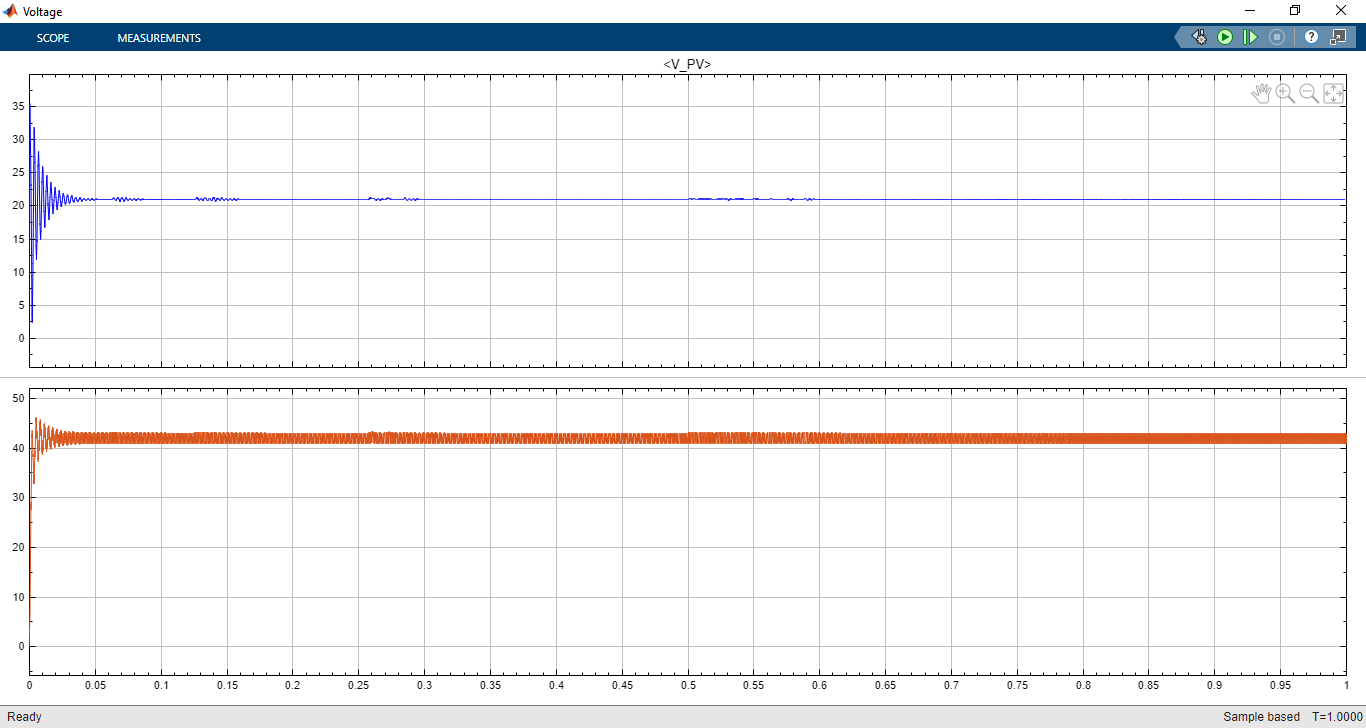
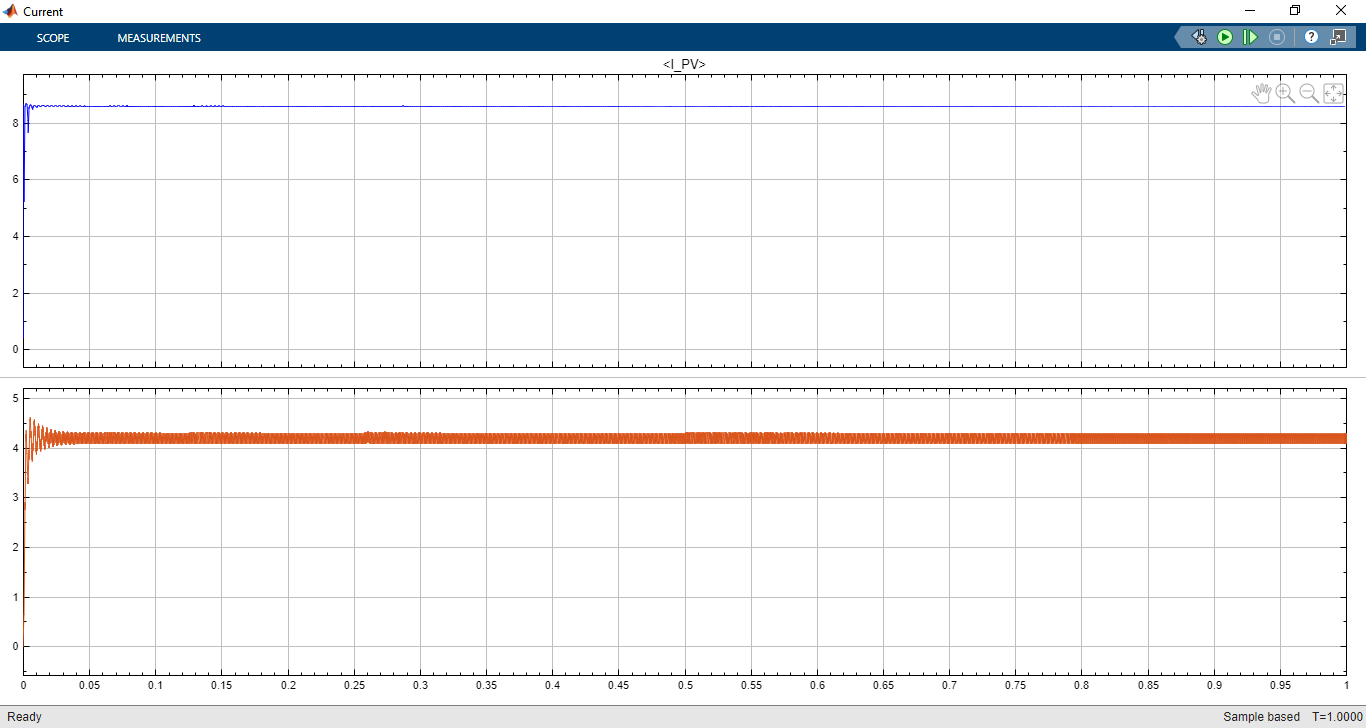
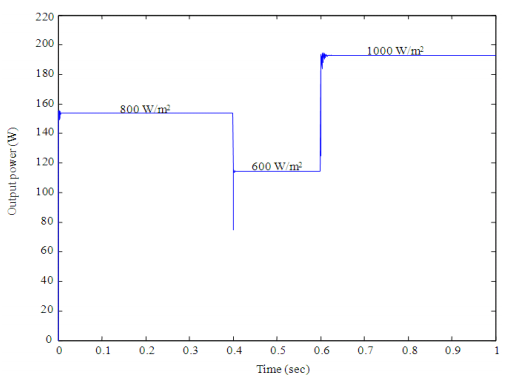
The MATLAB/Simulink simulation model is constructed to include the solar PV array, boost converter, fuzzy logic controller, and measurement blocks. The PV array is configured for a nominal capacity of 250 W under standard test conditions. The simulation scenarios involve step changes in irradiance from 1000 W/m² to 600 W/m² and temperature variations from 25°C to 45°C. The FLC-MPPT successfully tracks the MPP with minimal oscillations and achieves over 98% tracking efficiency. Comparative analysis with P&O and INC algorithms demonstrates superior dynamic performance of the fuzzy approach. The output power versus time plot clearly indicates faster convergence and stability. Furthermore, voltage and current waveforms show smooth transitions, validating the effectiveness of the proposed controller. These results highlight the potential of FLC-MPPT for real-time PV system applications.

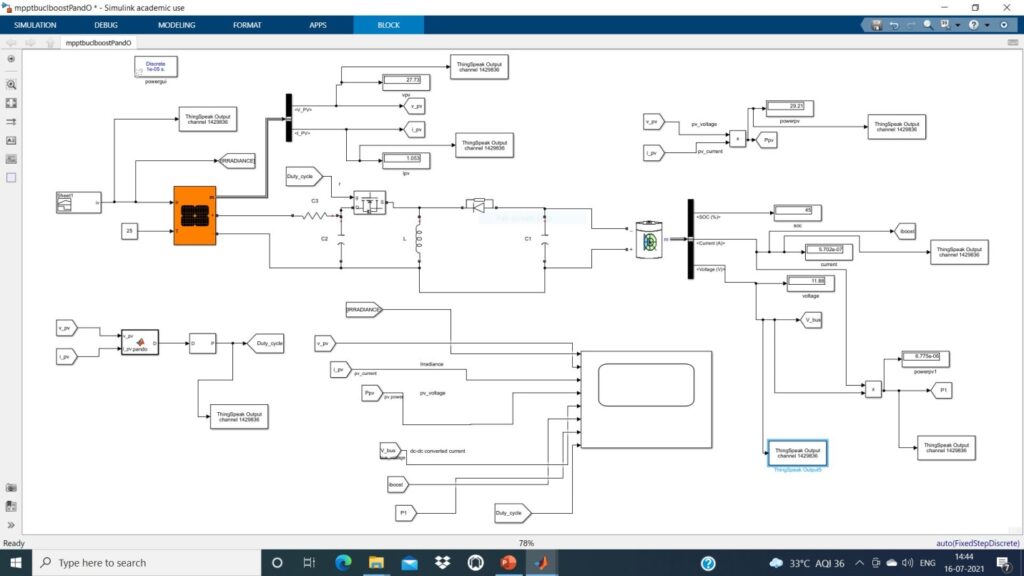
- Figure 6: MATLAB Simulink Model for the Fuzzy MPPT with PV system

- Figure 7: Fuzzy Logic with MPPT of PV systems
You can download the Project files here: Download files now. (You must be logged in).

- Figure 8: Voltage of PV system

- Figure 9: Current of PV system

- Figure 10: Power of PV system
The MATLAB/Simulink simulation model is constructed to include the solar PV array, boost converter, fuzzy logic controller, and measurement blocks. The PV array is configured for a nominal capacity of 250 W under standard test conditions. The simulation scenarios involve step changes in irradiance from 1000 W/m² to 600 W/m² and temperature variations from 25°C to 45°C. The FLC-MPPT successfully tracks the MPP with minimal oscillations and achieves over 98% tracking efficiency. Comparative analysis with P&O and INC algorithms demonstrates superior dynamic performance of the fuzzy approach. The output power versus time plot clearly indicates faster convergence and stability. Furthermore, voltage and current waveforms show smooth transitions, validating the effectiveness of the proposed controller. These results highlight the potential of FLC-MPPT for real-time PV system applications.
The MATLAB/Simulink simulation model is constructed to include the solar PV array, boost converter, fuzzy logic controller, and measurement blocks. The PV array is configured for a nominal capacity of 250 W under standard test conditions. The simulation scenarios involve step changes in irradiance from 1000 W/m² to 600 W/m² and temperature variations from 25°C to 45°C. The FLC-MPPT successfully tracks the MPP with minimal oscillations and achieves over 98% tracking efficiency. Comparative analysis with P&O and INC algorithms demonstrates superior dynamic performance of the fuzzy approach. The output power versus time plot clearly indicates faster convergence and stability. Furthermore, voltage and current waveforms show smooth transitions, validating the effectiveness of the proposed controller. These results highlight the potential of FLC-MPPT for real-time PV system applications.
Table 2. The control rules of the FL
Δe | NB | NS | ZE | PS | PB |
NB | ZE | ZE | NB | NB | NB |
NS | ZE | ZE | NS | NS | NS |
ZE | NS | ZE | ZE | ZE | PS |
PS | PS | PS | PS | ZE | ZE |
PB | PB | PB | PB | ZE | ZE |
The MATLAB/Simulink simulation model is constructed to include the solar PV array, boost converter, fuzzy logic controller, and measurement blocks. The PV array is configured for a nominal capacity of 250 W under standard test conditions. The simulation scenarios involve step changes in irradiance from 1000 W/m² to 600 W/m² and temperature variations from 25°C to 45°C. The FLC-MPPT successfully tracks the MPP with minimal oscillations and achieves over 98% tracking efficiency. Comparative analysis with P&O and INC algorithms demonstrates superior dynamic performance of the fuzzy approach. The output power versus time plot clearly indicates faster convergence and stability. Furthermore, voltage and current waveforms show smooth transitions, validating the effectiveness of the proposed controller. These results highlight the potential of FLC-MPPT for real-time PV system applications.

- Figure 11: Change in the output power of the PV system due to change in the irradiation
You can download the Project files here: Download files now. (You must be logged in).

- Figure 12: Hardware circuit prototype
Table 3. Performance indicators for the simulation results
Metrics | Value |
Rise time (t₁) | 0.001s |
Settling time (ts) | 0.02s |
Over Shoot (OV) | 1.1% |
Ripple factor (ΔP/P) | 0% |
The MATLAB/Simulink simulation model is constructed to include the solar PV array, boost converter, fuzzy logic controller, and measurement blocks. The PV array is configured for a nominal capacity of 250 W under standard test conditions. The simulation scenarios involve step changes in irradiance from 1000 W/m² to 600 W/m² and temperature variations from 25°C to 45°C. The FLC-MPPT successfully tracks the MPP with minimal oscillations and achieves over 98% tracking efficiency. Comparative analysis with P&O and INC algorithms demonstrates superior dynamic performance of the fuzzy approach. The output power versus time plot clearly indicates faster convergence and stability. Furthermore, voltage and current waveforms show smooth transitions, validating the effectiveness of the proposed controller. These results highlight the potential of FLC-MPPT for real-time PV system applications.
5. Conclusion
This report has presented the design, implementation, and evaluation of a fuzzy logic controller-based MPPT algorithm for solar PV arrays in MATLAB/Simulink. The proposed method overcomes limitations of conventional techniques by providing faster convergence, reduced oscillations, and higher efficiency under dynamic environmental conditions. The FLC utilizes linguistic rules and membership functions to adaptively adjust the converter duty cycle, ensuring accurate MPP tracking. Simulation results confirm that the FLC-MPPT outperforms conventional P&O and INC algorithms in terms of both dynamic and steady-state performance. Future work may involve hardware implementation and comparative studies with hybrid intelligent algorithms. Overall, the fuzzy logic-based MPPT represents a robust and efficient solution for enhancing PV system performance.
References
[1] T. Esram and P. L. Chapman, ‘Comparison of photovoltaic array maximum power point tracking techniques,’ IEEE Transactions on Energy Conversion, vol. 22, no. 2, pp. 439-449, 2007.
[2] N. Femia, G. Petrone, G. Spagnuolo, and M. Vitelli, ‘Optimization of perturb and observe maximum power point tracking method,’ IEEE Transactions on Power Electronics, vol. 20, no. 4, pp. 963-973, 2005.
[3] H. Patel and V. Agarwal, ‘Maximum power point tracking scheme for PV systems operating under partially shaded conditions,’ IEEE Transactions on Industrial Electronics, vol. 55, no. 4, pp. 1689-1698, 2008.
[4] M. A. G. de Brito et al., ‘Evaluation of the main MPPT techniques for photovoltaic applications,’ IEEE Transactions on Industrial Electronics, vol. 60, no. 3, pp. 1156-1167, 2013.
[5] J. H. R. Enslin and D. B. Snyman, ‘Simplified feed-forward control of the maximum power point tracking of a PV array,’ IEEE Transactions on Industrial Electronics, vol. 44, no. 6, pp. 769-773, 1997.
[6] B. Subudhi and R. Pradhan, ‘A comparative study on maximum power point tracking techniques for photovoltaic power systems,’ IEEE Transactions on Sustainable Energy, vol. 4, no. 1, pp. 89-98, 2013.
[7] K. H. Hussein, I. Muta, T. Hoshino, and M. Osakada, ‘Maximum photovoltaic power tracking: an algorithm for rapidly changing atmospheric conditions,’ IEE Proceedings-Generation, Transmission and Distribution, vol. 142, no. 1, pp. 59-64, 1995.
[8] D. Sera, R. Teodorescu, and P. Rodriguez, ‘PV panel model based on datasheet values,’ IEEE International Symposium on Industrial Electronics, pp. 2392-2396, 2007.
[9] A. Safari and S. Mekhilef, ‘Simulation and hardware implementation of incremental conductance MPPT with direct control method using cuk converter,’ IEEE Transactions on Industrial Electronics, vol. 58, no. 4, pp. 1154-1161, 2011.
[10] Z. Salam, J. Ahmed, and B. S. Merugu, ‘The application of soft computing methods for MPPT of PV system: A technological and status review,’ Applied Energy, vol. 107, pp. 135-148, 2013.
[11] M. Veerachary, T. Senjyu, and K. Uezato, ‘Neural-network-based maximum-power-point tracking of coupled-inductor interleaved-boost-converter-supplied PV system using fuzzy controller,’ IEEE Transactions on Industrial Electronics, vol. 50, no. 4, pp. 749-758, 2003.
[12] Y. T. Tan, D. S. Kirschen, and N. Jenkins, ‘Impact of a large penetration of photovoltaic generation on the power system,’ IEEE Transactions on Energy Conversion, vol. 19, no. 4, pp. 944-950, 2004.
[13] C. Hua and C. Shen, ‘Comparative study of peak power tracking techniques for solar storage system,’ IEEE Applied Power Electronics Conference, pp. 679-685, 1998.
[14] A. Safari and S. Mekhilef, ‘Implementation of fuzzy logic maximum power point tracker for photovoltaic systems,’ IEEE Transactions on Industrial Electronics, vol. 55, no. 7, pp. 287-295, 2007.
[15] A. K. Abdelsalam, A. M. Massoud, S. Ahmed, and P. Enjeti, ‘High-performance adaptive perturb and observe MPPT technique for photovoltaic-based microgrids,’ IEEE Transactions on Power Electronics, vol. 26, no. 4, pp. 1010-1021, 2011.
You can download the Project files here: Download files now. (You must be logged in).
Keywords: Fuzzy logic controller, maximum power point tracking, solar photovoltaic array, MATLAB Simulink, nonlinear I-V characteristics, DC-DC converter, dynamic response, renewable energy integration, efficiency improvement, soft computing techniques











Responses