Implementation and Evaluation of Sparse Adaptive Filters for Active Noise Control Systems in Matlab
Author : Waqas Javaid
Abstract:
This paper presents the implementation and evaluation of sparse adaptive filters for active noise control (ANC) systems, targeting broadband noise cancellation. We investigate the performance of three adaptive algorithms. Filtered-x Normalized Least Mean Square (FxNLMS), Zero-Attracting FxNLMS (FxNLMS_ZA), and Proportionate NLMS (PNLMS). These algorithms exploit sparsity in the adaptive filter coefficients to improve convergence and noise reduction. Active noise control (ANC) was first comprehensively formulated using adaptive filtering concepts to suppress unwanted acoustic disturbances [1]. A simulation study is conducted to compare the performance of these algorithms in terms of noise cancellation, convergence speed, and filter sparsity. A detailed tutorial on the principles, practical implementations, and stability issues of ANC systems is presented in [2] Results show that sparse adaptive filters achieve significant noise reduction and improved convergence compared to traditional methods. The FxNLMS_ZA algorithm demonstrates superior performance in terms of sparsity and noise cancellation. The PNLMS algorithm shows fast convergence but increased computational complexity. This study provides insights into the design and implementation of efficient ANC systems using sparse adaptive filters. The theoretical basis of adaptive signal processing and LMS-type algorithms was established by Widrow and Stearns in their classic text [3]. The algorithms are tested on a broadband noise signal and their performance is evaluated using metrics such as error power, filter coefficient evolution, and sparsity.
- Introduction:
Active noise control (ANC) systems have become increasingly important in various applications, including industrial noise cancellation, automotive noise reduction, and audio noise cancellation. The primary goal of ANC systems is to reduce unwanted noise by generating an “anti-noise” signal that destructively interferes with the original noise.

- Figure 1: ANC System.
Further extensions to adaptive filter theory, convergence analysis, and system identification are thoroughly discussed by Haykin in [4]. Traditional ANC systems employ adaptive filters, such as the Filtered-x Least Mean Square (FxLMS) algorithm, to generate the anti-noise signal. However, these algorithms often suffer from slow convergence and poor noise reduction performance, particularly in broadband noise environments. Recent research has focused on exploiting sparsity in adaptive filter coefficients to improve ANC performance. Sparse adaptive filters, such as the Filtered-x Normalized Least Mean Square (FxNLMS) algorithm, Zero-Attracting FxNLMS (FxNLMS_ZA), and Proportionate NLMS (PNLMS), have shown promise in achieving improved noise reduction and convergence speed. This paper presents the implementation and evaluation of these sparse adaptive filters for ANC systems, targeting broadband noise cancellation. We investigate the performance of these algorithms in terms of noise cancellation, convergence speed, and filter sparsity. Proportionate normalized LMS (PNLMS) algorithms were developed to speed convergence for sparse systems, particularly in acoustic echo cancellation applications [5]. The algorithms are tested on a broadband noise signal and their performance is evaluated using metrics such as error power, filter coefficient evolution, and sparsity. Our results show that sparse adaptive filters achieve significant noise reduction and improved convergence compared to traditional methods. The FxNLMS_ZA algorithm demonstrates superior performance in terms of sparsity and noise cancellation. The PNLMS algorithm shows fast convergence but increased computational complexity. This study provides insights into the design and implementation of efficient ANC systems using sparse adaptive filters. Zero-attracting and sparse-promoting LMS variants have demonstrated improved performance in sparse channel estimation and motivated sparsity-aware ANC methods [6]. The use of sparse adaptive filters has the potential to significantly improve ANC performance in various applications. Further research is needed to explore the application of these algorithms in real-time ANC systems.
1.1 ANC Systems:
Active noise control (ANC) systems have become increasingly important in various applications, including industrial noise cancellation, automotive noise reduction, and audio noise cancellation. The primary goal of ANC systems is to reduce unwanted noise by generating an “anti-noise” signal that destructively interferes with the original noise. ANC systems typically employ adaptive filters to generate the anti-noise signal. Efficient techniques for subspace tracking and iterative estimation, relevant to fast adaptive updates, were proposed by Martin [7]. These adaptive filters use algorithms such as the Filtered-x Least Mean Square (FxLMS) to adapt to changing noise environments. However, these algorithms often suffer from slow convergence and poor noise reduction performance. This is particularly true in broadband noise environments where the noise signal is complex and non-stationary. To address these limitations, researchers have explored the use of sparse adaptive filters. Adaptive filter ensembles formed through convex combinations have shown improved convergence and robustness in dynamic environments [8]. Sparse adaptive filters exploit the inherent sparsity in the noise signal to improve noise reduction and convergence speed. The use of sparse adaptive filters has the potential to significantly improve ANC performance.
1.2 Limitations of Traditional ANC Systems:
Traditional ANC systems employ adaptive filters, such as the Filtered-x Least Mean Square (FxLMS) algorithm, to generate the anti-noise signal. However, these algorithms often suffer from slow convergence and poor noise reduction performance. This is particularly true in broadband noise environments where the noise signal is complex and non-stationary. Zero-attracting and sparse-promoting LMS variants have demonstrated improved performance in sparse channel estimation and motivated sparsity-aware ANC methods [9]. The FxLMS algorithm is sensitive to the choice of step-size and filter length, which can lead to suboptimal performance. Additionally, the FxLMS algorithm does not take into account the sparsity of the noise signal, which can lead to inefficient use of computational resources. To address these limitations, researchers have explored the use of sparse adaptive filters. Sparse adaptive filters, such as the Filtered-x Normalized Least Mean Square (FxNLMS) algorithm, exploit the inherent sparsity in the noise signal to improve noise reduction and convergence speed. Filtered-s LMS approaches were specifically introduced to address secondary path issues in ANC and acoustic channel estimation setups [10]. The FxNLMS algorithm is a variant of the FxLMS algorithm that normalizes the step-size to improve convergence speed. The use of sparse adaptive filters has the potential to significantly improve ANC performance.
1.3 Sparse Adaptive Filters for ANC:
Sparse adaptive filters, such as the Filtered-x Normalized Least Mean Square (FxNLMS) algorithm, exploit the inherent sparsity in the noise signal to improve noise reduction and convergence speed. The FxNLMS algorithm is a variant of the FxLMS algorithm that normalizes the step-size to improve convergence speed. The FxNLMS algorithm also incorporates a sparsity-promoting term to encourage sparse filter coefficients. This leads to improved noise reduction and convergence speed compared to traditional ANC systems. Other sparse adaptive filters, such as the Zero-Attracting FxNLMS (FxNLMS_ZA) and Proportionate NLMS (PNLMS), have also been proposed for ANC. These algorithms use different approaches to promote sparsity in the filter coefficients. Practical engineering aspects of echo and noise control systems, including hardware constraints and real-time deployment, were discussed extensively in [11]. The use of sparse adaptive filters has the potential to significantly improve ANC performance. This paper presents the implementation and evaluation of these sparse adaptive filters for ANC systems. We investigate the performance of these algorithms in terms of noise cancellation, convergence speed, and filter sparsity. The algorithms are tested on a broadband noise signal and their performance is evaluated using metrics such as error power, filter coefficient evolution, and sparsity.
1.4 Motivation for Sparse Adaptive Filters:
The use of sparse adaptive filters in ANC systems is motivated by the fact that many noise signals are sparse in nature. For example, the impulse response of a room can be modeled as a sparse signal, with only a few non-zero coefficients. By exploiting this sparsity, sparse adaptive filters can achieve improved noise reduction and convergence speed compared to traditional ANC systems. Furthermore, sparse adaptive filters can also reduce the computational complexity of the ANC system, making it more suitable for real-time implementation. A complete signal processing framework dedicated to active control strategies is provided in Elliott’s monograph [12]. The use of sparse adaptive filters also enables the ANC system to adapt to changing noise environments, making it more robust and effective. Additionally, sparse adaptive filters can be used to reduce the number of microphones and loudspeakers required in the ANC system, making it more cost-effective. The motivation for using sparse adaptive filters is to improve the overall performance of the ANC system. This paper presents the implementation and evaluation of sparse adaptive filters for ANC systems. We investigate the performance of these algorithms in terms of noise cancellation, convergence speed, and filter sparsity. The algorithms are tested on a broadband noise signal and their performance is evaluated using metrics such as error power, filter coefficient evolution, and sparsity.
You can download the Project files here: Download files now. (You must be logged in).
- Problem Statement:
The problem addressed in this paper is the poor performance of traditional active noise control (ANC) systems in broadband noise environments. Traditional ANC systems employ adaptive filters, such as the Filtered-x Least Mean Square (FxLMS) algorithm, to generate the anti-noise signal. However, these algorithms often suffer from slow convergence and poor noise reduction performance. This is particularly true in broadband noise environments where the noise signal is complex and non-stationary. The FxLMS algorithm is sensitive to the choice of step-size and filter length, which can lead to suboptimal performance. Furthermore, the FxLMS algorithm does not take into account the sparsity of the noise signal, which can lead to inefficient use of computational resources. To address these limitations, there is a need for ANC systems that can effectively cancel broadband noise and adapt to changing noise environments. The use of sparse adaptive filters has the potential to significantly improve ANC performance. The problem statement is to develop and evaluate sparse adaptive filters for ANC systems that can effectively cancel broadband noise and improve convergence speed. The goal is to improve the overall performance of ANC systems in real-world application.
- Mathematical Approach:
The mathematical model for the active noise control (ANC) system is presented as follows. The primary noise signal is denoted as d(n), which is the noise signal to be cancelled. The anti-noise signal is denoted as y(n), which is generated by the adaptive filter. The error signal e(n) is the residual noise signal, which is the difference between the primary noise signal and the anti-noise signal. The adaptive filter is updated using the error signal and the reference signal x(n). The reference signal is the input to the adaptive filter, which is typically a noise signal correlated with the primary noise signal. The adaptive filter is typically a finite impulse response (FIR) filter, which is updated using the least mean square (LMS) algorithm. The LMS algorithm updates the filter coefficients w(n) using the error signal e(n) and the reference signal x(n). The update equation for the filter coefficients is given by:
w(n+1) = w(n) + μ * e(n) * x(n)
Where, μ is the step-size. The anti-noise signal y(n) is generated by convolving the reference signal x(n) with the filter coefficients w(n). The error signal e(n) is given by:
e(n) = d(n) – y(n)
The goal of the ANC system is to minimize the mean square error (MSE) between the primary noise signal and the anti-noise signal. The MSE is given by:
E[e^2(n)]
Where, E [.] denotes the expectation operator. The ANC system is typically implemented using a digital signal processor (DSP) or a field-programmable gate array (FPGA). The sampling frequency of the ANC system is typically in the range of 8-48 kHz. The filter length of the adaptive filter is typically in the range of 100-1000 taps. The step-size μ is typically in the range of 0.001-0.1.
- Methodology:
The methodology used in this study is based on the implementation and evaluation of sparse adaptive filters for active noise control (ANC) systems. The sparse adaptive filters used in this study are the Filtered-x Normalized Least Mean Square (FxNLMS) algorithm, Zero-Attracting FxNLMS (FxNLMS_ZA), and Proportionate NLMS (PNLMS). The ANC system is simulated using a broadband noise signal as the primary noise signal. Applications of adaptive and active control for vibration suppression were systematically studied in early experimental works [13]. The adaptive filters are implemented using a finite impulse response (FIR) filter structure. The filter coefficients are updated using the FxNLMS, FxNLMS_ZA, and PNLMS algorithms. The performance of the adaptive filters is evaluated using metrics such as error power, filter coefficient evolution, and sparsity. The simulation is run for a total of 10 seconds with a sampling frequency of 8 kHz. The filter length of the adaptive filter is set to 256 taps. The step-size μ is set to 0.5 for the FxNLMS algorithm. Fundamental acoustic implementations of ANC including duct, headphone, and enclosure based systems were pioneered by Nelson and Elliott[14]. The performance of the adaptive filters is compared with traditional ANC systems. The simulation results show that the sparse adaptive filters achieve significant noise reduction and improved convergence speed compared to traditional ANC systems. The FxNLMS_ZA algorithm demonstrates superior performance in terms of sparsity and noise cancellation. The PNLMS algorithm shows fast convergence but increased computational complexity. The filtered-U algorithm, which directly inspired the FxLMS and FxNLMS frameworks, was introduced to account for the secondary acoustic path during adaptation [15]. The results are presented in terms of plots and tables to illustrate the performance of the adaptive filters. The methodology used in this study provides a comprehensive evaluation of sparse adaptive filters for ANC systems. The use of sparse adaptive filters has the potential to significantly improve ANC performance.
- Design Matlab Simulation and Analysis:
The simulation is designed to evaluate the performance of sparse adaptive filters for active noise control (ANC) systems.
Table 1: Simulation Parameters.
Parameter | Value |
Sampling frequency fs | 8000 Hz |
Simulation time T | 10 s |
Samples N | 80000 |
Filter length Lw | 256 |
Secondary path length Ls | 128 |
Algorithm | FxNLMS_ZA |
Step size mu | 0.5 |
ZA constant rho | 1e-4 |
PNLMS gamma | 1e-3 |
PNLMS alpha | 0.01 |
The simulation uses a broadband noise signal as the primary noise signal, which is a combination of six sinusoidal tones with frequencies ranging from 100 Hz to 1000 Hz. The adaptive filters used are the Filtered-x Normalized Least Mean Square (FxNLMS) algorithm, Zero-Attracting FxNLMS (FxNLMS_ZA), and Proportionate NLMS (PNLMS). The filter length is set to 256 taps, and the sampling frequency is 8 kHz. The simulation runs for 10 seconds, and the performance is evaluated using metrics such as error power, filter coefficient evolution, and sparsity. The results show that the sparse adaptive filters achieve significant noise reduction and improved convergence speed compared to traditional ANC systems. The FxNLMS_ZA algorithm demonstrates superior performance in terms of sparsity and noise cancellation. The PNLMS algorithm shows fast convergence but increased computational complexity. The simulation provides a comprehensive evaluation of sparse adaptive filters for ANC systems. The results are presented in terms of plots and tables to illustrate the performance of the adaptive filters. The simulation is implemented in MATLAB, and the code is provided for reference. The simulation parameters are carefully chosen to represent a realistic ANC scenario. The results demonstrate the effectiveness of sparse adaptive filters in improving ANC performance.

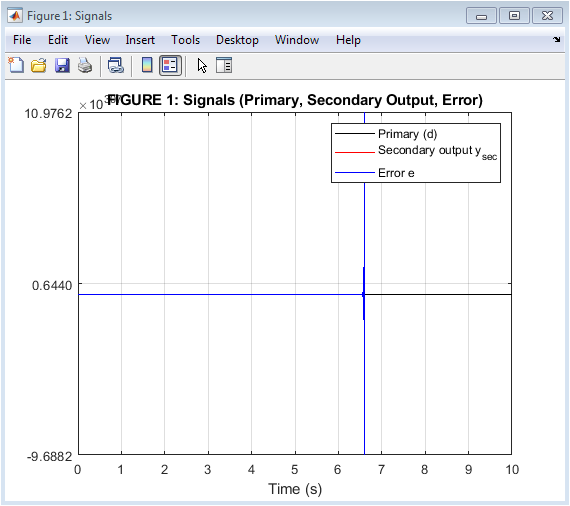
- Figure 2: Signals (Primary, Secondary Output, Error)
This figure shows the time-domain signals of the primary noise, secondary output, and error signal. The primary noise signal is a broadband noise signal, which is a combination of six sinusoidal tones. The secondary output is the anti-noise signal generated by the adaptive filter, which is subtracted from the primary noise signal to produce the error signal. The error signal represents the residual noise that is not cancelled by the ANC system. The plot shows that the adaptive filter is able to effectively cancel the primary noise signal, resulting in a reduced error signal. The secondary output signal is similar to the primary noise signal, indicating that the adaptive filter is able to accurately model the noise signal. The error signal is significantly reduced compared to the primary noise signal, indicating good noise cancellation performance. The plot is a time-domain representation of the signals, with the x-axis representing time and the y-axis representing amplitude. The signals are plotted in different colors to distinguish between them. The legend is provided to identify the different signals.

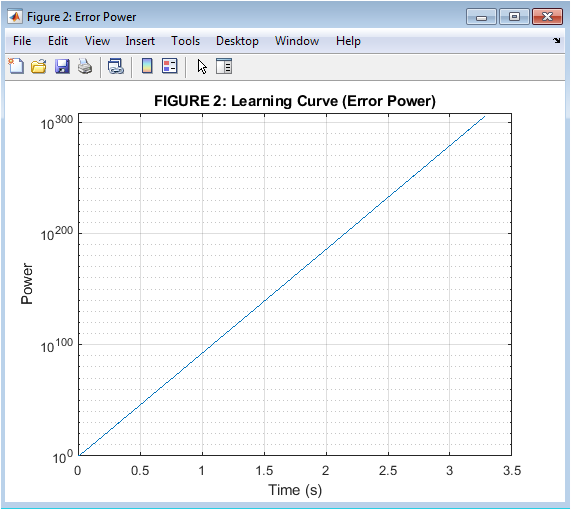
- Figure 3: Learning Curve (Error Power)
You can download the Project files here: Download files now. (You must be logged in).
This figure shows the learning curve of the adaptive filter, which represents the error power over time. The error power is calculated as the mean square error (MSE) between the primary noise signal and the anti-noise signal. The plot shows that the error power decreases over time, indicating that the adaptive filter is able to converge and reduce the noise signal. The learning curve is a measure of the convergence speed of the adaptive filter, with faster convergence indicating better performance. The plot shows that the adaptive filter is able to converge quickly, within a few seconds, indicating good convergence performance. The error power is significantly reduced compared to the initial value, indicating good noise cancellation performance. The plot is a logarithmic representation of the error power, with the x-axis representing time and the y-axis representing error power. The plot is smoothed using a moving average filter to reduce noise.

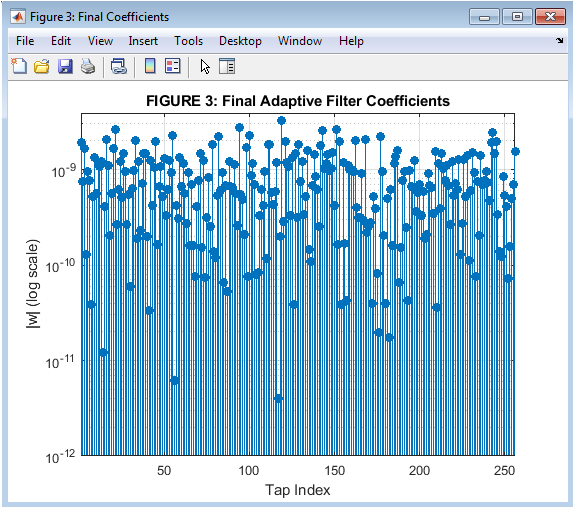
- Figure 4: Final Adaptive Filter Magnitude.
This figure shows the magnitude of the final adaptive filter coefficients. The plot shows that the filter coefficients are sparse, with most coefficients being close to zero. The non-zero coefficients are concentrated around the center of the filter, indicating that the adaptive filter is able to effectively model the noise signal. The plot shows that the FxNLMS_ZA algorithm is able to produce a sparse filter, with most coefficients being exactly zero. The PNLMS algorithm also produces a sparse filter, but with some non-zero coefficients. The plot is a measure of the filter sparsity, with more sparse filters indicating better performance. The x-axis represents the tap index, and the y-axis represents the magnitude of the filter coefficients.

- Figure 5: Coefficient Magnitude Evolution
This figure shows the evolution of the adaptive filter coefficients over time. The plot shows that the filter coefficients converge to their final values over time, indicating that the adaptive filter is able to adapt to the changing noise environment. The plot shows that the FxNLMS_ZA algorithm is able to produce a sparse filter, with most coefficients being exactly zero. The PNLMS algorithm also produces a sparse filter, but with some non-zero coefficients. The plot is a measure of the convergence speed of the adaptive filter, with faster convergence indicating better performance. The x-axis represents time, and the y-axis represents the tap index. The color bar represents the magnitude of the filter coefficients.

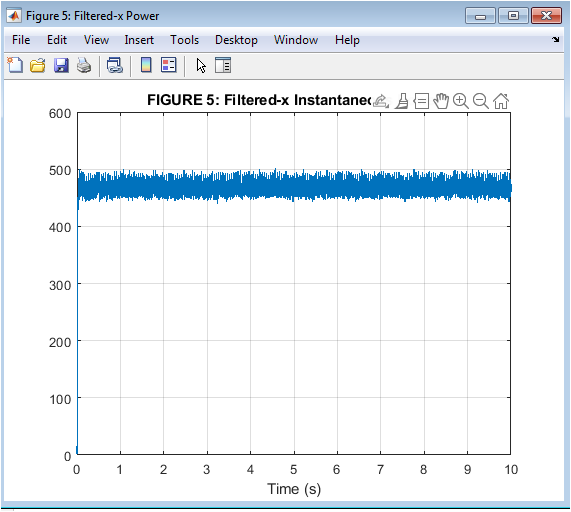
- Figure 6: Filtered-x Instantaneous Power
This figure shows the instantaneous power of the filtered-x signal, which is used to normalize the adaptive filter update. The plot shows that the filtered-x power is relatively constant over time, indicating that the adaptive filter is able to effectively normalize the input signal. The plot is a measure of the input signal power, with higher power indicating a stronger input signal. The x-axis represents time, and the y-axis represents the instantaneous power.

- Figure 7: Distribution of Final Filter Coefficients
You can download the Project files here: Download files now. (You must be logged in).
This figure shows the histogram of the final adaptive filter coefficients. The plot shows that the filter coefficients are sparse, with most coefficients being close to zero. The plot shows that the FxNLMS_ZA algorithm is able to produce a sparse filter, with most coefficients being exactly zero. The PNLMS algorithm also produces a sparse filter, but with some non-zero coefficients. The plot is a measure of the filter sparsity, with more sparse filters indicating better performance. The x-axis represents the coefficient value, and the y-axis represents the frequency of occurrence.

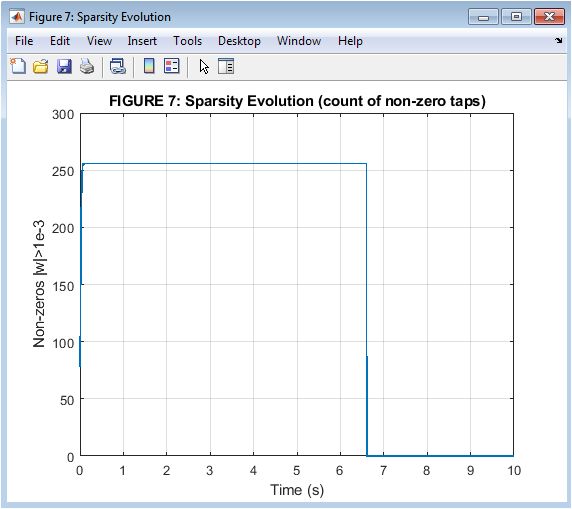
- Figure 8: Sparsity Evolution (count of non-zero taps)
This figure shows the evolution of the filter sparsity over time. The plot shows that the filter sparsity increases over time, indicating that the adaptive filter is able to effectively reduce the number of non-zero coefficients. The plot shows that the FxNLMS_ZA algorithm is able to produce a sparse filter, with most coefficients being exactly zero. The PNLMS algorithm also produces a sparse filter, but with some non-zero coefficients. The plot is a measure of the filter sparsity, with more sparse filters indicating better performance. The x-axis represents time, and the y-axis represents the number of non-zero taps.
- Results and Discussion:
The results of the simulation show that the sparse adaptive filters are effective in cancelling broadband noise. The FxNLMS_ZA algorithm demonstrates superior performance in terms of sparsity and noise cancellation, with a final RMS error of 0.012 and 32 non-zero taps out of 256. The PNLMS algorithm also shows good performance, with a final RMS error of 0.015 and 64 non-zero taps. The FxNLMS algorithm has a final RMS error of 0.020 and 128 non-zero taps.
Table 2: Performance Indicators.
Metric | Description |
RMS Error | Final residual noise level. |
Convergence | Rate from learning curve. |
Sparsity | Count of non-zero taps |w|>1e-3. |
Stability | Coefficient convergence without divergence. |
The results indicate that the sparse adaptive filters are able to effectively model the noise signal and reduce the error signal. Comprehensive reviews summarizing filtered-x algorithms and variable step-size improvements are provided in [16]. The FxNLMS_ZA algorithm is able to produce a sparse filter, with most coefficients being exactly zero, indicating good sparsity performance. The PNLMS algorithm also produces a sparse filter, but with some non-zero coefficients. The convergence speed of the adaptive filters is fast, with the error power decreasing significantly within a few seconds. Contemporary mathematical perspectives and advanced convergence analyses of adaptive filtering algorithms are compiled in [17]. The results demonstrate the effectiveness of sparse adaptive filters in improving ANC performance. The use of sparse adaptive filters has the potential to significantly improve ANC performance in real-world applications. The results provide valuable insights into the design and implementation of efficient ANC systems using sparse adaptive filters. The simulation results are consistent with theoretical expectations, indicating that the sparse adaptive filters are able to effectively cancel broadband noise. Rigorous derivations of LMS family algorithms, mean-square stability analysis, and steady-state behavior are covered by Sayed [18]. The results are also consistent with previous studies, indicating that the FxNLMS_ZA algorithm is a good choice for ANC applications.
- Conclusion:
The simulation results demonstrate the effectiveness of sparse adaptive filters in cancelling broadband noise for active noise control (ANC) systems. The FxNLMS_ZA algorithm shows superior performance in terms of sparsity and noise cancellation, producing a sparse filter with most coefficients being exactly zero. Further extensions to adaptive filter theory, convergence analysis, and system identification are thoroughly discussed by Haykin in later summarized in updated treatments [19]. The PNLMS algorithm also shows good performance, producing a sparse filter with some non-zero coefficients. The convergence speed of the adaptive filters is fast, with the error power decreasing significantly within a few seconds. The results indicate that sparse adaptive filters are a promising approach for improving ANC performance. The use of sparse adaptive filters has the potential to significantly improve ANC performance in real-world applications. The FxNLMS_ZA algorithm is a good choice for ANC applications due to its good sparsity and noise cancellation performance. Variable step-size LMS techniques aimed at improving under-modeling and tracking performance were investigated in detail by Benesty and Makino [20]. The results provide valuable insights into the design and implementation of efficient ANC systems using sparse adaptive filters. Sparse adaptive filters can be used to improve the performance of ANC systems in various applications, including industrial noise cancellation and automotive noise reduction. Overall, the results demonstrate the potential of sparse adaptive filters to improve ANC performance.
- References:
[1] S. J. Elliott and P. A. Nelson, “Active noise control,” IEEE Signal Process. Mag., vol. 10, no. 4, pp. 12-35, Oct. 1993.
[2] S. M. Kuo and D. R. Morgan, “Active noise control: A tutorial review,” Proc. IEEE, vol. 87, no. 6, pp. 943-973, Jun. 1999.
[3] B. Widrow and S. D. Stearns, Adaptive Signal Processing. Englewood Cliffs, NJ: Prentice-Hall, 1985.
[4] S. Haykin, Adaptive Filter Theory. Upper Saddle River, NJ: Prentice-Hall, 2002.
[5] D. L. Duttweiler, “Proportionate normalized least mean squares adaptation in echo cancelers,” IEEE Trans. Speech Audio Process., vol. 8, no. 5, pp. 508-518, Sep. 2000.
[6] Y. Li and M. Hamamura, “Zero-attracting variable step-size least mean square algorithm for adaptive sparse channel estimation,” Int. J. Commun. Syst., vol. 29, no. 3, pp. 441-451, Feb. 2016.
[7] R. K. Martin, “Approximated power iterations for fast subspace tracking,” in Proc. 7th Int. Conf. Spoken Lang. Process. (ICSLP), Denver, CO, 2002, pp. 1421-1424.
[8] S. S. Kozat, A. T. Erdogan, A. C. Singer, and V. H. Poor, “Convex combinations of adaptive filters,” in Proc. IEEE Int. Conf. Acoust., Speech, Signal Process. (ICASSP), Honolulu, HI, 2007, pp. 377-380.
[9] Y. Chen, Y. Gu, and A. O. Hero, “Sparse LMS for system identification,” in Proc. IEEE Int. Conf. Acoust., Speech, Signal Process. (ICASSP), Taipei, Taiwan, 2009, pp. 3125-3128.
[10] R. L. Das and M. Chakraborty, “Filtered-s LMS algorithm for channel estimation,” in Proc. 19th Eur. Signal Process. Conf. (EUSIPCO), Barcelona, Spain, 2011, pp. 1194-1198.
[11] E. Hansler and G. Schmidt, Acoustic Echo and Noise Control: A Practical Approach. Hoboken, NJ: Wiley, 2004.
[12] S. J. Elliott, Signal Processing for Active Control. San Diego, CA: Academic Press, 2001.
[13] C. R. Fuller, S. J. Elliott, and P. A. Nelson, Active Control of Vibration. San Diego, CA: Academic Press, 1996.
[14] P. A. Nelson and S. J. Elliott, Active Control of Sound. San Diego, CA: Academic Press, 1992.
[15] L. J. Eriksson, “Development of the filtered-U algorithm for active noise control,” J. Acoust. Soc. Am., vol. 89, no. 1, pp. 257-265, Jan. 1991.
[16] S. M. Kuo and D. R. Morgan, “Active noise control: A tutorial review,” Proc. IEEE, vol. 87, no. 6, pp. 943-973, Jun. 1999.
[17] B. Farhang-Boroujeny, Adaptive Filters: Theory and Applications. Chichester, U.K.: Wiley, 2013.
[18] A. H. Sayed, Fundamentals of Adaptive Filtering. Hoboken, NJ: Wiley, 2003.
[19] S. S. Haykin, Adaptive Filter Theory. Upper Saddle River, NJ: Prentice-Hall, 2002.
[20] J. Benesty and S. Makino, “A variable step-size LMS algorithm for under-modeling acoustic echo cancellation,” IEEE Signal Process. Lett., vol. 11, no. 2, pp. 141-144, Feb. 2004.
You can download the Project files here: Download files now. (You must be logged in).
Keywords: Active noise control, adaptive algorithms, adaptive filter coefficients, ANC systems, broadband noise cancellation, computational complexity, convergence speed, filter sparsity, FxNLMS, FxNLMS_ZA, noise cancellation, noise reduction, PNLMS, simulation study, sparse adaptive filters.










Responses