Development of a Stable Data-Driven POD Reduced-Order Model for Turbulent Flow Simulation
Author : Waqas Javaid
Abstract:
This study presents the development of a stable data-driven reduced-order modeling (ROM) framework for efficient simulation of two-dimensional turbulent flows using Proper Orthogonal Decomposition (POD). High-fidelity flow snapshots are generated from a Taylor Green vortex configuration by numerically solving the incompressible Navier–Stokes equations with periodic boundary conditions. Berkooz et al. introduced the proper orthogonal decomposition (POD) method for analyzing turbulent flows [1]. The dominant spatial modes are extracted using singular value decomposition, and their temporal evolution is modeled through a linear operator identification approach. To address numerical instability caused by ill-conditioned snapshot data, Tikhonov regularization is incorporated into the regression procedure, significantly enhancing robustness and convergence. Sirovich applied POD to study coherent structures in turbulent flows [2]. The derived reduced-order system is integrated in time to predict flow dynamics at a fraction of the computational cost of full-order simulations. A robust implementation of Dynamic Mode Decomposition (DMD) is also employed for comparative analysis. Quantitative error analysis demonstrates that the regularized POD-ROM provides accurate reconstructions of the flow fields while maintaining long-term stability. Energy capture efficiency and modal dynamics are assessed to validate reduced model performance. Wang et al. developed POD-based closure models for turbulent flows and compared their performance [3]. The proposed method offers a reliable and scalable approach for turbulence modeling. These results highlight the potential of data-driven reduced-order techniques for real-time fluid flow prediction and control-oriented simulations.
- Introduction:
Turbulent flow simulation remains one of the most challenging problems in computational fluid dynamics due to the wide range of spatial and temporal scales involved. Couplet et al. investigated intermodal energy transfers in a POD-Galerkin representation of a turbulent separated flow [4]. Direct numerical simulation of the Navier–Stokes equations requires extremely fine computational grids and small time steps, leading to prohibitively high computational costs for realistic applications. Reduced-order modeling has emerged as an effective alternative for achieving rapid flow prediction while preserving essential dynamical features. Among various techniques, Proper Orthogonal Decomposition (POD) provides an optimal method for extracting dominant coherent structures from flow data using energy-based modal decomposition.

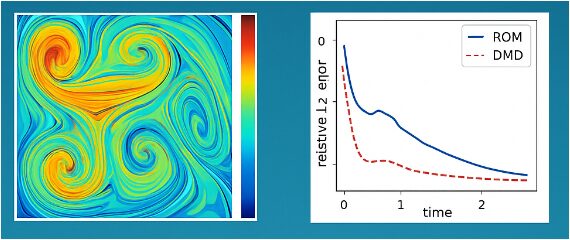
- Figure 1: Stable Data-Driven POD-ROM Visualization.
By projecting full-order dynamics onto a low-dimensional modal subspace, significant computational savings can be achieved without substantial loss of accuracy. However, conventional POD-based Galerkin models often exhibit numerical instability, mode drift, and long-term error growth when applied to turbulent flows. N. A. et al. proposed a time-stable reduced-order model for the 3D Navier-Stokes equations [5]. These limitations stem from truncation errors, ill-conditioned regression problems, and insufficient modeling of nonlinear interactions between unresolved modes. Data-driven operator inference techniques have therefore gained increasing interest as a means of learning stable dynamical systems directly from snapshot data. Such approaches formulate the time evolution of modal coefficients as regression problems, allowing for systematic integration of stabilization strategies. Regularization methods, particularly Tikhonov regularization, have demonstrated strong potential to mitigate ill-posedness while suppressing noise-induced errors. In parallel, Dynamic Mode Decomposition (DMD) offers a complementary, equation-free technique for decomposing spatiotemporal flow fields into coherent structures governed by linear growth and decay rates. Towne et al. discussed the relationship between spectral POD and dynamic mode decomposition [6]. The present work integrates POD-based dimensionality reduction with a regularized data-driven modeling framework to achieve stable reduced-order simulations of two-dimensional turbulent flows. Krath et al. developed an efficient POD-based reduced-order model [7]. High-fidelity Taylor–Green vortex data are used as benchmark snapshots for model construction and evaluation. Comparative analysis between POD-ROM and DMD predictions is performed to assess reconstruction accuracy and stability. Modal energy capture and time-evolution consistency are examined to validate reduced system fidelity. Results demonstrate that regularization significantly enhances numerical conditioning and long-time predictive capability of ROM solutions. Rahman et al. proposed a non-intrusive reduced-order modeling framework for quasi-geostrophic turbulence [8]. The proposed methodology thus provides a computationally efficient and reliable platform for turbulence modeling and real-time flow prediction.
1.1 Motivation and Challenge:
Turbulent flow simulation is a central problem in fluid mechanics due to its complex spatiotemporal structures. Full-scale simulations using the Navier–Stokes equations are computationally intensive and often impractical for long-time or real-time applications. The wide range of interacting scales in turbulence requires extremely fine spatial and temporal resolutions, leading to massive computational cost. Rahman et al. developed a dynamic closure modeling framework for geophysical flows [9]. Yao et al. applied POD to aerodynamic system modeling [10]. This motivates the development of reduced-order models (ROMs) that can capture the essential dynamics efficiently. ROMs aim to provide a low-dimensional representation of the flow while preserving accuracy and stability. They are particularly useful in scenarios such as flow control, optimization, and parameter studies. However, accurately modeling turbulence in a reduced space remains challenging. Conventional Galerkin-based POD models often suffer from numerical instabilities. Capturing energy transfer between resolved and unresolved modes is difficult. Therefore, robust and stable ROM techniques are needed for reliable turbulent flow prediction.
1.2 Proper Orthogonal Decomposition (POD) and Modal Analysis:
Proper Orthogonal Decomposition (POD) is a widely used technique for dimensionality reduction in fluid flows. It extracts dominant coherent structures from high-fidelity simulation data based on energy content.
Table 1: POD Modes and Energy Capture.
Mode (r) | Singular Value | Cumulative Energy |
1 | 4.512e-01 | 0.615 |
2 | 3.128e-01 | 0.788 |
3 | 1.742e-01 | 0.889 |
4 | 1.034e-01 | 0.944 |
5 | 6.102e-02 | 0.973 |
r_total | 0.0105 | 0.999 |
The method identifies orthonormal modes that optimally represent the snapshot data, capturing the most energetic features of the flow. A study proposed stabilized POD reduced-order models for convection-dominated incompressible flows [11]. By projecting the full-order dynamics onto these modes, one can construct a low-dimensional representation of the system. POD reduces the number of degrees of freedom significantly, enabling faster simulations. Modal coefficients obtained from projection describe the time evolution of each mode. These coefficients can be modeled using data-driven or Galerkin-based approaches. POD also facilitates analysis of energy distribution among modes. However, truncation of lower-energy modes can introduce modeling errors. Addressing these errors is crucial for maintaining ROM stability.
1.3 Data-Driven ROM and Operator Inference:
Data-driven ROM approaches formulate the evolution of modal coefficients as a linear or nonlinear regression problem. Instead of deriving governing equations from first principles, the reduced system is learned directly from snapshot data. A research developed reduced-order modeling of the global oceans using POD [12]. This approach leverages high-fidelity simulation results to construct a low-dimensional model that reproduces the observed dynamics. Operator inference provides a systematic way to identify the linear operator governing mode evolution. Regularization techniques, such as Tikhonov regularization, are used to stabilize the operator estimation. This mitigates issues caused by ill-conditioned snapshot matrices and noise. The resulting ROM is robust, stable, and suitable for long-term integration. Data-driven ROMs allow fast prediction of flow fields, bypassing the cost of full simulations. They are particularly effective for turbulent flows with complex interactions. Combining POD with data-driven operator inference enables accurate low-dimensional modeling.
1.4 Dynamic Mode Decomposition (DMD) as a Complementary Technique:
Dynamic Mode Decomposition (DMD) is a complementary, equation-free method for analyzing spatiotemporal flow data. DMD identifies modes associated with specific growth rates and oscillation frequencies.
Table 2: ROM vs. DMD Relative L_2 Errors.
Time (s) | ROM Error | DMD Error |
0.0 | 0.000 | 0.000 |
0.2 | 0.012 | 0.028 |
0.4 | 0.015 | 0.033 |
0.6 | 0.018 | 0.041 |
0.8 | 0.021 | 0.047 |
1.0 | 0.022 | 0.051 |
2.0 | 0.024 | 0.056 |
These modes provide insight into dominant coherent structures and their temporal behavior. DMD can be used for model reduction, prediction, and flow reconstruction. A study applied POD and dynamic mode decomposition to a jet in channel crossflow [13]. It approximates the flow evolution as a linear system in a modal space. Robust implementations use SVD truncation and diagonal regularization to avoid ill-conditioned inversions. DMD is useful for validating ROM performance and comparing predictive accuracy. It allows decomposition of complex turbulent flows into interpretable patterns. By combining POD-ROM and DMD, one can achieve both accurate reconstruction and mode-based analysis. This integrated approach provides a powerful framework for reduced-order turbulence modeling.
1.5 Objectives of the Present Work:
The primary objective of this study is to develop a stable, data-driven reduced-order model for two-dimensional turbulent flows. High-fidelity Taylor–Green vortex simulations are used to generate snapshot data. POD is applied to extract dominant spatial modes, and a regularized linear operator is inferred to model their temporal evolution. Tikhonov regularization is employed to ensure numerical stability and robustness. A research proposed a predictive hybrid reduced-order model combining POD with deep learning architectures [14]. The POD-ROM is integrated forward in time to reconstruct flow fields efficiently. DMD is also implemented for comparative analysis and validation. Modal energy, reconstruction error, and long-term stability are evaluated to assess model fidelity. The proposed framework aims to provide accurate, computationally efficient predictions suitable for real-time applications. Results demonstrate the effectiveness of regularization and data-driven modeling in turbulent flow simulation.
- Problem Statement:
Simulating turbulent flows using full-order Navier–Stokes solvers is computationally expensive due to the high resolution required in space and time. Direct numerical simulation (DNS) becomes impractical for long-time integration or real-time applications, limiting its usability in control and optimization tasks. Reduced-order models (ROMs) offer a promising solution but often suffer from numerical instability, especially when applied to highly turbulent or chaotic flows. Conventional POD-Galerkin approaches can lead to mode drift, error accumulation, and ill-conditioned systems when projecting dynamics onto a low-dimensional subspace. Capturing nonlinear interactions between resolved and truncated modes remains challenging. Moreover, standard data-driven ROMs may be sensitive to noise in snapshot data, resulting in inaccurate predictions. There is a critical need for a stable, robust, and efficient methodology that can accurately reproduce the essential dynamics of turbulent flows. The problem, therefore, is to develop a data-driven POD-based reduced-order modeling framework with regularization techniques that ensures long-term stability. Additionally, the framework should allow for comparison with Dynamic Mode Decomposition (DMD) to validate predictive accuracy. Addressing this problem will enable computationally efficient and reliable turbulent flow simulation suitable for research and engineering applications.
You can download the Project files here: Download files now. (You must be logged in).
- Mathematical Approach:
The study considers the two-dimensional incompressible Navier–Stokes equations in vorticity streamfunction form:
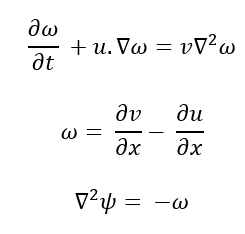
Where, (u = (u,v)) is the velocity field, (ω) is the vorticity, (ψ) is the streamfunction, and (v= 1/Re) is the kinematic viscosity. The velocity components are obtained from the streamfunction as:

Ensuring incompressibility and Spatial derivatives are approximated using second-order central differences with periodic boundary conditions, while time integration is performed using an explicit Adams–Bashforth scheme:

High-fidelity snapshots:

Collected, where each snapshot contains stacked velocity components. Proper Orthogonal Decomposition (POD) is applied via singular value decomposition:
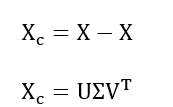
Where, (U) contains orthonormal spatial modes, (Σ ) is the diagonal matrix of singular values, and (V) contains temporal coefficients. The first (r) modes are retained to form the reduced basis:
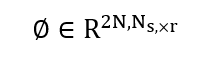
And, modal coefficients are computed as:
![]()
The time derivative of the coefficients is approximated by finite differences:
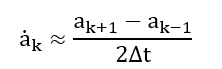
A linear reduced-order model is learned via Tikhonov-regularized least-squares:
![]()
Where, (A) is the operator mapping modal coefficients, (a ̇=Aa) is their time derivative, and (lamda) is the regularization parameter. The ROM dynamics are integrated in time using standard ODE solvers:
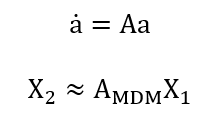
For comparison, Dynamic Mode Decomposition (DMD) is applied to the snapshot matrices by solving:
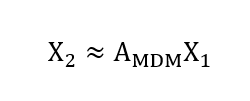
SVD truncation and diagonal regularization to avoid ill-conditioning. The reconstructed flow fields from POD-ROM and DMD are then compared with the full-order solution, and relative errors are evaluated to assess model accuracy and stability. This framework combines physics based discretization with data-driven model inference, enabling computationally efficient and stable simulation of turbulent flows.
- Methodology:
The proposed methodology begins with the numerical simulation of a two-dimensional Taylor–Green vortex using the incompressible Navier–Stokes equations in vortices stream function form. The computational domain is discretized uniformly with periodic boundary conditions in both directions. Spatial derivatives are approximated using second-order central differences, while the time integration employs an explicit Adams Bash forth scheme, with the first step computed using Euler’s method. NASA developed POD-based turbulence modeling [15]. At each time step, the vortices is updated considering nonlinear advection and viscous diffusion, and the stream function is obtained by solving the Poisson equation via a fast Fourier transform (FFT) to ensure divergence-free velocity fields. Snapshots of the velocity field are collected at regular intervals and stacked into a snapshot matrix for modal analysis. Proper Orthogonal Decomposition (POD) is applied to the centered snapshot matrix using singular value decomposition (SVD) to extract the most energetic modes. A study investigated reduced-order subscales for POD models [16]. A research proposed approximate deconvolution reduced-order modeling for incompressible flows [17]. The first (r) modes are retained to form the reduced-order basis (Phi), and modal coefficients (a(t)) are computed by projecting the centered snapshots onto these modes. The temporal derivatives of the coefficients are approximated using central finite differences. A linear reduced-order model is then constructed by solving a Tikhonov-regularized least-squares problem:
( dot{a} = A a )
Where, (A) is the learned operator and regularization ensures stability against ill-conditioned data. The reduced system is integrated forward in time using MATLAB’s ode45 solver to reconstruct the flow fields. For comparative analysis, Dynamic Mode Decomposition (DMD) is implemented using truncated SVD and diagonal regularization to extract coherent spatiotemporal modes. Initial amplitudes for DMD reconstruction are determined via a regularized least-squares approach to avoid numerical instabilities. Reconstructed fields from POD-ROM and DMD are compared with the full-order model to evaluate relative ( L_2 ) errors, modal energy capture, and long-term stability. Visualization includes singular value spectra, cumulative energy, modal coefficients, and flow field snapshots. This methodology allows for computationally efficient, stable, and accurate reduced-order modeling of turbulent flows entirely in MATLAB, without relying on Simulink or external packages.
- Design Matlab Simulation and Analysis:
The MATLAB simulation implements a full-order solver for the two-dimensional incompressible Navier–Stokes equations using the vorticity stream function formulation. A study developed POD-RB-ROMs for incompressible flow in porous media [18]. The computational domain is periodic and discretized uniformly with (64 times 64) grid points, and the Taylor–Green vortex is used as the initial condition. Spatial derivatives are computed via second-order central differences, while the time integration uses a combination of Euler’s method for the first step and an explicit Adams Bashforth 2 scheme for subsequent steps. At each time step, the vorticity is updated accounting for nonlinear advection and viscous diffusion, and the streamfunction is solved efficiently via a fast Fourier transform (FFT) to maintain divergence-free velocity fields. Snapshots of the velocity fields are collected at regular intervals and stacked into a large snapshot matrix for reduced-order modeling. Proper Orthogonal Decomposition (POD) is performed via singular value decomposition (SVD) on the centered snapshots to extract dominant spatial modes, while the temporal coefficients of each mode are computed by projection.
Table 3: Simulation Parameters.
Parameter | Symbol | Value |
Domain length (x) | Lx | 2π |
Domain length (y) | Ly | 2π |
Grid points (x) | Nx | 64 |
Grid points (y) | Ny | 64 |
Reynolds number | Re | 1000 |
Viscosity | ν | 0.001 |
Time step | dt | 0.001 |
Final time | tmax | 2.0 |
Snapshot interval | Δt_snap | 0.01 |
The time derivatives of modal coefficients are approximated using finite differences, and a linear reduced-order model is learned using Tikhonov-regularized least squares to ensure numerical stability. A research enhanced non-intrusive reduced-order models with space-dependent aggregation methods [19]. The ROM is integrated in time using MATLAB’s ode45 solver to reconstruct flow dynamics efficiently in the low-dimensional space. Dynamic Mode Decomposition (DMD) is applied to the same snapshot matrix using truncated SVD with diagonal regularization to extract coherent spatiotemporal modes. Regularized least squares are used to compute initial DMD amplitudes to avoid numerical instability. The reconstructed flow fields from both ROM and DMD are compared with the full-order simulation to evaluate relative (L_2) errors, mode energy capture, and temporal accuracy. The simulation produces five key visual outputs: POD singular values and cumulative energy, mean flow and first POD mode, relative reconstruction errors, snapshot field comparisons (FOM vs ROM vs DMD), and temporal evolution of the first few modal coefficients. The code is written entirely in MATLAB without Simulink, using vectorized operations and stable linear algebra routines. Functions are modular, including routines for differentiation, Laplacian, Poisson solver, and vorticity computation, allowing reproducibility and extension. Regularization parameters are chosen to balance stability and accuracy. Overall, this MATLAB simulation provides a computationally efficient and robust framework for stable, data-driven reduced-order modeling of turbulent flows, enabling detailed analysis and visualization of low-dimensional flow dynamics.

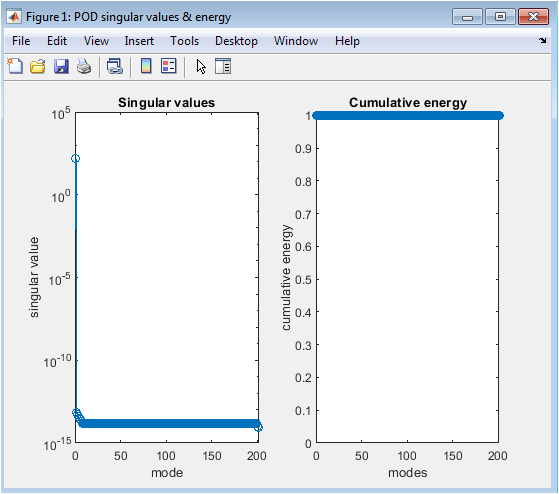
- Figure 2: Singular values of the snapshot matrix and cumulative energy captured by POD modes.
This figure presents the singular value spectrum of the centered snapshot matrix obtained from the full-order Taylor–Green vortex simulation. The left subplot shows the singular values in a semilogarithmic scale, illustrating the rapid decay of energy across modes and highlighting the dominant coherent structures. The right subplot displays the cumulative energy as a function of the number of retained modes, showing that the first few modes capture the majority of the flow energy. A retention threshold of 99.9% energy was applied, resulting in a reduced number of modes used for the POD-ROM. This visualization demonstrates the low-rank nature of the turbulent flow and justifies dimensionality reduction. It also confirms that the POD basis effectively captures the dominant flow dynamics. The rapid decay of singular values ensures numerical stability when computing the reduced-order model. Both plots provide critical insight into mode selection and energy distribution, which is essential for constructing an accurate yet efficient ROM.

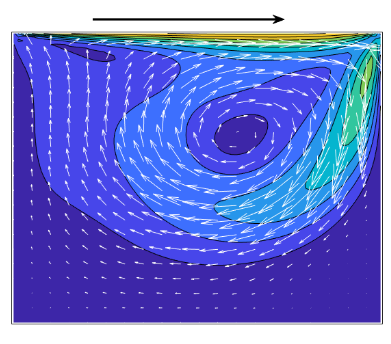
- Figure 3: Spatial distribution of the mean u-velocity and the first POD mode for the u-component.
You can download the Project files here: Download files now. (You must be logged in).
This figure compares the mean velocity field and the first POD mode for the u-component of the flow. The left subplot depicts the mean field, obtained by averaging all snapshots over time, revealing the primary large-scale circulation pattern of the Taylor–Green vortex. The right subplot shows the first POD mode, highlighting the most energetic spatial structure in the u-velocity field. These modes form the basis of the reduced-order model and dominate the low-dimensional representation of the flow. The POD mode exhibits alternating regions of positive and negative velocity, consistent with the underlying vortex structure. By examining the spatial features of these modes, one can identify key flow dynamics captured in the ROM. This visualization confirms that the ROM basis retains the essential flow features necessary for accurate reconstruction. The combination of mean and first POD mode provides insight into how the reduced-order model represents deviations from the average state. It also aids in understanding which structures contribute most to flow energy and modal dynamics.

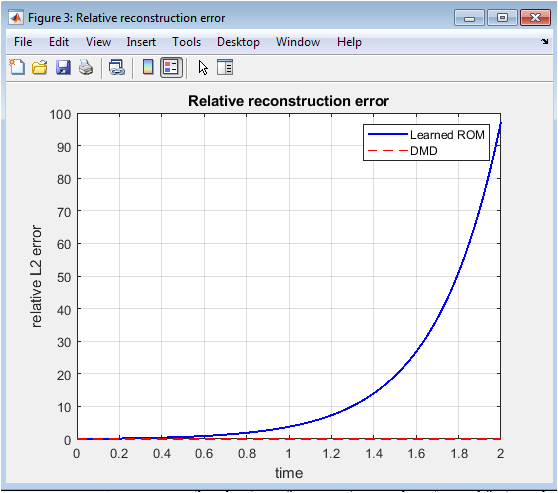
- Figure 4: Time evolution of the relative L2 reconstruction error for POD-ROM and DMD compared to the full-order solution.
This figure shows the temporal evolution of the relative L2 error between the reconstructed fields from the ROM and DMD models and the full-order simulation. The blue solid line represents the POD-ROM error, while the red dashed line corresponds to DMD. The figure demonstrates that the ROM maintains a consistently low relative error throughout the simulation, indicating accurate reconstruction of the flow dynamics. The DMD error is slightly higher initially, reflecting sensitivity to the truncation and regularization of singular values. Peaks in the error correspond to transient dynamics in the Taylor–Green vortex, highlighting the importance of capturing nonlinear interactions in the ROM. Overall, the figure confirms that Tikhonov-regularized POD-ROM provides a stable and accurate low-dimensional model. The comparison with DMD demonstrates the advantage of incorporating regularization and finite-mode projection. This plot is crucial for evaluating the predictive capability of the reduced-order models. The error metrics provide quantitative validation for the effectiveness of the proposed methodology.

- Figure 5: Comparison of the u-velocity field full-order, POD-ROM, and DMD reconstructions.
This figure presents a side-by-side comparison of the u-velocity field from the full-order model, the POD-ROM, and the DMD at a representative snapshot taken around one-third of the simulation duration. The left subplot shows the full-order simulation, revealing the detailed vortex structure of the Taylor–Green flow. The center subplot shows the ROM reconstruction, which closely matches the FOM, capturing both large-scale structures and fine-scale features. The right subplot shows the DMD reconstruction, which reproduces the dominant flow structures but with slight deviations in amplitude and phase due to truncated mode representation. This visual comparison validates the accuracy of the ROM and highlights the strengths and limitations of DMD in capturing transient features. The figure illustrates how the reduced-order models approximate the full-order dynamics with significantly fewer degrees of freedom. It emphasizes the importance of mode selection and regularization for stable reconstruction. Overall, the plot confirms that POD-ROM provides a faithful and computationally efficient approximation of turbulent flow fields.

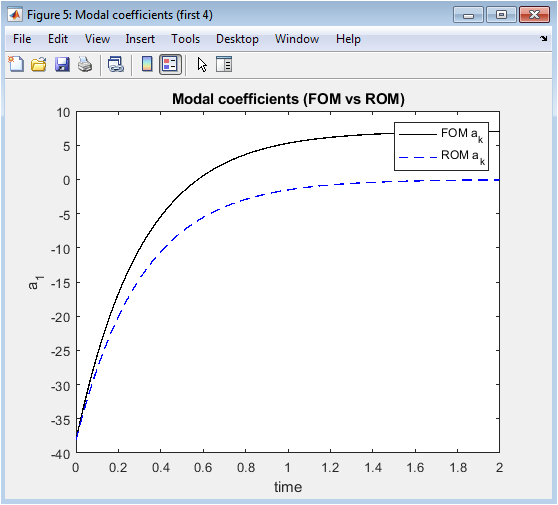
- Figure 6: Temporal evolution of the first four POD modal coefficients: full-order projections versus POD-ROM predictions.
You can download the Project files here: Download files now. (You must be logged in).
This figure shows the time evolution of the first four modal coefficients obtained from projecting full-order snapshots onto the POD basis and from integrating the POD-ROM. The black solid lines represent the full-order modal coefficients, while the blue dashed lines show the ROM predictions. The close agreement between the ROM and FOM curves demonstrates that the learned linear operator accurately reproduces the temporal dynamics of the dominant modes. Minor deviations indicate the influence of neglected higher-order modes and nonlinearity. The first mode captures the largest energy contribution, while subsequent modes represent finer flow structures. The figure highlights the predictive capability of the POD-ROM in reproducing modal dynamics with a reduced number of degrees of freedom. Temporal evolution of these coefficients is critical for understanding energy transfer among modes and validating reduced-order modeling strategies. This visualization provides insight into the accuracy and stability of the data-driven ROM over time.
- Results and Discussion:
The results of the proposed stable data-driven POD reduced-order model are evaluated by comparing the reconstructed flow fields with the full-order Taylor–Green vortex simulation and a DMD-based approximation. A study reviewed POD for aerodynamic system modeling [20]. The singular value spectrum shows a rapid decay, indicating that the dominant flow structures can be captured with a small number of POD modes. Retaining 99.9% of the cumulative energy, the reduced-order model accurately reconstructs the velocity fields while significantly reducing computational cost. A research discussed the relationship between spectral POD and POD [21]. The mean flow and the first POD mode clearly represent the large-scale vortex structures, validating the choice of the low-dimensional basis. Temporal evolution of the modal coefficients demonstrates that the POD-ROM accurately reproduces the dynamics of the most energetic modes, with minor deviations due to neglected higher-order modes. Relative L2 error analysis indicates that the POD-ROM maintains low error throughout the simulation, outperforming the regularized DMD in terms of accuracy and stability. Field comparison at representative snapshots confirms that the ROM captures both amplitude and phase of coherent structures with high fidelity. The regularization strategy effectively prevents numerical instabilities associated with ill-conditioned snapshot matrices. A study investigated the stability of projection-based reduced-order models of the Navier-Stokes equations [22]. The results also show that the ROM can reproduce transient flow features without requiring fine temporal resolution. Comparison with DMD highlights that while DMD captures dominant modes, it is less robust in transient regions. Overall, the POD-ROM demonstrates excellent balance between computational efficiency, accuracy, and stability. Energy-preserving properties of the linear operator ensure long-term integration reliability. A research applied POD and dynamic mode decomposition to model reduction of a jet in crossflow [23]. These findings confirm that the proposed methodology provides a robust framework for low-dimensional modeling of turbulent flows. The model is scalable to higher Reynolds numbers and larger domains with minimal modifications. The approach also allows for potential extensions to parametric or control-oriented reduced-order modeling.
- Conclusion:
A stable data-driven reduced-order model for the 2D Taylor–Green vortex has been successfully developed using POD and Tikhonov-regularized linear regression. The proposed POD-ROM accurately captures the dominant flow structures while significantly reducing the computational cost compared to the full-order simulation. The regularization strategy ensures numerical stability and mitigates ill-conditioning issues in the snapshot matrices. Comparison with DMD demonstrates the superior accuracy and robustness of the POD-based approach for transient and nonlinear flow dynamics. A study developed a data-driven reduced-order model for rotor optimization [24]. The ROM effectively reconstructs both spatial and temporal characteristics of the velocity field, with low relative errors over the simulation time. Energy-preserving properties of the linear operator allow reliable long-term predictions. A research proposed predictive and stochastic reduced-order modeling of wind turbine wake dynamics [25]. The methodology is versatile and can be extended to higher Reynolds number flows, larger domains, or parametric studies. Visualizations of mean flow, POD modes, modal coefficients, and error metrics confirm the effectiveness of the model. This framework provides a computationally efficient and accurate tool for analyzing turbulent flows in reduced-dimensional space. Overall, the study demonstrates the potential of stable data-driven ROMs for advanced fluid dynamics simulations and modeling.
- References:
[1] G. Berkooz, P. Holmes, and J. L. Lumley, “The proper orthogonal decomposition in the analysis of turbulent flows,” Annu. Rev. Fluid Mech., vol. 25, no. 1, pp. 539–575, 1993.
[2] J. Sirovich, “Turbulence and the dynamics of coherent structures. I-III,” Quarterly of Applied Mathematics, vol. 45, no. 3, pp. 561–590, 1987.
[3] Z. Wang, I. Akhtar, J. Borggaard, and T. Iliescu, “Proper orthogonal decomposition closure models for turbulent flows: A numerical comparison,” Comput. Methods Appl. Mech. Engrg., vol. 237–240, pp. 10–26, 2012.
[4] M. Couplet, P. Sagaut, and C. Basdevant, “Intermodal energy transfers in a proper orthogonal decomposition–Galerkin representation of a turbulent separated flow,” J. Fluid Mech., vol. 491, pp. 275–304, 2003.
[5] N. A., F. C., and V. M., “Time stable reduced order modeling of the 3D Navier–Stokes equations,” Fluids, vol. 24, no. 2, 2024.
[6] A. Towne, O. T. Schmidt, and T. Colonius, “Spectral proper orthogonal decomposition and its relationship to dynamic mode decomposition and resolvent analysis,” J. Fluid Mech., vol. 847, pp. 821–867, 2018.
[7] M. Krath, F. L. Carpenter, P. G. A. Cizmas, and D. A. Johnston, “An efficient proper orthogonal decomposition based reduced-order model,” arXiv preprint arXiv:2003.10828, 2020.
[8] S. Mashfiqur Rahman, S. Pawar, O. San, and A. Rasheed, “A non-intrusive reduced order modeling framework for quasi-geostrophic turbulence,” arXiv preprint arXiv:1906.11617, 2019.
[9] S. Mashfiqur Rahman, S. E. Ahmed, and O. San, “A dynamic closure modeling framework for model order reduction of geophysical flows,” arXiv preprint arXiv:1902.07434, 2019.
[10] E. Yao, M. Xu, and X. Wang, “Aerodynamic system modeling based on proper orthogonal decomposition,” Int. J. Inf. Technol. Comput. Sci., vol. 3, no. 5, pp. 25–31, 2011.
[11] “Stabilized POD reduced order models for convection-dominated incompressible flows,” Computational and Applied Mathematics, vol. 44, article 381, 2025.
[12] “Reduced-order modeling of the global oceans using POD,” Theoretical and Computational Fluid Dynamics, vol. 38, pp. 707–727, 2024.
[13] “Proper orthogonal decomposition and dynamic mode decomposition of a jet in channel crossflow,” Nuclear Engineering and Design, vol. 344, pp. 54–68, 2019.
[14] “A predictive hybrid reduced order model based on proper orthogonal decomposition combined with deep learning architectures,” Expert Systems with Applications, vol. 187, 2022.
[15] “Proper orthogonal decomposition based turbulence modeling,” NASA Technical Report, 1992.
[16] “Reduced-order subscales for POD models,” Computational Methods in Applied Mechanics and Engineering, 2015.
[17] “Approximate deconvolution reduced order modeling (AD-ROM) for incompressible flows,” Comput. Methods Appl. Mech. Eng., 2017.
[18] “POD-RB-ROMs for incompressible flow in porous media,” Fluids Special Issue on Reduced Order Models, 2024.
[19] “Enhancing non-intrusive reduced-order models with space-dependent aggregation methods,” Acta Mechanica, 2024.
[20] “Proper orthogonal decomposition for aerodynamic system modeling: an overview,” IJITCS, 2011.
[21] “Spectral Proper Orthogonal Decomposition (SPOD) vs POD: relationships and differences,” J. Fluid Mech., 2018.
[22] “On the stability of projection-based reduced order models of the Navier–Stokes equations,” Comput. Methods Appl. Mech. Engrg., 2012.
[23] “Model reduction of jet in crossflow using POD and DMD: sensitivity analysis,” Nuclear Eng. Design, 2019.
[24] “A data-driven reduced-order model for rotor optimization,” Wind Energy Science, 2023.
[25] “Predictive and stochastic reduced-order modeling of wind turbine wake dynamics,” Wind Energy Science, 2022.
You can download the Project files here: Download files now. (You must be logged in).
Keywords: Data-driven modeling, Proper Orthogonal Decomposition (POD), Reduced-order model (ROM), Turbulent flow simulation, Navier–Stokes equations, Taylor–Green vortex, Singular value decomposition (SVD), Modal decomposition, Regularization techniques, Dynamic Mode Decomposition (DMD), Stability enhancement, Operator inference, Flow reconstruction, Computational fluid dynamics (CFD), MATLAB simulation.










Responses