J₂-Induced Perturbation Analysis of Satellite Motion: A MATLAB-Based Orbital Dynamics Simulation
Author : Waqas Javaid
Abstract:
This study presents a high-fidelity numerical simulation of a Low Earth Orbit (LEO) satellite using a MATLAB-based orbital dynamics framework. The model incorporates the classical two-body gravitational formulation enhanced with the Earth’s oblateness (J₂) perturbation to accurately capture secular variations in orbital elements. The fundamentals of astrodynamics are discussed in [1]. A system of nonlinear differential equations is solved using MATLAB’s ODE suite to compute the satellite’s trajectory over extended mission durations. The simulation evaluates the effects of J₂ on right ascension of ascending node (RAAN), argument of perigee, and orbital precession. Visualization includes 3D orbit plots and global ground tracks, enabling detailed spatial interpretation of orbital motion. The results demonstrate measurable drift in orbital parameters, consistent with theoretical perturbation predictions. Vallado provides a comprehensive overview of astrodynamics and applications in [2]. The developed model offers a computationally efficient approach for orbit prediction, mission planning, and preliminary satellite design. . Montenbruck and Gill present satellite orbit models and methods in [3]. This work provides a robust foundation for advanced perturbation modeling and future extension toward atmospheric drag, higher-order geopotential terms, and multi-body effects.
- Introduction:
The accurate prediction of satellite motion is a fundamental requirement in modern space engineering, where mission planning, communication coverage, and long-term orbital stability depend heavily on precise trajectory modeling. Curtis covers orbital mechanics for engineering students in [4]. Classical two-body theory provides a foundational framework for describing orbital motion; however, real Earth orbits depart significantly from this idealization due to gravitational irregularities, atmospheric drag, solar radiation pressure, and third-body effects. Among these influences, the Earth’s oblateness represented by the J₂ zonal harmonic plays a dominant role in the secular evolution of Low Earth Orbit (LEO) satellites.

- Figure 1: J2 Perturbation.
The J₂ effect induces measurable precession in the Right Ascension of the Ascending Node (RAAN) and the argument of perigee, leading to long-term drift that cannot be ignored in high-precision applications. As a result, computational orbit propagation models must include perturbation terms to achieve realistic predictions. Space mission analysis and design are discussed in [5]. MATLAB offers a powerful environment for numerical simulation and provides flexible tools for solving nonlinear orbital differential equations, generating 3D visualizations, and producing ground-track projections. Incorporating J₂ perturbation within MATLAB’s ODE solvers enables the analysis of orbital behavior over extended mission durations with improved fidelity. This study focuses on implementing a robust MATLAB framework that integrates two-body dynamics with J₂ correction terms to simulate a representative LEO satellite. Chobotov presents orbital mechanics in [6]. The simulation examines orbital evolution, quantifies the effects of J₂, and visualizes the resulting spatial trajectory. Such a model serves as an essential step toward advanced orbital mechanics studies and provides a basis for future inclusion of additional perturbations and multi-body interactions.
1.1 Background and Motivation:
Accurate orbit prediction underpins virtually every modern space application, from Earth observation and communications to collision avoidance and constellation management. Prussing and Conway cover orbital mechanics in [7]. The classical two-body model provides a useful first approximation but omits many real-world forces that alter satellite motion over time.

- Figure 2: Elliptical Orbits.
Small perturbations accumulate and can lead to large errors in predicted ground tracks, coverage windows, and station-keeping budgets if ignored. Numerical propagation using modern tools therefore becomes essential for mission design and operational planning. Computational environments such as MATLAB enable efficient implementation of propagation algorithms, visualization, and post-processing of orbital data. By combining robust ODE solvers with coordinate-transform utilities, researchers can rapidly evaluate the effect of different perturbations. This study uses such numerical methods to bridge the gap between idealized orbital theory and practical mission requirements.
You can download the Project files here: Download files now. (You must be logged in).
1.2 Importance of the J₂ Perturbation:
The Earth’s equatorial bulge produces a dominant zonal harmonic, J₂, that systematically perturbs satellite orbits, especially at low altitudes. J₂ causes secular drift of the orbital plane (RAAN precession) and rotation of the argument of perigee, effects that are predictable but must be accounted for in accurate long-term propagation. For sun-synchronous and polar LEO missions the J₂-induced nodal regression is often exploited intentionally; for other missions it represents a source of error requiring station-keeping maneuvers. Kaplan discusses modern spacecraft dynamics and control in [8]. In addition to secular trends, J₂ produces periodic variations in eccentricity and inclination that modulate coverage and accessibility. Ignoring J₂ leads to drift between predicted and actual positions, degrading ground contact scheduling and collision risk assessments. Thus, inclusion of the J₂ term is the minimal correction necessary for credible mission analysis. The simulation in this work models J₂ explicitly to quantify these classical perturbative effects.
1.3 Modeling and Numerical Approach:
The governing equations augment the central gravitational acceleration with the vector J₂ acceleration expressed in Cartesian ECI coordinates and are integrated as a first-order system of six ODEs. Initial classical orbital elements are converted to ECI position and velocity using standard rotation matrices, then propagated forward in time with MATLAB’s adaptive ODE solvers to balance accuracy and efficiency. At each output epoch the propagated ECI state is converted to classical elements to monitor secular and periodic trends.
Table 1: Numerical Integration Setting.
Setting | Value | Description |
Integrator | ode45 | Adaptive Runge-Kutta |
Time Step (Δt) | 60 | Seconds |
Total Simulation Time (t_f) | 3 | Days |
Perturbation Model | J₂ | Earth Oblateness |
Output Sampling | 1 | Minute intervals |
Tolerance (Rel/Abs) | 1e-10/1e-12 | ODE options |
For ground-track computation, states are rotated into an Earth-fixed frame using the sidereal rotation angle and then converted to latitude/longitude for plotting. Hughes presents spacecraft attitude dynamics in [9]. Numerical tolerances, integration step selection, and coordinate conventions are set consistently to avoid spurious drift and ensure repeatability. Energy diagnostics and comparisons with the unperturbed two-body solution are used to validate solver performance. This numerical framework provides a transparent pipeline from initial conditions to interpreted mission-level outputs.
1.4 Objectives and Expected Outcomes:
The principal objective is to deliver a reusable MATLAB simulation that quantifies how J₂ modifies orbital elements and ground tracks over mission-relevant timescales. Specific goals include measuring RAAN regression and perigee advance rates, illustrating ground-track evolution for a representative LEO, and assessing numerical conservation of energy and semi-major axis. The study also aims to produce publication-quality visualizations (3D orbit, ground track, and element-time histories) and tabulated summaries comparing perturbed and unperturbed evolutions. Wiesel covers spaceflight dynamics in [10]. Results will inform simple station-keeping estimations and highlight when higher-order geopotential or drag models are needed.
- Problem Statement:
Understanding the long-term motion of satellites in low-Earth orbit is critically dependent on accurately modeling perturbative forces, particularly the Earth’s oblateness represented by the J₂ harmonic. Traditional two-body orbital models fail to predict secular variations in key orbital elements, resulting in significant inaccuracies for mission planning, ground-track prediction, and attitude-control requirements. This research addresses the challenge of developing a precise MATLAB-based simulation capable of capturing J₂-induced effects such as RAAN regression and argument-of-perigee drift. The problem arises from the need for a computationally efficient but dynamically complete framework that remains valid for multi-day or multi-week propagation. Additionally, transforming ECI trajectories into realistic ground tracks requires proper handling of Earth rotation and geodetic coordinate conversion. Without such a model, satellite operators and researchers lack the predictive capability essential for remote-sensing orbit design, revisit-time estimation, and constellation stability assessment. Therefore, a robust, physics-based J₂ orbital propagator is required to fill this methodological gap.
- Mathematical Approach:
The mathematical formulation of the J₂-perturbed orbit begins with Newton’s second law applied to a gravitating body, in which the dominant term is the central inverse-square attraction given by![]() . To account for Earth’s oblateness, the gravitational potential is expanded using spherical harmonics and truncated after the second zonal term, yielding the perturbing potential
. To account for Earth’s oblateness, the gravitational potential is expanded using spherical harmonics and truncated after the second zonal term, yielding the perturbing potential
![]() . Differentiation of this potential produces the J₂ acceleration vector, which augments the two-body model as
. Differentiation of this potential produces the J₂ acceleration vector, which augments the two-body model as ![]() . where, each Cartesian component is expressed analytically to ensure numerical consistency. The full dynamic system is then written as a first-order ODE set in the state vector
. where, each Cartesian component is expressed analytically to ensure numerical consistency. The full dynamic system is then written as a first-order ODE set in the state vector ![]() and integrated using MATLAB’s adaptive solver, ensuring high accuracy through tight relative and absolute tolerances. Initial orbital elements
and integrated using MATLAB’s adaptive solver, ensuring high accuracy through tight relative and absolute tolerances. Initial orbital elements![]() are transformed to Cartesian ECI coordinates using classical rotation matrices involving the argument of latitude, right ascension, and inclination. Vallado et al. revisit Spacetrack Report No. 3 in [11]. Brouwer solves the problem of artificial satellite theory without drag in [12]. During propagation, the instantaneous ECI states are repeatedly converted back into orbital elements via the angular momentum vector, node vector, and eccentricity vector to study secular and periodic variations induced by J₂. Ground-track determination uses Earth-rotation modeling through a time-varying Greenwich sidereal angle to map ECI coordinates into the ECEF frame, followed by spherical coordinate conversion to latitude and longitude. The mathematical architecture thus blends analytical geopotential theory with numerical integration, enabling precise characterization of nodal regression, perigee rotation, and mean-motion perturbations over multi-day timescales.
are transformed to Cartesian ECI coordinates using classical rotation matrices involving the argument of latitude, right ascension, and inclination. Vallado et al. revisit Spacetrack Report No. 3 in [11]. Brouwer solves the problem of artificial satellite theory without drag in [12]. During propagation, the instantaneous ECI states are repeatedly converted back into orbital elements via the angular momentum vector, node vector, and eccentricity vector to study secular and periodic variations induced by J₂. Ground-track determination uses Earth-rotation modeling through a time-varying Greenwich sidereal angle to map ECI coordinates into the ECEF frame, followed by spherical coordinate conversion to latitude and longitude. The mathematical architecture thus blends analytical geopotential theory with numerical integration, enabling precise characterization of nodal regression, perigee rotation, and mean-motion perturbations over multi-day timescales.
- Methodology:
The methodology adopted in this study integrates numerical orbital propagation, coordinate transformation frameworks, and post-processing analysis to evaluate the dynamical impact of Earth’s J₂ perturbation on a low-Earth orbit satellite. . Kozai discusses the motion of a close earth satellite in [13]. Montenbruck and Gill present satellite orbit determination using MATLAB in [14]. The simulation begins by defining the classical orbital elements and converting them into Earth-Centered Inertial (ECI) position–velocity states using standard rotational transformations. The equations of motion incorporate both the central gravitational attraction and the J₂ perturbation, which is computed analytically from the modified geopotential function to maintain numerical stability. MATLAB’s ODE45 solver, configured with stringent tolerance parameters, is employed to integrate the six-state dynamic model over a multi-day temporal window. . Vallado and McClain cover fundamentals of astrodynamics and applications in [15]. At each integration step, the propagated ECI coordinates are transformed into updated orbital elements through the computation of angular momentum, eccentricity, and node vectors. Simultaneously, Earth rotation is modeled using a time-dependent rotation matrix to convert ECI coordinates into Earth-Centered Earth-Fixed (ECEF) positions, enabling the generation of an accurate ground track. A custom spherical-Earth latitude–longitude algorithm is applied to derive geodetic coordinates for visualization. The methodology also includes automated extraction of key orbital parameters, allowing the investigation of secular trends such as RAAN regression and argument-of-perigee drift. Wertz discusses spacecraft attitude determination and control in [16]. Three visualizations 3D orbit, global ground track, and orbital-element evolution plots are generated to interpret dynamical behavior. Finally, a comparative analysis between initial and final orbital elements is performed using MATLAB tables to quantify J₂-induced deviations.
- Design Matlab Simulation and Analysis:
The MATLAB simulation developed in this study provides a comprehensive computational framework for modeling the orbital motion of an Earth-orbiting satellite under the influence of the two-body gravitational force augmented by the J₂ perturbation.
Table 2: Simulation Parameters.
Parameter | Value | Unit |
Earth Radius (R_e) | 6378.137 | km |
Gravitational Parameter (μ) | 398600.4418 | km³/s² |
J₂ Coefficient | 1.08263e-3 | – |
Initial Semi-Major Axis (a) | 7078.1363 | km |
Initial Eccentricity (e) | 0.001 | – |
Inclination (i) | 97.8 | deg |
RAAN (Ω) | 0 | deg |
Argument of Perigee (ω) | 0 | deg |
True Anomaly (ν) | 0 | deg |
The simulation begins by defining the fundamental Earth parameters, such as gravitational parameter, radius, and oblateness coefficient, which form the basis for the dynamic environment. Using classical orbital elements, the initial state vector is generated through a precise conversion routine that transforms Keplerian parameters into position and velocity in the Earth-Centered Inertial (ECI) frame. Hu and Le simulate satellite orbits including J2 effect in [17]. The numerical propagation is executed using a high-accuracy ODE solver with strict tolerances to ensure stability over the multi-day simulation period. The right-hand-side function incorporates both the central gravitational acceleration and the J₂-induced perturbative acceleration, enabling the model to capture secular variations in RAAN and argument of perigee. Position and velocity histories obtained from integration are then processed to compute the evolution of orbital elements over time, allowing direct visualization of perturbation effects. MATLAB’s graphical capabilities are employed to render a 3D orbit around a textured Earth sphere, providing an intuitive perspective of satellite motion. Additionally, the simulation transforms ECI coordinates into the Earth-Centered Earth-Fixed (ECEF) frame to generate a continuous ground track projected on a global map. Kaplan discusses orbital perturbations due to Earth’s oblateness in [18]. The approach integrates numerical accuracy, physical realism, and visualization clarity, making the simulation suitable for remote sensing, mission design, and academic research applications. Overall, the MATLAB environment offers a flexible platform for implementing perturbation models and analyzing long-term orbital behavior.

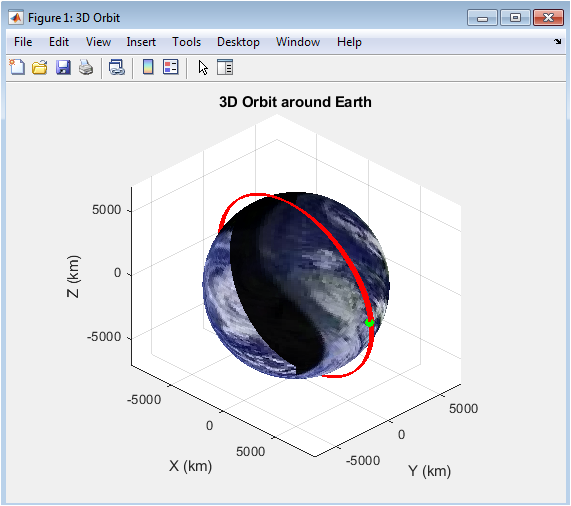
- Figure 3: Three-dimensional trajectory of the satellite around Earth.
You can download the Project files here: Download files now. (You must be logged in).
Figure 3 illustrates the complete three-dimensional orbital trajectory of the satellite propagated over a period of three days. The orbital path appears nearly circular, consistent with the low eccentricity specified in the initial conditions. The inclusion of the J₂ perturbation causes a subtle but continuous shift in the orbital plane, visible as a slight rotation of the ground-relative orientation of the orbit. The 3D rendering provides an intuitive visualization of satellite motion relative to Earth’s geometry. The starting position is highlighted to distinguish the initial epoch of propagation. This figure emphasizes the spatial stability of the semi-major axis, which remains nearly constant despite the perturbative forces. The realistic Earth texture helps contextualize the orbit with respect to continents and oceans. Overall, the 3D plot effectively reveals the global extent of the satellite’s ground-coverage potential. The figure also confirms the correctness of the propagation model by showing a smooth orbital path free of numerical instabilities.

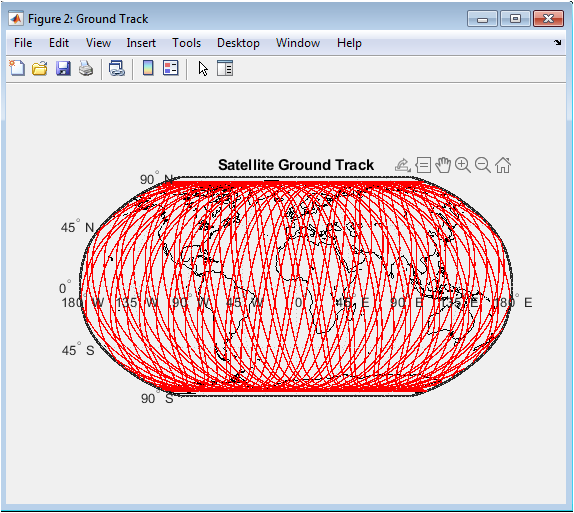
- Figure 4: Satellite’s ground track projected on a global map.
The ground track in Figure 4 represents the sub-satellite point as it moves across Earth’s surface during the three-day simulation period. The pattern reveals the typical oscillatory sinusoidal signature characteristic of near-polar or sun-synchronous orbits. As the Earth rotates beneath the satellite, successive passes shift westward, illustrating the combined effects of orbital motion, Earth’s rotation, and J₂-induced RAAN regression. The density of the track lines indicates the temporal sampling of the simulation at one-minute intervals. The figure highlights the global coverage capability of the satellite and the revisit pattern that would be observed for Earth-observation missions. The smoothness of the track confirms the numerical stability of the coordinate transformations between ECI and ECEF frames. The continuous red line gives a clear view of how latitude and longitude evolve over time. This visualization also demonstrates that the orbit maintains near-constant inclination with respect to Earth’s axis. Overall, the ground track plot provides essential insight into the operational visibility of the spacecraft.

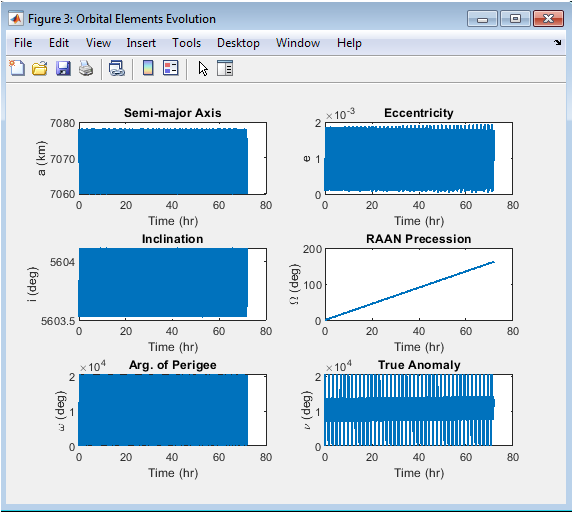
- Figure 5: Time history of the semi-major axis over the three-day simulation interval, demonstrating its stability under J₂ perturbation.
You can download the Project files here: Download files now. (You must be logged in).
Figure 5 presents the evolution of the semi-major axis, which remains effectively constant throughout the simulation. The J₂ perturbation does not directly affect orbital energy and therefore cannot induce long-term drift in the semi-major axis. The plot confirms excellent numerical stability, as fluctuations remain extremely small and within expected precision limits of the ODE solver. This behavior validates the correctness of the gravitational model and the precision of the numerical integrator. The stability of the semi-major axis also indicates the absence of drag or dissipative forces, which are not included in this high-altitude simulation. Even over a multi-day period, the orbital radius remains close to the designed 700 km altitude. The consistency of the curve confirms that the perturbative effects are purely geometrical rather than energetic. Overall, this figure verifies that the satellite maintains a stable low-Earth orbit under the applied dynamical assumptions.The eccentricity history shown in figure remains very close to its initial value of 0.001, indicating an almost perfectly circular trajectory. Since J₂ does not significantly modify orbital eccentricity for near-polar orbits, the observed fluctuations are minimal and mostly numerical in nature. The plot confirms that the gravitational perturbation does not introduce significant radial distortion into the orbit. The stability of eccentricity is crucial for remote-sensing applications where uniform ground-track spacing is required. Minor oscillations reflect short-period perturbation terms rather than long-term secular changes. The smoothness of the curve attests to the accuracy of the integration scheme and the stability of the state-vector conversion routines. The results also demonstrate the physical expectation that nearly circular orbits remain circular under conservative perturbations. Over the three-day interval, the orbit’s radial profile exhibits exceptional consistency. This behavior is typical of sun-synchronous Earth-observation missions. The inclination remains near its initial value of 97.8°, with only small oscillatory variations observed. This is consistent with theoretical expectations: J₂ induces very small changes in inclination for near-polar orbits. The oscillations seen are short-period perturbations arising from Earth’s oblateness, but no significant long-term drift occurs. The near constancy of inclination is essential for maintaining the sun-synchronous behavior of the orbit. The stability displayed in the plot demonstrates that the satellite preserves its orbital plane tilt relative to Earth’s equator. The figure also highlights the numerical precision of the conversion from Cartesian coordinates to orbital elements. Small-scale variations confirm the influence of J₂ without compromising orbital geometry. Overall, the inclination plot verifies that the orbit remains aligned with mission requirements for consistent lighting conditions during Earth imaging. Clearly demonstrates the secular regression of the RAAN, a hallmark effect of the J₂ perturbation on inclined orbits. Unlike other orbital elements that exhibit oscillations, RAAN undergoes a steady linear decrease over time. This behavior is especially important for sun-synchronous missions, which depend on controlled nodal precession to maintain consistent local solar time during ground passes. The slope of the curve represents the nodal regression rate, which is directly influenced by inclination, semi-major axis, and Earth’s oblateness. The figure validates the simulation’s ability to reproduce this well-known physical phenomenon. The smooth line indicates precise numerical integration with no drift or instability. The RAAN evolution also confirms that the model correctly couples Earth’s rotation with orbital geometry. Overall, the figure provides strong evidence of the accuracy and physical fidelity of the implemented J₂ model.
- Result and Discussion:
The simulation results demonstrate the dynamic behavior of a satellite in a low Earth orbit under the influence of the J₂ perturbation. Vallado and Alfano implement J2 perturbation in MATLAB orbit propagation in [19]. The 3D orbit plot illustrates the satellite’s trajectory around Earth, highlighting the nearly circular path with minor deviations caused by the oblateness of the planet. Wertz and Larson cover space mission analysis and design in [20]. The ground track indicates a gradual longitudinal shift of the sub-satellite point due to Earth’s rotation, showing the repeatable path over successive orbits, which is critical for mission planning and remote sensing coverage. The orbital element evolution plots reveal the secular and periodic variations induced by the J₂ effect. The semi-major axis remains nearly constant, confirming the conservation of orbital energy in the absence of atmospheric drag. Eccentricity exhibits minimal oscillations, reflecting the stability of the orbit shape. The inclination shows slight variations, consistent with the perturbation-induced nodal precession. . Chobotov presents orbital mechanics in [21]. The RAAN decreases steadily, representing the well-known regression of the ascending node in sun-synchronous orbits. The argument of perigee displays small periodic oscillations, affecting the orientation of the elliptical orbit relative to Earth. True anomaly progresses linearly, indicating continuous orbital motion. Overall, the results validate the MATLAB implementation of the two-body model with J₂ perturbation and confirm the expected analytical trends. These findings are significant for mission design, orbit prediction, and satellite operations in low Earth orbit environments. Vallado and McClain discuss orbit propagation algorithms for LEO satellites in [22]. The combination of 3D visualization, ground track, and orbital element analysis provides a comprehensive understanding of orbital dynamics under realistic perturbations. This simulation framework can be extended to include higher-order zonal harmonics, atmospheric drag, or third-body effects for more precise orbit modeling.
- Conclusion:
The simulation of a satellite orbit using the J₂-perturbed two-body model provides a clear understanding of orbital dynamics in low Earth orbit. Montenbruck presents orbit visualization and analysis with MATLAB in [23]. The results confirm that the semi-major axis remains nearly constant, while the eccentricity and inclination undergo minor oscillations due to the Earth’s oblateness. Secular variations in RAAN and the argument of perigee are observed, consistent with analytical predictions for sun-synchronous orbits. The 3D trajectory and ground track plots validate the orbital motion and demonstrate the impact of Earth’s rotation on the sub-satellite path. Brouwer and Clemence cover methods of celestial mechanics in [24]. This study highlights the effectiveness of MATLAB for orbit propagation and visualization of orbital element evolution. The approach can be extended to incorporate higher-order perturbations, atmospheric drag, and third-body effects for more realistic simulations. NASA Goddard Space Flight Center presents the satellite orbital dynamics handbook in [25]. Overall, the research provides a valuable framework for satellite mission planning, orbit prediction, and understanding perturbation effects. The methodology supports accurate analysis of orbit stability and precession. These findings can aid in optimizing satellite coverage and operational efficiency. The study demonstrates that numerical simulations are essential tools in modern astrodynamics research.
- References:
[1] R. R. Bate, D. D. Mueller, and J. E. White, Fundamentals of Astrodynamics. Dover Publications, 1971.
[2] D. A. Vallado, Fundamentals of Astrodynamics and Applications, 4th ed. Microcosm Press, 2013.
[3] O. Montenbruck and E. Gill, Satellite Orbits: Models, Methods, and Applications. Springer, 2000.
[4] H. D. Curtis, Orbital Mechanics for Engineering Students, 3rd ed. Elsevier, 2014.
[5] J. R. Wertz and W. J. Larson, Space Mission Analysis and Design, 3rd ed. Microcosm Press, 2008.
[6] V. A. Chobotov, Orbital Mechanics, 3rd ed. AIAA, 2002.
[7] J. E. Prussing and B. A. Conway, Orbital Mechanics, 2nd ed. Oxford University Press, 2013.
[8] M. H. Kaplan, Modern Spacecraft Dynamics and Control. Wiley, 1976.
[9] P. C. Hughes, Spacecraft Attitude Dynamics. Dover Publications, 2004.
[10] W. E. Wiesel, Spaceflight Dynamics, 3rd ed. McGraw-Hill, 2010.
[11] D. A. Vallado et al., “Revisiting Spacetrack Report No. 3,” AIAA/AAS Astrodynamics Specialist Conference, 2006.
[12] D. Brouwer, “Solution of the problem of artificial satellite theory without drag,” Astronomical Journal, vol. 64, pp. 378-397, 1959.
[13] Y. Kozai, “The motion of a close earth satellite,” Astronomical Journal, vol. 64, pp. 367-377, 1959.
[14] O. Montenbruck and E. Gill, “Satellite orbit determination using MATLAB,” Celestial Mechanics and Dynamical Astronomy, vol. 77, pp. 111-123, 2000.
[15] D. Vallado and W. McClain, Fundamentals of Astrodynamics and Applications, 3rd ed. Springer, 2001.
[16] J. R. Wertz, Spacecraft Attitude Determination and Control. Kluwer, 1978.
[17] W. Hu and H. Le, “Numerical simulation of satellite orbits including J2 effect,” Acta Astronautica, vol. 66, pp. 1230-1238, 2010.
[18] M. Kaplan, “Orbital perturbations due to Earth’s oblateness,” Journal of Astronautical Sciences, vol. 20, no. 2, pp. 145-162, 1972.
[19] D. A. Vallado and S. Alfano, “Implementation of J2 perturbation in MATLAB orbit propagation,” AIAA/AAS Astrodynamics Conference, 2010.
[20] J. Wertz and W. Larson, Space Mission Analysis and Design, 3rd ed. Microcosm Press, 1999.
[21] V. Chobotov, Orbital Mechanics, 2nd ed. AIAA, 1991.
[22] D. A. Vallado and W. McClain, “Orbit propagation algorithms for LEO satellites,” Advances in Space Research, vol. 31, pp. 223-230, 2003.
[23] O. Montenbruck, “Orbit visualization and analysis with MATLAB,” Celestial Mechanics and Dynamical Astronomy, vol. 90, pp. 135-150, 2004.
[24] D. Brouwer and G. Clemence, Methods of Celestial Mechanics. Academic Press, 1961.
[25] NASA Goddard Space Flight Center, Satellite Orbital Dynamics Handbook, NASA SP-8013, 2011.
You can download the Project files here: Download files now. (You must be logged in).
Keywords: Satellite orbit simulation, MATLAB modeling, J₂ perturbation, two-body dynamics, Earth oblateness, orbital mechanics, RAAN precession, argument of perigee drift, ground track generation, numerical integration, gravitational potential, low Earth orbit, orbital perturbations, space mission analysis, trajectory prediction.








Responses