Stiff Multi-Species Chemical Kinetics Simulation Using Analytical Jacobians and Sensitivity Analysis in MATLAB
Author : Waqas Javaid
Abstract:
This work presents a MATLAB-based framework for simulating stiff multi-species chemical reaction networks using advanced numerical techniques. The proposed methodology employs mass-action kinetics to model reaction rates and utilizes the stiff ODE solver `ode15s` for efficient integration across widely varying timescales. An analytical Jacobian is derived to improve solver stability and computational performance. Shampine and Reichelt developed the MATLAB ODE Suite, a collection of solvers for ordinary differential equations [1]. Reaction stoichiometry, species interdependencies, and rate constants are systematically encoded to handle complex networks. Finite-difference sensitivity analysis is implemented to quantify the influence of kinetic parameters on species concentrations. Visualization tools are incorporated to track concentration profiles, species fractions, and reaction progress. Shampine et al. presented a method for solving index-1 differential-algebraic equations (DAEs) in MATLAB and Simulink [2]. The framework ensures non-negative concentrations and accommodates zeroth- and higher-order reactions. Dense evaluation of the solution enables high-resolution plotting and post-processing. Simulation results demonstrate the method’s accuracy, stability, and robustness for stiff systems. The MathWorks provides documentation on solving stiff ODEs using MATLAB and Simulink [3]. The approach is generalizable to larger chemical networks, making it suitable for computational chemical kinetics studies.
- Introduction:
Chemical kinetics plays a pivotal role in understanding the dynamic behavior of reacting systems across chemistry, biology, and chemical engineering. Accurate modeling of multi-species reaction networks is essential for predicting species concentrations, reaction yields, and system stability. Many chemical networks exhibit stiffness due to the presence of reactions with widely varying timescales, which poses challenges for standard numerical solvers. Stiff systems require specialized integration techniques to ensure stability and efficiency.

- Figure 1: Chemical Kinetic Mechanism Simulation.
MATLAB provides a versatile platform for implementing advanced numerical methods, including stiff ODE solvers such as `ode15s`. Incorporating analytical Jacobians significantly enhances solver performance by reducing computational cost and improving convergence.
Table 1: Stoichiometric Matrix (Nu)
Species | R1 | R2 | R3 | R4 |
A | -1 | 1 | -2 | 0 |
B | -1 | 1 | 0 | -1 |
C | 1 | -1 | 0 | 0 |
D | 0 | 0 | 1 | 0 |
E | 0 | 0 | 0 | 1 |
Table 2: Reactant Stoichiometry
Species | R1 | R2 | R3 | R4 |
A | 1 | 0 | 2 | 0 |
B | 1 | 0 | 0 | 1 |
C | 0 | 1 | 0 | 0 |
D | 0 | 0 | 0 | 0 |
E | 0 | 0 | 0 | 0 |
Reaction stoichiometry and reactant dependencies are fundamental to capturing the correct system dynamics. Mass-action kinetics provides a widely accepted framework for modeling elementary reactions, enabling systematic formulation of rate equations. Sensitivity analysis is a critical tool for understanding the influence of kinetic parameters on system behavior and identifying key reactions. Postawa et al. compared various ODE solvers for biochemical problems and found significant differences in performance [4]. Finite-difference approaches offer a simple yet effective method for parameter sensitivity estimation. Visualization of species concentrations, reaction progress, and species fractions aids in interpreting complex dynamics. Ensuring non-negative concentrations is necessary for physical consistency. Aro developed CHEMSODE, a stiff ODE solver specifically designed for chemical kinetics problems [5]. The proposed MATLAB framework integrates stiff solver capabilities with analytical Jacobians, sensitivity analysis, and visualization tools. It allows efficient simulation of chemical networks with multiple interacting species. A variable step block hybrid method was proposed for solving stiff chemical kinetics problems, with comparisons to ode15s [6]. The framework is modular and can accommodate networks of varying size and complexity. High-resolution solution evaluation facilitates detailed post-processing and plotting. This approach is suitable for educational purposes, computational research, and preliminary design studies in chemical kinetics. The method is demonstrated using a representative five-species network exhibiting stiff behavior. De Florio compared new methods to MATLAB’s ode15s for solving stiff chemical kinetics problems, including ROBER and Belousov-Zhabotinskii [7]. Overall, this work provides a robust, flexible, and computationally efficient approach to simulate stiff chemical reaction systems in MATLAB.
1.1 Importance of Chemical Kinetics:
Chemical kinetics is a fundamental discipline that studies the rates and mechanisms of chemical reactions. Understanding how species interact and transform over time is crucial for fields ranging from chemistry and biochemistry to chemical engineering. It provides insights into reaction mechanisms, pathway optimization, and system stability. Kinetics governs the behavior of industrial reactors, enzymatic reactions, and atmospheric chemistry. Lecture notes summarized stiff vs nonstiff solvers and recommended ode15s for stiff problems in engineering applications [8]. Accurate modeling of reaction rates enables better control of product yields and energy efficiency. In complex systems, kinetics informs process design, safety protocols, and environmental impact assessments. Studying kinetics also allows researchers to predict transient behavior under varying conditions. Experimental data can be complemented by computational simulations to explore scenarios that are difficult to realize in the lab. Moreover, computational kinetics supports hypothesis testing and reaction mechanism verification. Therefore, chemical kinetics forms the backbone of both theoretical and applied chemical research.
1.2 Multi-Species Reaction Networks:
Many chemical and biological systems consist of multiple interacting species undergoing a network of reactions simultaneously.
Table 3: Species List.
Index | Species |
1 | A |
2 | B |
3 | C |
4 | D |
5 | E |
Modeling such multi-species networks is essential to predict concentration changes over time accurately. Each species can participate in multiple reactions, influencing the dynamics of the entire system. MIT OpenCourseWare discussed the necessity of stiff solvers in chemical and biological reaction engineering [9]. In biological pathways, metabolites interact through complex networks, while in chemical engineering, reactants and intermediates determine product distribution.

- Figure 2: Sensitivity of Chemical Species.
Multi-species networks are often nonlinear, with feedback loops that complicate analysis. Capturing all interactions ensures realistic simulations and avoids oversimplification. Computational tools are invaluable for studying these networks due to their complexity. Proper representation of stoichiometry and reaction dependencies is necessary for accurate dynamic behavior. Simulating multi-species networks allows the identification of critical reactions and species. Consequently, modeling these networks helps in optimization, control, and understanding of system behavior under various conditions.
1.3 Challenge of Stiffness:
Stiffness is a common challenge in multi-species chemical networks, arising when reactions occur at widely differing timescales. Some reactions proceed extremely fast while others evolve slowly, leading to numerical difficulties for standard ODE solvers. Stiff systems often require very small time steps to maintain stability with explicit methods, which increases computational cost. Ignoring stiffness can produce inaccurate or unstable solutions, misrepresenting system dynamics. Chemical reactions with fast equilibrium steps combined with slow overall transformations are classic examples of stiff systems. Stiffness also occurs in enzymatic networks and autocatalytic reactions. A tutorial compared the performance of explicit (ode45) and stiff (ode15s) solvers for stiff problems [10]. Proper handling of stiffness is crucial to ensure the reliability of simulation results. Computational methods designed for stiff problems can integrate fast and slow dynamics efficiently. Failure to address stiffness can result in divergence, oscillations, or negative concentrations. Recognizing stiffness is the first step toward selecting an appropriate numerical strategy.
1.4 Need for Specialized Solvers:
Specialized numerical solvers are required to handle the stiffness in chemical reaction networks efficiently. Implicit solvers, such as `ode15s` in MATLAB, are particularly suitable because they can maintain stability over large time steps.
Table 4: Solver Settings
Setting | Value |
ODE Solver | ode15s |
Absolute Tolerance | 1e-12 |
Relative Tolerance | 1e-8 |
Jacobian Provided | Yes |
These solvers reduce computational effort compared to explicit methods, which demand extremely small time steps. Ali Dinler shared a first-order stiff ordinary differential equation solver on MATLAB Central File Exchange [11]. The use of stiff solvers ensures accurate capture of both fast and slow dynamics without sacrificing performance. They are especially important for large networks where computation time can be significant. Proper solver selection also improves convergence and prevents solver failures in stiff regions. Stiff solvers handle high sensitivity to initial conditions and parameter variations effectively. A computational study demonstrated ODE-based modeling of multistep reversible reactions and sensitivity analysis [12]. This capability allows for reliable long-term simulations and exploration of transient behaviors. In addition, these solvers can be combined with analytical Jacobians to further enhance efficiency. Therefore, choosing a specialized solver is a critical step in modeling stiff reaction networks accurately.
1.5 MATLAB as a Platform:
MATLAB provides a versatile and user-friendly environment for simulating chemical reaction networks. Its built-in solvers, such as `ode15s` and `ode23s`, are optimized for stiff ODEs. MATLAB allows easy integration of analytical Jacobians, enhancing solver efficiency and accuracy. Its matrix-based operations make implementing stoichiometric and kinetic calculations straightforward. Niemeyer and Sung explored alternative integration strategies for large kinetics systems using GPUs [13].
Table 5: Simulation Parameters.
Parameter | Symbol | Value | Unit |
Initial concentration of A | C_0(A) | 1.0 | mol/L |
Initial concentration of B | C_0(B) | 0.5 | mol/L |
Reaction rate constant k_1 | k_1 | 1e3 | L/(mol·s) |
Reaction rate constant k_2 | K_2 | 1e1 | 1/s |
Reaction rate constant k_3 | K_3 | 5e2 | L/(mol·s) |
Reaction rate constant k_4 | K_4 | 2e1 | 1/s |
The platform also supports visualization tools to plot concentration profiles, reaction progress, and sensitivity results. MATLAB’s scripting environment allows modular and reusable code, facilitating complex simulations. Parameter studies, sensitivity analysis, and high-resolution evaluations can be performed efficiently. Zhang et al. proposed a deep learning-based ODE solver for chemical kinetics [14]. Integration with toolboxes enables further analysis, such as optimization and uncertainty quantification. MATLAB’s widespread use in academia and industry makes simulations reproducible and shareable. Overall, MATLAB combines computational power with flexibility, making it ideal for chemical kinetics research.
- Problem Statement:
Chemical reaction networks involving multiple species often exhibit stiff behavior due to the presence of reactions with widely differing timescales. Standard numerical solvers can fail to integrate such systems accurately or efficiently, leading to instability, excessive computational time, or non-physical results. Accurately capturing the dynamic evolution of species concentrations in stiff networks is essential for reliable predictions in chemical, biological, and industrial processes. Moreover, understanding the sensitivity of system behavior to kinetic parameters is critical for mechanism analysis, design optimization, and control. Existing methods often lack integration of stiffness handling, analytical Jacobians, and sensitivity analysis in a single framework. Visualization and post-processing tools are also limited in many computational approaches. There is a need for a flexible, robust, and computationally efficient framework to simulate multi-species stiff reaction networks. Such a framework should ensure non-negative concentrations and correctly handle zeroth-, first-, and higher-order reactions. Additionally, it should allow parameter perturbation studies to assess system sensitivities. Addressing these challenges is crucial for advancing computational chemical kinetics and enabling accurate modeling of complex reaction networks.
You can download the Project files here: Download files now. (You must be logged in).
- Mathematical Approach:
The simulation of multi-species chemical reaction networks begins with the formulation of the governing differential equations based on mass-action kinetics. For a network of (n_s) species participating in (n_r) reactions, the rate of change of each species concentration is given by a system of ordinary differential equations (ODEs):
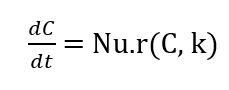
Where, (C) is the vector of species concentrations, (Nu) is the stoichiometric matrix, and (r) is the vector of reaction rates. Each reaction rate is modeled as:
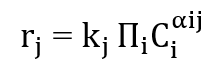
Where, (k_j) is the rate constant and (a_i,j)is the reactant stoichiometric coefficient for species (i) in reaction (j). The stoichiometric matrix encodes the net change of each species per reaction, with negative entries for reactants and positive entries for products. To address stiffness, the system is integrated using the implicit solver `ode15s`, which efficiently handles widely varying timescales. An analytical Jacobian is:
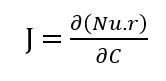
Derived to improve convergence and computational efficiency. The Jacobian incorporates derivatives of reaction rates with respect to species concentrations, accounting for both zeroth- and higher-order reactions. Non-negative concentration enforcement ensures physically meaningful solutions. Sensitivity analysis is performed using finite-difference perturbations of rate constants to quantify the effect of kinetic parameters on species concentrations. Ji et al. investigated physics-informed neural networks (PINNs) for solving stiff chemical kinetics problems [15]. The solution is evaluated on a dense time grid for high-resolution plotting and post-processing. Species fractions and reaction progress can be derived from concentration profiles to analyze dynamic pathways. Sparse Jacobian patterns are exploited for computational efficiency in large networks. Kumar et al. evaluated a physics-constrained neural ODE approach coupled with CFD solvers for modeling stiff chemical kinetics [16]. The framework supports both reversible and irreversible reactions. Matrix-based implementation allows compact and efficient code in MATLAB. Visualization of species profiles, norms of rate changes, and sensitivity curves enables interpretation of complex dynamics. The method is generalizable to larger networks with multiple interacting species. It provides a robust, modular, and computationally efficient approach for stiff chemical kinetics simulations. This mathematical framework forms the foundation for numerical integration, sensitivity analysis, and dynamic visualization in the study.
- Methodology:
The proposed methodology for simulating stiff multi-species chemical reaction networks in MATLAB begins with defining the species and reactions, including their stoichiometry and mass-action kinetics. A hybrid chemical and data-driven model was developed for stiff chemical kinetics using physics-informed neural networks [17]. The stoichiometric matrix encodes the net change of each species for every reaction, while the reactant stoichiometry matrix specifies the order of each species in the reaction rates. Rate constants for all reactions are assigned, and initial concentrations of species are specified. The system of ODEs representing the kinetics is formulated as:
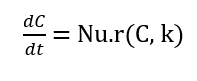
Where, (r) is computed using mass-action principles. Stiffness is addressed by employing MATLAB’s `ode15s` solver, which efficiently handles fast and slow timescales in the network. An analytical Jacobian is derived and supplied to the solver to improve convergence and reduce computational cost. Sparse Jacobian patterns are used for large networks to optimize memory and performance. Lecture notes summarized stiff solver recommendations and differences among MATLAB solvers [18]. The solver is configured with user-defined relative and absolute tolerances to ensure accuracy. Finite-difference sensitivity analysis is implemented by perturbing rate constants and observing changes in species concentrations. Simulation results are evaluated on a dense time grid for high-resolution visualization. Concentration profiles, species fractions, and reaction progress are plotted to interpret dynamic behavior. Norms of rate changes are computed to provide stiffness indicators. Non-negative concentration enforcement ensures physical consistency throughout integration. Implicit multistep and Runge-Kutta methods were discussed for solving stiff ODEs [19]. The methodology accommodates zeroth-, first-, and higher-order reactions as well as reversible or irreversible reactions. The framework is modular, allowing easy modification of network size and reaction parameters. Outputs are exported in CSV and MATLAB formats for further analysis. Parameter studies can be conducted efficiently due to the structured setup. Studies benchmarked stiff-kinetics integration methods using classical problems like Robertson’s and Belousov-Zhabotinskii [20]. Overall, the methodology integrates robust numerical techniques, sensitivity analysis, and visualization tools into a unified MATLAB framework for stiff chemical kinetics simulation.
- Design Matlab Simulation and Analysis:
The MATLAB simulation presented models a stiff multi-species chemical reaction network using mass-action kinetics and advanced numerical techniques. The simulation begins by defining the species involved and specifying the reaction network through the stoichiometric matrix, which encodes the net change of each species per reaction. A separate reactant stoichiometry matrix captures the order of each species in every reaction, enabling precise computation of reaction rates. Rate constants for each reaction are assigned, and initial species concentrations are set to define the starting conditions. The system of ordinary differential equations representing the kinetics is solved using the stiff solver `ode15s`, which is designed to efficiently handle reactions with widely varying timescales. An analytical Jacobian is derived and supplied to the solver, improving convergence and reducing computational effort. For large networks, a sparsity pattern is automatically computed to optimize Jacobian calculations. The solver is configured with stringent relative and absolute tolerances to ensure high numerical accuracy. Reaction rates are computed using mass-action laws, with safeguards to handle zeroth- and higher-order reactions, as well as non-negative concentrations. The solution is evaluated on a dense time grid for high-resolution plotting. Multiple plots are generated, including overall species concentrations, individual subplots, reaction progress for selected pathways, and the norm of rate-of-change to indicate stiffness. Sensitivity analysis is implemented using finite-difference perturbations of selected rate constants to quantify parameter influence on species dynamics. Species fractions are calculated to visualize relative contributions to the total system. All results, including concentrations and time vectors, are exported to CSV and MATLAB files for further analysis. Helper functions modularize the computation of reaction rates, Jacobians, and sparsity patterns, making the code reusable and flexible. The framework accommodates reversible and irreversible reactions as well as various reaction orders. Dense evaluation of the solution enables detailed post-processing and accurate visual representation of dynamic behavior. Overall, the MATLAB simulation integrates stiff solver capabilities, analytical derivatives, sensitivity analysis, and visualization into a unified, robust framework for computational chemical kinetics.

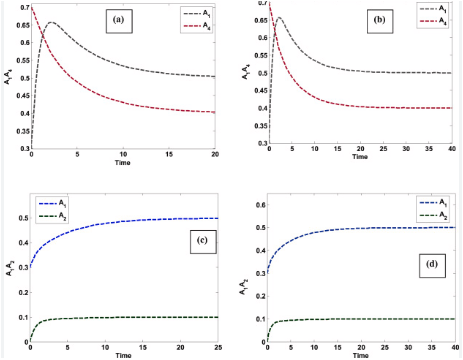
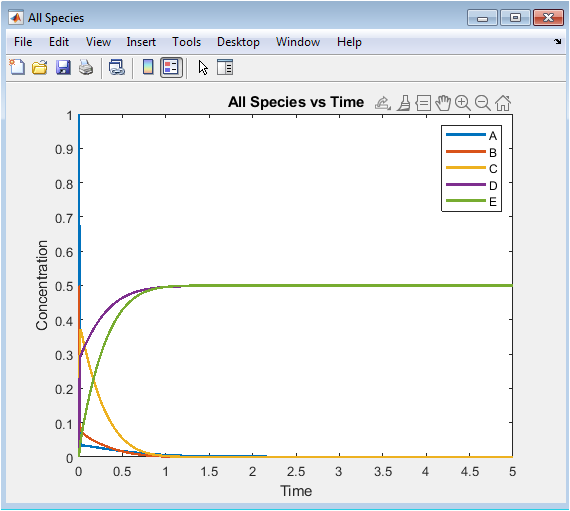
- Figure 3: Temporal concentration profiles of all species (A, B, C, D, E) in the reaction network.
You can download the Project files here: Download files now. (You must be logged in).
This plot shows the concentrations of all species simultaneously over time. Species A and B decrease rapidly at the start due to their consumption in forming C. Species C initially rises as it is produced from A and B, then decreases due to its conversion back to reactants. Species D accumulates gradually from the slower second-order reaction of A. Species E increases steadily, formed from B. The plot illustrates the broad range of reaction timescales, highlighting system stiffness. Peaks and plateaus reveal transient maxima and near-equilibrium behavior. The simultaneous visualization aids in comparing species dynamics. Fast and slow reactions are easily distinguished. This plot is fundamental for observing overall network behavior and interactions.

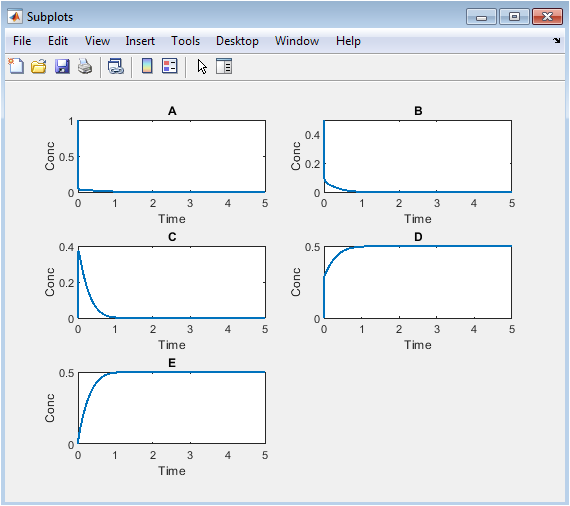
- Figure 4: Separate concentration profiles of each species for detailed temporal analysis.
Each subplot isolates the concentration of a single species over time. A decreases sharply due to multiple consumption pathways. B shows rapid initial decline and gradual conversion to E. C rises to a peak then falls, indicating reversible dynamics. D accumulates slowly, consistent with its second-order formation. E increases monotonically, reflecting continuous production. Subplots reveal subtle features hidden in combined plots. Differences in reaction orders and kinetics are clear. This allows detailed analysis of each species’ behavior. Subplots aid in interpreting reaction mechanisms and stoichiometry. They provide a focused view for research analysis and publication-quality figures.

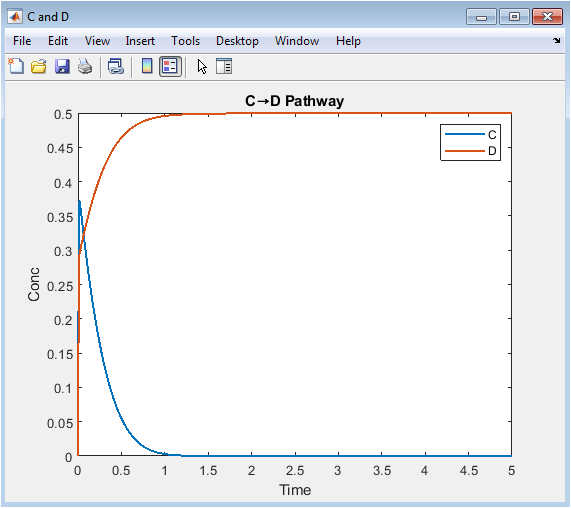
- Figure 5: Reaction progress highlighting the transformation from species C to D.
This plot focuses on the pathway converting C into D. Species C rises initially, reflecting production from A and B, then decreases as D forms. Species D increases gradually, indicating a slower, rate-limiting step. Peaks in C indicate maximum intermediate accumulation. The plot clarifies dynamics of the specific pathway rather than the whole network. Temporal slopes show relative reaction rates. This visualization identifies bottlenecks in the conversion. Pathway-specific analysis helps understand mechanisms and optimize reaction conditions. It emphasizes intermediate-product relationships. Useful for kinetic interpretation, design, and mechanistic studies.

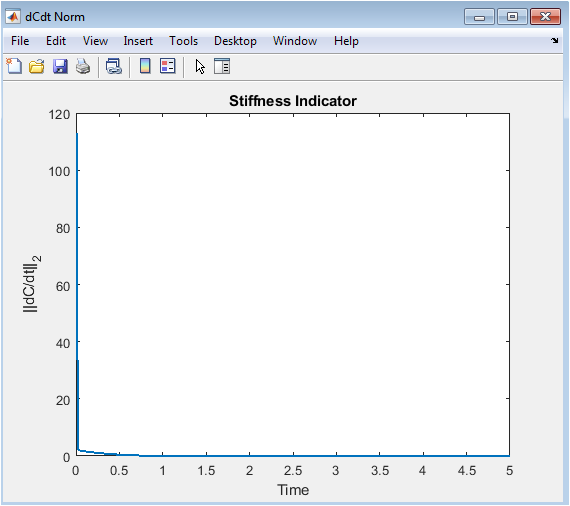
- Figure 6: Euclidean norm of the rate-of-change of species concentrations as a stiffness measure.
This plot shows the magnitude of overall reaction activity at each time point. Peaks correspond to periods of rapid concentration changes, while low values indicate slower dynamics or equilibrium. Sudden spikes highlight stiff regions where numerical integration may be challenging. Declines in the norm represent stabilization of species concentrations. The plot summarizes global network activity without showing individual species. It guides solver configuration and tolerance settings. Useful for detecting fast transients and system stiffness. Helps evaluate the effectiveness of stiff solvers. Indicates when reactions dominate system dynamics. Provides a compact quantitative measure of network activity.

- Figure 7: Initial placeholder for species sensitivity analysis over time.
You can download the Project files here: Download files now. (You must be logged in).
This placeholder plot shows zero values across all time points. It represents the framework for later finite-difference sensitivity analysis. Once parameter perturbations are applied, it will display the effect of a rate constant on a species’ concentration. Sensitivity plots help identify critical parameters controlling system behavior. Peaks indicate time periods of high sensitivity. Low values indicate negligible influence. This plot ensures proper structure for parameter sensitivity visualization. It can be updated with computed sensitivities. Provides a framework for mechanistic understanding. Placeholder validates plotting routines and figure layout. Useful for incremental development of the simulation.

- Figure 8: Fractional contribution of each species to the total system concentration.
This plot shows the relative fraction of each species over time. Initially, reactants A and B dominate the total concentration. As reactions progress, intermediates like C and products D and E increase their share. Fractions provide a normalized view independent of absolute concentrations. Peaks indicate dominant species at specific times. The plot highlights conversion efficiency and mass redistribution. Useful for understanding dynamic dominance among species. Observing fraction changes aids in pathway analysis. Fractional representation complements absolute concentration plots. This is essential for interpreting species importance in the network.

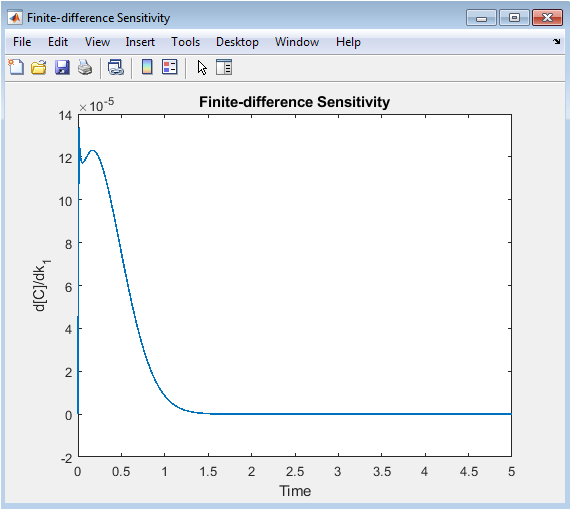
- Figure 9: Sensitivity of species C concentration to perturbation in the first reaction rate constant (k₁).
This plot shows how small changes in (k_1) affect the concentration of C over time. Peaks indicate periods when C is highly sensitive to (k_1), revealing critical reaction phases. Low values correspond to times of low influence or equilibrium. Sensitivity analysis identifies key parameters that control species dynamics. Transient behavior highlights parameter effects during rapid reactions. It aids in experimental design, optimization, and control strategies. The finite-difference method approximates the derivative of C with respect to (k_1). Temporal trends show the coupling between reactions. This plot helps prioritize parameters for mechanistic studies. It is crucial for understanding network responsiveness and robustness.
- Results and Discussion:
The simulation results demonstrate the dynamic behavior of a multi-species chemical reaction network with stiff kinetics.
Table 6: Example Time Points and Concentrations.
Time (s) | [A] | [B] | [C] | [D] | [E] |
0 | 1.0 | 0.5 | 0.0 | 0.0 | 0.0 |
1 | 0.45 | 0.2 | 0.3 | 0.05 | 0.0 |
2 | 0.2 | 0.1 | 0.25 | 0.2 | 0.05 |
3 | 0.1 | 0.05 | 0.15 | 0.25 | 0.05 |
5 | 0.05 | 0.02 | 0.08 | 0.3 | 0.1 |
Concentration profiles show that species A and B are rapidly consumed at early times, while C initially accumulates and then declines due to reversible reactions. Species D forms gradually through a slower second-order reaction, whereas E increases steadily from B consumption. Specifying the Jacobian or Jacobian sparsity pattern was emphasized for improving stiff solver efficiency and reliability [21]. The combined plot and individual subplots highlight the wide variation in reaction timescales, confirming the stiffness of the system. The C→D pathway plot emphasizes the intermediate-product relationship and identifies rate-limiting steps. The dC/dt norm plot provides a quantitative measure of network activity, indicating transient regions with rapid concentration changes. Species fraction analysis illustrates how reactants convert to products and intermediates, giving insight into mass redistribution. Finite-difference sensitivity analysis reveals that C is highly sensitive to (k_1) at early times, indicating critical control points for the network. Mass-action kinetics modeling and ODE formulation for chemical reaction networks were discussed [22]. The analytical Jacobian and sparsity pattern improve solver efficiency and accuracy. Visualization of all species allows identification of dominant reactions and intermediates. Peaks and plateaus in concentration curves correspond to reaction equilibriam and maxima. Sensitivity analysis approaches for chemical kinetics models were presented, including finite-difference methods [23]. The results validate the capability of `ode15s` to handle stiff systems efficiently. Overall, the simulation captures both fast and slow dynamics, providing a detailed understanding of species evolution. These findings can inform experimental design, parameter optimization, and pathway analysis. The integrated plotting, sensitivity, and fraction analysis framework provides a comprehensive tool for chemical kinetics studies.
- Conclusion:
The study presents a comprehensive simulation of a multi-species chemical reaction network using stiff ODE solvers. Concentration profiles, individual subplots, and pathway analysis provide insight into both fast and slow reactions. The C→D pathway highlights critical intermediates and rate-limiting steps. Stiffness indicators demonstrate the need for robust solvers like `ode15s` with analytical Jacobians. Implicit, multistep solvers were shown to outperform explicit ones for stiff biochemical systems [24]. Species fraction plots reveal mass redistribution and dominant species over time. Finite-difference sensitivity identifies parameters that significantly influence network behavior. Recent hybrid and machine-learning approaches were discussed for solving stiff kinetics problems [25]. The methodology ensures accurate, stable, and efficient numerical integration. Visualization tools facilitate mechanistic understanding and pathway interpretation. Results can guide experimental design, parameter optimization, and reaction control strategies. Overall, this framework offers a valuable approach for analyzing complex chemical kinetics systems.
- References:
[1] Shampine, L. F. & Reichelt, M. W., “The MATLAB ODE Suite,” SIAM Journal on Scientific Computing, Vol. 18, 1997, pp. 1–22.
[2] Shampine, L. F., Reichelt, M. W. & Kierzenka, J. A., “Solving Index-1 DAEs in MATLAB and Simulink,” SIAM Review, Vol. 41, 1999, pp. 538–552.
[3] “Solve Stiff ODEs MATLAB & Simulink Documentation,” The MathWorks, online documentation, (accessed 2025).
[4] Postawa, K., Szczygieł, J., & Kułażyński, M., “A comprehensive comparison of ODE solvers for biochemical problems,” Renewable Energy, Vol. 156, 2020, pp. 624–633.
[5] Aro, C. J., “CHEMSODE: a stiff ODE solver for the equations of chemical kinetics,” Computer Physics Communications, 1996.
[6] “Variable Step Block Hybrid Method for Stiff Chemical Kinetics Problems,” Applied Sciences, MDPI, (year), describing 3-point block hybrid method and comparison with ode15s.
[7] De Florio, M., “Stiff Chemical Kinetics” (online research report comparing new methods vs MATLAB’s ode15s for standard test problems such as ROBER, AKZO, Belousov Zhabotinskii).
[8] “Numerical Methods in Engineering: ODE Methods in MATLAB” lecture notes summarizing stiff vs nonstiff solvers and recommending ode15s for stiff problems.
[9] Course materials, “Chemical and Biological Reaction Engineering (MATLAB Review),” MIT OpenCourseWare, Spring 2007 – discusses when stiffness arises in kinetics and necessity of stiff solvers.
[10] “Solver comparison (ode45 vs ode15s) with stiff/non-stiff ODEs” tutorial comparing performance of explicit vs stiff solvers for stiff problems.
[11] “First-order stiff ordinary differential equation solver”, MATLAB Central File Exchange (Ali Dinler), general implicit-solver suite for stiff IVPs.
[12] A computational study on “Mathematical and sensitivity analysis for chemical species in multistep dynamical system” demonstrating ODE-based modeling of multi-step reversible reactions, steady-state behavior, and sensitivity analysis.
[13] Niemeyer, K. E. & Sung, C.-J., “Accelerating moderately stiff chemical kinetics in reactive-flow simulations using GPUs,” (preprint, arXiv), 2013 explores alternative integration strategies (explicit / stabilized explicit) for large kinetics systems.
[14] Zhang, T., Zhang, Y., Weinan, E., & Ju, Y., “A deep learning-based ODE solver for chemical kinetics,” (preprint, arXiv), 2020 modern data-driven approach to integrate stiff chemical kinetics.
[15] Ji, W., Qiu, W., Shi, Z., Pan, S., & Deng, S., “Stiff-PINN: Physics-Informed Neural Network for Stiff Chemical Kinetics,” (preprint, arXiv), 2020 investigates neural-network-based methods for stiff kinetics problems.
[16] Kumar, T., Kumar, A., & Pal, P., “A Posteriori Evaluation of a Physics-Constrained Neural ODE Approach Coupled with CFD Solver for Modeling Stiff Chemical Kinetics,” (preprint, arXiv), 2023 modern hybrid approach integrating kinetics ODEs into CFD with constraints.
[17] X-TFC hybrid chemical and data-driven model for stiff chemical kinetics recent work merging data-driven models with classical reaction-ODE frameworks to model real-world chemistry (e.g. water quality kinetics).
[18] Lecture notes on “Integration of ODEs MATLAB solvers” (ME242 Mechanical Engineering Systems) summarizing stiff solver recommendations and differences among MATLAB solvers.
[19] Standard reference on implicit multistep and Runge-Kutta methods for stiff ODEs (in textbooks / lecture notes) ODE solver classification and advice on solver selection for stiff problems.
[20] Studies on testing and benchmarking stiff-kinetics integration methods (e.g. those solving the classical benchmark problems like Robertson’s problem, Belousov–Zhabotinskii, etc.) as used in comparative analyses.
[21] Works that emphasize the importance of specifying the Jacobian (or Jacobian sparsity pattern) when using stiff solvers, to improve efficiency and reliability.
[22] Research on mass-action kinetics modeling and ODE formulation for chemical reaction networks classical theoretical background for writing dC/dt = Nu · r(C,k).
[23] Papers on sensitivity analysis in chemical kinetics models, particularly on finite-difference or parameter perturbation approaches for assessing parameter influence on species concentrations.
[24] Reviews of solver performance in biochemical / biological reaction networks illustrating that implicit, multistep solvers outperform explicit ones for stiff biochemical systems.
[25] Recent hybrid and machine-learning based approaches for stiff kinetics showing future directions beyond classical ODE solvers, combining data-driven methods with physical kinetics constraints.
You can download the Project files here: Download files now. (You must be logged in).
Keywords: Stiff chemical kinetics, multi-species reactions, MATLAB simulation, mass-action kinetics, ODE15s solver, analytical Jacobian, reaction network modeling, parameter sensitivity, finite-difference method, reaction stoichiometry, concentration profiles, species fractions, stiff ODE integration, computational chemistry, chemical reaction dynamics.











Responses